浅入浅出 Java 排序算法

• 2019 年 10 月 3 日
• 筆記

Java String 源码的排序算法

一、前言

Q：什么是选择问题？
选择问题，是假设一组 N 个数，要确定其中第 K 个最大值者。比如 A 与 B 对象需要哪个更大？又比如：要考虑从一些数组中找出最大项？

解决选择问题，需要对象有个能力，即比较任意两个对象，并确定哪个大，哪个小或者相等。找出最大项问题的解决方法，只要依次用对象的比较（Comparable）能力，循环对象列表，一次就能解决。

那么 JDK 源码如何实现比较（Comparable）能力的呢？

二、java.lang.Comparable 接口

Comparable 接口，从 JDK 1.2 版本就有了，历史算悠久。Comparable 接口强制了实现类对象列表的排序。其排序称为自然顺序，其 compareTo 方法，称为自然比较法。

该接口只有一个方法 public int compareTo(T o); ，可以看出

• 入参 T o ：实现该接口类，传入对应的要被比较的对象
• 返回值 int：正数、负数和 0 ，代表大于、小于和等于

对象的集合列表（Collection List）或者数组（arrays） ，也有对应的工具类可以方便的使用：

• java.util.Collections#sort(List) 列表排序
• java.util.Arrays#sort(Object[]) 数组排序

那 String 对象如何被比较的？

三、String 源码中的算法

String 源码中可以看到 String JDK 1.0 就有了。那么应该是 JDK 1.2 的时候，String 类实现了 Comparable 接口，并且传入需要被比较的对象是 String。对象如图：

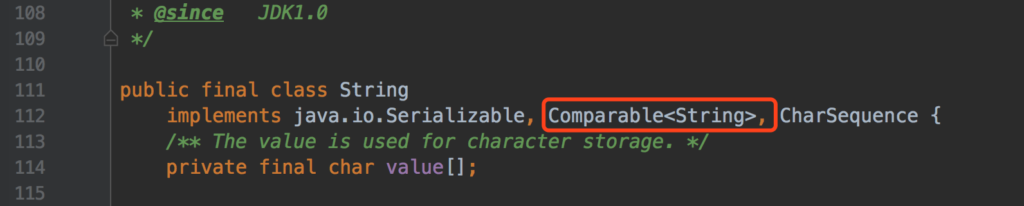
String 是一个 final 类，无法从 String 扩展新的类。从 114 行，可以看出字符串的存储结构是字符（Char）数组。先可以看看一个字符串比较案例，代码如下：

  /**   * 字符串比较案例   *   * Created by bysocket on 19/5/10.   */  public class StringComparisonDemo {        public static void main(String[] args) {          String foo = "ABC";            // 前面和后面每个字符完全一样，返回 0          String bar01 = "ABC";          System.out.println(foo.compareTo(bar01));            // 前面每个字符完全一样，返回：后面就是字符串长度差          String bar02 = "ABCD";          String bar03 = "ABCDE";          System.out.println(foo.compareTo(bar02)); // -1 (前面相等,foo 长度小 1)          System.out.println(foo.compareTo(bar03)); // -2 (前面相等,foo 长度小 2)            // 前面每个字符不完全一样，返回：出现不一样的字符 ASCII 差          String bar04 = "ABD";          String bar05 = "aABCD";          System.out.println(foo.compareTo(bar04)); // -1  (foo 的 'C' 字符 ASCII 码值为 67，bar04 的 'D' 字符 ASCII 码值为 68。返回 67 - 68 = -1)          System.out.println(foo.compareTo(bar05)); // -32 (foo 的 'A' 字符 ASCII 码值为 65，bar04 的 'a' 字符 ASCII 码值为 97。返回 65 - 97 = -32)            String bysocket01 = "泥瓦匠";          String bysocket02 = "瓦匠";          System.out.println(bysocket01.compareTo(bysocket02));// -2049 （泥 和 瓦的 Unicode 差值）      }  }  

运行结果如下：

0  -1  -2  -1  -32  -2049  

可以看出， compareTo 方法是按字典顺序比较两个字符串。具体比较规则可以看代码注释。比较规则如下：

• 字符串的每个字符完全一样，返回 0
• 字符串前面部分的每个字符完全一样，返回：后面就是两个字符串长度差
• 字符串前面部分的每个字符存在不一样，返回：出现不一样的字符 ASCII 码的差值
  • 中文比较返回对应的 Unicode 编码值（Unicode 包含 ASCII）
  • foo 的 ‘C’ 字符 ASCII 码值为 67
  • bar04 的 ‘D’ 字符 ASCII 码值为 68。
  • foo.compareTo(bar04)，返回 67 – 68 = -1
  • 常见字符 ASCII 码，如图所示

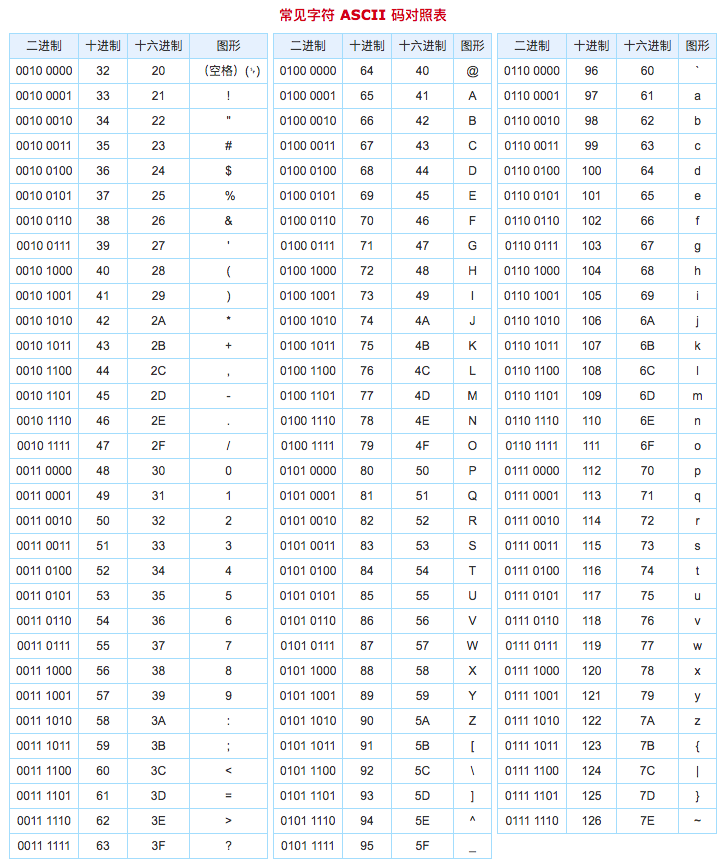
再看看 String 的 compareTo 方法如何实现字典顺序的。源码如图：

源码解析如下：

• 第 1156 行：获取当前字符串和另一个字符串，长度较小的长度值 lim
• 第 1161 行：如果 lim 大于 0 （较小的字符串非空），则开始比较
• 第 1164 行：当前字符串和另一个字符串，依次字符比较。如果不相等，则返回两字符的 Unicode 编码值的差值
• 第 1169 行：当前字符串和另一个字符串，依次字符比较。如果均相等，则返回两个字符串长度的差值

所以要排序，肯定先有比较能力，即实现 Comparable 接口。然后实现此接口的对象列表（和数组）可以通过 Collections.sort（和 Arrays.sort）进行排序。

还有 TreeSet 使用树结构实现（红黑树），集合中的元素进行排序。其中排序就是实现 Comparable 此接口

另外，如果没有实现 Comparable 接口，使用排序时，会抛出 java.lang.ClassCastException 异常。详细看《Java 集合：三、HashSet，TreeSet 和 LinkedHashSet比较》https://www.bysocket.com/archives/195

四、小结

上面也说到，这种比较其实有一定的弊端：

• 默认 compareTo 不忽略字符大小写。如果需要忽略，则重新自定义 compareTo 方法
• 无法进行二维的比较决策。比如判断 2 * 1 矩形和 3 * 3 矩形，哪个更大？
• 比如有些类无法实现该接口。一个 final 类，也无法扩展新的类。其也有解决方案：函数对象（Function Object）

方法参数：定义一个没有数据只有方法的类，并传递该类的实例。一个函数通过将其放在一个对象内部而被传递。这种对象通常叫做函数对象（Funtion Object）

在接口方法设计中， T execute(Callback callback) 参数中使用 callback 类似。比如在 Spring 源码中，可以看出很多设计是：聚合优先于继承或者实现。这样可以减少很多继承或者实现。类似 SpringJdbcTemplate 场景设计，可以考虑到这种 Callback 设计实现。

那插入排序呢？

文章工程：

• JDK 1.8
• 工程名：algorithm-core-learning
• 工程地址：https://github.com/JeffLi1993/algorithm-core-learning

一、前言

上面 Java String 源码的排序算法，讲了什么是选择问题，什么是比较能力。

选择问题，是假设一组 N 个数，要确定其中第 K 个最大值者。算法是为求解一个问题。

那什么是算法？
算法是某种集合，是简单指令的集合，是被指定的简单指令集合。确定该算法重要的指标：

• 第一是否能解决问题；
• 第二算法运行时间，即解决问题出结果需要多少时间；
• 还有所需的空间资源，比如内存等。

很多时候，写一个工作程序并不够。因为遇到大数据下，运行时间就是一个重要的问题。

算法性能用大 O 标记法表示。大 O 标记法是标记相对增长率，精度是粗糙的。比如 2N 和 3N + 2 ，都是 O(N)。也就是常说的线性增长，还有常说的指数增长等

典型的增长率

典型的提供性能做法是分治法，即分支 divide and conquer 策略：

1. 将问题分成两个大致相等的子问题，递归地对它们求解，这是分的部分；
2. 治阶段将两个子问题的解修补到一起，并可能再做些少量的附加工作，最后得到整个问题的解。

二、排序

排序问题，是古老，但一直流行的问题。从 ACM 接触到现在工作，每次涉及算法，或品读 JDK 源码中一些算法，经常会有排序的算法出现。

排序算法是为了将一组数组（或序列）重新排列，排列后数据符合从大到小（或从小到大）的次序。这样数据从无序到有序，会有什么好处？

• 应用层面：解决问题。
  • 最简单的是可以找到最大值或者最小值
  • 解决"一起性"问题，即相同标志元素连在一起
  • 匹配在两个或者更多个文件中的项目
  • 通过键码值查找信息
• 系统层面：减少系统的熵值，增加系统的有序度
  （Donald Knuth 的经典之作《计算机程序设计艺术》(The Art of Computer Programming)的第三卷）

通过维基百科查阅资料得到：
在主内存中完成的排序叫做，内部排序。那需要在磁盘等其他存储完成的排序，叫做外部排序 external sorting。资料地址：https://en.wikipedia.org/wiki/External_sorting

上一篇《Java String 源码的排序算法》，讲到了 java.lang.Comparable 接口。那么接口是一个抽象类型，是抽象方法（compareTo）的集合，用 interface 来声明。因此被排序的对象属于 Comparable 类型，即实现 Comparable 接口，然后调用对象实现的 compareTo 方法进行比较后排序。

在这些条件下的排序，叫作基于比较的排序（comparison-based sorting）

三、插入排序

白话文：熊大（一）、熊二、熊三… 按照身高从低到高排队（排序）。这时候熊 N 加入队伍，它从队伍尾巴开始比较。如果它比前面的熊身高低，则与被比较的交换位置，依次从尾巴到头部进行比较 & 交换位置。最终换到了应该熊 N 所在的位置。这就是插入排序的原理。

插入排序（insertion sort）

• 最简单的排序之一。ps: 冒泡排序看看就好，不推荐学习
• 由 N – 1 次排序过程组成。
  • 如果被排序的这样一个元素，就不需要排序。即 N =1 （1 – 1 = 0）
  • 每一次排序保证，从第一个位置到当前位置的元素为已排序状态。
• 如图：每个元素往前进行比较，并终止于自己所在的位置

/**   * 插入排序案例   * <p>   * Created by 泥瓦匠@bysocket.com on 19/5/15.   */  public class InsertionSortingDemo {        /**       * 插入排序       *       * @param arr 能比较的对象数组       * @param <T> 已排序的对象数组       */      public static <T extends Comparable> void insertionSort(T[] arr) {          int j;            // 从数组第二个元素开始，向前比较          for (int p = 1; p < arr.length; p++) {              T tmp = arr[p];              // 循环，向前依次比较              // 如果比前面元素小，交换位置              for (j = p; (j > 0) && (tmp.compareTo(arr[j - 1]) < 0); j--) {                  arr[j] = arr[j - 1];              }              // 如果比前面元素大或者相等，那么这就是元素的位置，交换              arr[j] = tmp;          }      }        public static void main(String[] args) {          Integer[] intArr = new Integer[] {2, 3, 1, 4, 3};            System.out.println(Arrays.toString(intArr));          insertionSort(intArr);          System.out.println(Arrays.toString(intArr));      }  }

代码解析如下：

• 从数组的第二个元素，向前开始比较。比第一个元素小，则交换位置
• 如果第二个元素比较完毕，那就第三个，第四个… 以此类推
• 比较到最后一个元素时，完成排序

时间复杂度是 O(N^2)，最好情景的是排序已经排好的，那就是 O（N），因为满足不了循环的判断条件；最极端的是反序的数组，那就是 O(N^2)。所以该算法的时间复杂度为 O(N^2)

运行 main 方法，结果如下：

[2, 3, 1, 4, 3]  [1, 2, 3, 3, 4]

再考虑考虑优化，会怎么优化呢？
插入排序优化版 不是往前比较 。往前的一半比较，二分比较会更好。具体代码，可以自行试试

四、Array.sort 源码中的插入排序

上面用自己实现的插入算法进行排序，其实 JDK 提供了 Array.sort 方法，方便排序。案例代码如下：

/**   * Arrays.sort 排序案例   * <p>   * Created by 泥瓦匠@bysocket.com on 19/5/28.   */  public class ArraysSortDemo {        public static void main(String[] args) {            Integer[] intArr = new Integer[] {2, 3, 1, 4, 3};            System.out.println(Arrays.toString(intArr));          Arrays.sort(intArr);          System.out.println(Arrays.toString(intArr));      }  }

运行 main 方法，结果如下：

[2, 3, 1, 4, 3]  [1, 2, 3, 3, 4]

那 Arrays.sort 是如何实现的呢？JDK 1.2 的时候有了 Arrays ，JDK 1.8 时优化了一版 sort 算法。大致如下：

• 如果元素数量小于 47，使用插入排序
• 如果元素数量小于 286，使用快速排序
• Timsort 算法整合了归并排序和插入排序

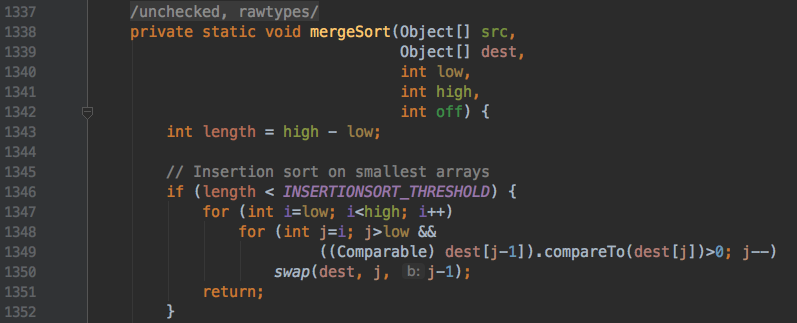
源码中我们看到了 mergeSort 里面整合了插入排序算法，跟上面实现的异曲同工。这边就不一行一行解释了。

五、小结

算法是解决问题的。所以不一定一个算法解决一个问题，可能多个算法一起解决一个问题。达到问题的最优解。插入排序，这样就这么简单

代码示例

本文示例读者可以通过查看下面仓库的中: StringComparisonDemo 字符串比较案例案例：

• Github：https://github.com/JeffLi1993/algorithm-core-learning
• Gitee：https://gitee.com/jeff1993/algorithm-core-learning

参考资料

• 《数据结构与算法分析：Java语言描述（原书第3版）》
• https://en.wikipedia.org/wiki/Unicode
• https://www.cnblogs.com/vamei/tag/%E7%AE%97%E6%B3%95/
• https://www.bysocket.com/archives/2314/algorithm