後綴自動機(SAM)+廣義後綴自動機(GSA)
經過一頓操作之後竟然疑似沒退役0 0
你是XCPC選手嗎?我覺得我是!
稍微補一點之前丟給隊友的知識吧,除了數論以外都可以看看,為Dhaka和新隊伍做點準備…
不錯的零基礎教程見 IO WIKI – 後綴自動機,這篇就從自己的角度總結一下吧,感覺思路總是和別人不一樣…盡量用我比較能接受的語言和邏輯重新組織一遍。
注意:在本文中,字元串的下標從1開始。
目前的 SAM 模板:


const int N=100005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(char),並使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }sam;
View Code
目前的 GSA 模板:


typedef pair<int,int> pii; const int N=1000005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct GeneralSuffixAutomaton { int sz; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(int,char) GeneralSuffixAutomaton() { len[0]=0,link[0]=-1; sz=0; } //向trie樹上插入一個字元串 void insert(char *s,int n) { for(int i=1,cur=0;i<=n;i++) { int c=s[i]-'a'; if(!nxt[cur][c]) nxt[cur][c]=++sz; cur=nxt[cur][c]; } } //擴展GSA,對於lst的c轉移進行擴展 int extend(int lst,int c) { int cur=nxt[lst][c]; len[cur]=len[lst]+1; int p=link[lst]; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; for(int i=0;i<C;i++) nxt[clone][i]=len[nxt[q][i]]?nxt[q][i]:0; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } return cur; } //基於trie樹建立GSA void build() { queue<pii> Q; for(int i=0;i<C;i++) if(nxt[0][i]) Q.push(pii(0,i)); while(!Q.empty()) { pii tmp=Q.front(); Q.pop(); int cur=extend(tmp.first,tmp.second); for(int i=0;i<C;i++) if(nxt[cur][i]) Q.push(pii(cur,i)); } } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }gsa;
View Code
簡單的目錄:
正確性證明(其實沒寫啥…)
~ 背景 ~ (SAM 要解決什麼問題,為什麼「暴力」方法不行)
很久以前就聽說過 SAM,一直有一個不明覺厲的印象,導致一直沒敢看。但其實 SAM 本質上來說是一個偏板子的知識點(甚至板子也不算長),其中比較困難的地方在於對於 SAM 結構的理解,以及再次基礎上對於其性質的利用。網路上的各種材料,感覺大多從一個已經有一定理解的角度來進行講述,一開始看下來感覺有點概念不清晰。
簡單來說,SAM 想要解決的是一個這樣的問題:首先對於字元串 $s$ 建立一個自動機,再將另外的字元串$t$扔到自動機裡面逐字元進行匹配。假設目前已經匹配到了 $t[i]$,那麼這個匹配到的狀態表示的意思是「$t[1:i]$ 的 $i$ 個後綴中,最長的出現在 $s$ 中的連續子字元串」。
舉個例子,$s=abb$、$t=abbcab$,那麼匹配到 $t[6]=b$ 時,匹配到的狀態應該是 $ab$。雖然 $s$ 與 $t$ 的最長公共連續子字元串為 $abb$,但是因為 $abb$ 不是 $t[1:6]$ 的後綴,所以不是需要求的結果。
對於這個問題有一種非常暴力的做法,就是用 $s$ 的 $\dfrac{|s|\cdot (|s|-1)}{2}$ 個子串來建立 AC 自動機。在這個自動機上我們能夠匹配到 $s$ 的任意連續子字元串,於是能夠滿足我們的需求,但是狀態數直接爆炸了。我們需要一個類似這個 AC 自動機的結構(包含狀態、轉移邊和 fail 邊的自動機,通過轉移邊進行一次匹配,失配的時候通過 fail 邊往回跳),但是狀態數是 $O(|s|)$ 的。
~ 概念:endpos 等價類 ~ (規定一種將多個子串歸入到同一個狀態的規則)
為了將狀態由 $O(|s|^2)$ 壓縮到 $O(|s|)$,我們需要一個狀態能夠表示多個 $s$ 的子串。我們規定,若兩個 $s$ 的子串 endpos 等價,則其屬於同一個 SAM 狀態。
那麼我們首先需要了解 endpos 的概念。對於子串 $s’\in s$,其 endpos 等於其出現在 $s$ 中的右端位置的集合。舉個例子來說,$s=abcabbacab$、$s’=ab$,我們可以通過肉眼發現 $s’$ 在 $s$ 中出現的位置有$[1:2]$、$[4:5]$、$[9:10]$,那麼有 $\mathrm{endpos}(s’)=\{2,5,10\}$。需要注意的是,$s’$ 在 $s$ 中出現的位置可能重疊,比如$s=aaaa$、$s’=aa$,那麼 $s’$ 的出現位置為$[1:2]$、$[2:3]$、$[3:4]$,此時 $\mathrm{endpos}(s’)=\{2,3,4\}$。
對於兩個 $s$ 的子串$s_1’$、$s_2’$,如果有 $\mathrm{endpos}(s_1′)=\mathrm{endpos}(s_2′)$,那麼我們稱 $s_1’$ 與 $s_2’$ endpos 等價,其屬於同一個 endpos 等價類。
下面以字元串 $s=abab$ 為例,對於其所有子串進行等價類劃分:
| 子串 | endpos | 子串 | endpos |
| abab | $\{4\}$ | ba | $\{3\}$ |
| aba | $\{3\}$ | a | $\{1,3\}$ |
| bab | $\{4\}$ | b | $\{2,4\}$ |
| ab | $\{2,4\}$ | $\empty$ | / |
根據上表,一共可以劃分出 $5$ 個等價類:$\mathrm{endpos}(ba,aba)=\{3\}$,$\mathrm{endpos}(bab,abab)=\{4\}$,$\mathrm{endpos}(a)=\{1,3\}$,$\mathrm{endpos}(b,ab)=\{2,4\}$,以及需要單列出來的空串 $\empty$(我們可以認為 $\mathrm{endpos}(\empty)=\{0,1,2,\cdots,|s|\}$,包含 $0$ 是為了區分形如 $s=aa\cdots a$ 時的 $\mathrm{endpos}(a)$)。
~ 概念:SAM 的狀態 ~ (同一 / 不同狀態中的子串具有什麼性質與聯繫,這對於理解建立 SAM 的過程十分關鍵)
有了 endpos 等價類的定義,我們考慮屬於同一等價類的子串具有什麼樣的性質。
首先,假如兩個子串 $s_1’$ 與 $s_2’$ 具有相同的 $\mathrm{endpos}$,考慮一個具體的出現位置 $r\in \mathrm{endpos}$ 則有 $s_1’=s[l_1:r]$、$s_2’=s[l_2:r]$,那麼顯然兩者必須存在後綴關係。
接著,我們考慮字元串 $s$ 的兩個子串 $s_{long}’$ 與 $s_{short}’$,其中 $s_{short}’$ 是 $s_{long}’$ 的一個後綴。對於這兩個子串的 endpos,顯然每個 $s_{long}’$ 出現的位置上均出現了$s_{short}’$,這也就是說有:
\[\mathrm{endpos}(s_{long}’)\subseteq \mathrm{endpos}(s_{short}’)\]
這個式子說明,對於某個子串 $s’$ 的所有後綴,其 $\mathrm{endpos}$ 集合的大小隨著後綴長度的增加而單調不增,那麼屬於同一狀態(即 endpos 相同)的所有子串應該是一些長度連續的、互為後綴的字元串。【這裡說實話有點繞,需要努力理解一下】
引用 OI WIKI 的表述,也許能更好的幫助理解 「長度連續、互為後綴」:
對於每一個狀態 $v$,一個或多個子串與之匹配。我們記 $longest(v)$ 為其中最長的一個字元串,記 $len(v)$ 為它的長度。類似地,記 $shortest(v)$ 為最短的子串,它的長度為 $minlen(v)$。那麼對應這個狀態的所有字元串都是字元串 $longest(v)$ 的不同的後綴,且所有字元串的長度恰好覆蓋區間 $[minlen(v), len(v)]$ 中的每一個整數。
舉一個例子,假如字元串為 ababcabcd,那麼集合劃分如下,可以驗證一下上述性質:
| 字元串 | endpos | 字元串 | endpos | 字元串 | endpos |
| a | $\{1,4\}$ | c | $\{3,6\}$ | ca | $\{4\}$ |
| b | $\{2,5\}$ | bc | bca | ||
| ab | abc | abca | |||
| cab | $\{5\}$ | cabc | $\{6\}$ | ||
| bcab | bcabc | ||||
| abcab | abcabc | ||||
雖然在實際中我們並不會存下一個 SAM 狀態中的全部字元串,但暫時可以將每個狀態形象地理解成 endpos 等價的的字元串集合,從而幫助理解建立 SAM 的過程。
從自動機匹配的角度來看的話,如果我們在 SAM 上匹配到了某一狀態,這就表示自動機接受了這個字元串集合中的其中一個字元串(其實我們有辦法確定具體是哪一個,但要等到學完怎麼建 SAM 後才能說清楚)。
~ 概念:後綴鏈接 link ~ (SAM 中的 「fail」 轉移邊)
除了狀態以外,自動機的另一個重要的組成部分就是轉移。與 AC 自動機十分相似的是,後綴自動機也有 $\mathrm{nxt}$(匹配成功時)與 $\mathrm{link}$(匹配失敗時,對應著 AC 自動機中的 $\mathrm{fail}$)兩類轉移。其中 $\mathrm{nxt}$ 的意義與 AC 自動機中的 $\mathrm{nxt}$ 完全一致,就不做展開了;需要稍微解釋一下的是後綴鏈接 $\mathrm{link}$。
後綴鏈接的定義為:對於 SAM 中的一個狀態 $state$,其對應 endpos 等價類中的字元串均為 $\mathrm{longest}(state)$ 的後綴(這是之前的結論);我們取一個最長的 $\mathrm{longest}(state)$ 的後綴,使得其與 $\mathrm{longest}(state)$ 不 endpos 等價(其實這個後綴就是 $\mathrm{shortest}(state)$ 再去掉最左邊的一個字元,長度為 $\mathrm{minlen}(state)-1$),我們就將這個最長後綴所在的狀態賦給 $\mathrm{link}(state)$。於是我們得到一個挺常用的性質:
\[\mathrm{minlen}(state)=\mathrm{len}\left(\mathrm{link}(state)\right)+1\]
根據上述定義,我們可以對上面的例子得到後綴鏈接(紅色箭頭):

我們嘗試理解一下為什麼失配時要跳後綴鏈接。對於當前已匹配到的狀態 $state$,有$\mathrm{endpos}(state)=\{p_1, p_2,\cdots, p_n\}$,那麼在狀態 $state$ 嘗試匹配字元 $c$ 失配,就表示 $s[p_1+1], s[p_2+1], \cdots, s[p_n+1]$ 均不等於 $c$(否則就存在 $\mathrm{nxt}(c)$ 的轉移邊),那麼我們就需要捨棄一部分已匹配串的前綴(即取已匹配串的一個後綴)後再次嘗試匹配。當我們通過後綴鏈接跳到 $\mathrm{link}(state)$ 時,這個狀態的 endpos 集合更大了一些,我們說不定能找到某個新增的 $p_i$ 使得 $s[p_i+1]=c$,從而完成匹配。從這個角度來看,轉移到 $\mathrm{link}(state)$ 時我們只需要捨棄最小的已匹配長度,就會帶來 endpos 集合的變大,而 endpos 集合的變大則有可能新增一些 $\mathrm{nxt}$ 轉移使得待匹配的字元 $c$ 被接受,這個邏輯和 AC 自動機的 $\mathrm{fail}$ 邊是完全一致的。
SAM 的建立是一個在線的過程。假如我們需要對於字元串 $s$ 構建 SAM,我們依次往 SAM 中添加每一個字元 $s[i]$ 來將 SAM 進行一次擴展,接下來細說一次擴展中需要做的事情。
首先,在未添加任何字元時,有一個初始狀態對應著空集 $\empty$ 的等價類,我們將其記作 $state_0$。
在進行擴展的過程中,我們維護了一個變數:$last$。其表示在擴展字元 $s[i]$ 之前,字元串 $s[1:i-1]$ 在部分建成的 SAM 中所屬的狀態。初始時 $last=state_0$。
接下來,我們嘗試在當前串 $s[1:i-1]$ 的後面再插入一個字元 $s[i]=c$。我們首先創建一個新的節點 $cur$,並賦值 $\mathrm{len}(cur)=\mathrm{len}(last)+1$,此時 $last$ 的轉移邊及 $\mathrm{link}(cur)$ 仍未確定,需要進行如下的討論:
1. 我們從 $last$ 開始,沿著後綴鏈接 $\mathrm{link}$ 一直走,邊走邊將途徑節點(包含 $last$)的 $\mathrm{nxt}(c)$ 均賦值為 $cur$,直到某個節點 $p$ 存在 $\mathrm{nxt}(c)$ 的轉移邊才停下。假如這樣的節點 $p$ 不存在,那麼我們會一直走到 $state_0$,此時我們直接令 $\mathrm{link}(cur)=state_0$ 即可完成操作。

2. 假如我們在一個節點 $p$ 停下,那麼我們記 $p$ 通過字元 $c$ 轉移到的節點為 $q$,即有 $\mathrm{nxt}_p(c)=q$。現在考慮 $\mathrm{len}(p)$ 與 $\mathrm{len}(q)$ 之間的關係。假如 $\mathrm{len}(p)+1=\mathrm{len}(q)$ 成立,那麼我們僅需令 $\mathrm{link}(cur)=q$ 即可完成操作。
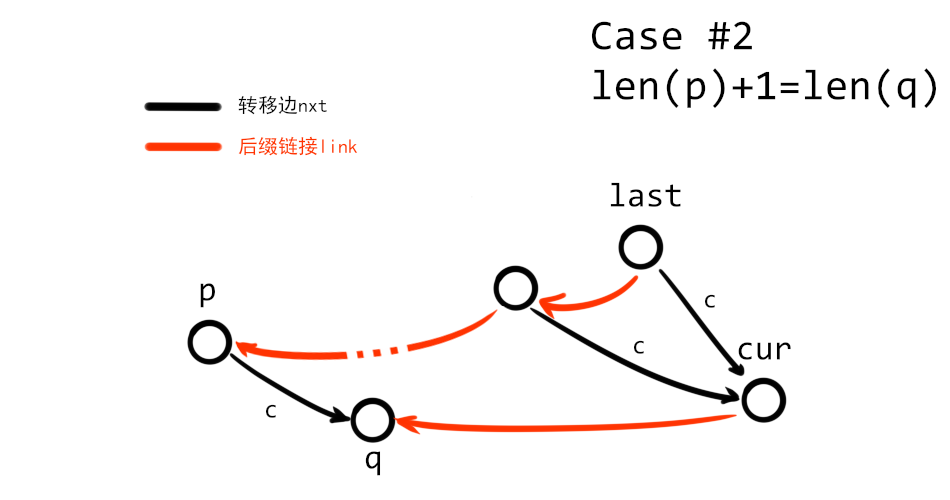
3. 假如有 $\mathrm{len}(p)+1\neq \mathrm{len}(q)$,那麼需要通過依次通過四步來擴展 SAM:
(1) 新建一個節點 $clone$,設定 $\mathrm{len}(clone)=\mathrm{len}(p)+1$,並複製 $q$ 的所有 $\mathrm{nxt}$ 轉移。例如,假如有 $\mathrm{nxt}_q(c)=tmp$,就同樣令 $\mathrm{nxt}_{clone}(c)=tmp$;
(2) 同樣是對於 $clone$,複製 $q$ 的後綴鏈接(即令 $\mathrm{link}(clone)=\mathrm{link}(q)$),同時抹去 $\mathrm{link}(q)$;
(3) 從 $p$ 開始(包含 $p$)沿著後綴鏈接 $\mathrm{link}$ 一直走到 $state_0$。假設在這個過程中經過某個節點 $x$,且存在 $\mathrm{nxt}_x(c)=q$ 的轉移,就將該轉移重定向至 $clone$(即令 $\mathrm{nxt}_x(c)=clone$);
(4) 將 $q$ 和 $cur$ 的後綴鏈接指向 $clone$,即令 $\mathrm{link}(q)=\mathrm{link}(cur)=clone$。
做完以上四步以後,最麻煩的 $\mathrm{len}(p)+1\neq \mathrm{len}(q)$ 的 case 也已經解決了。
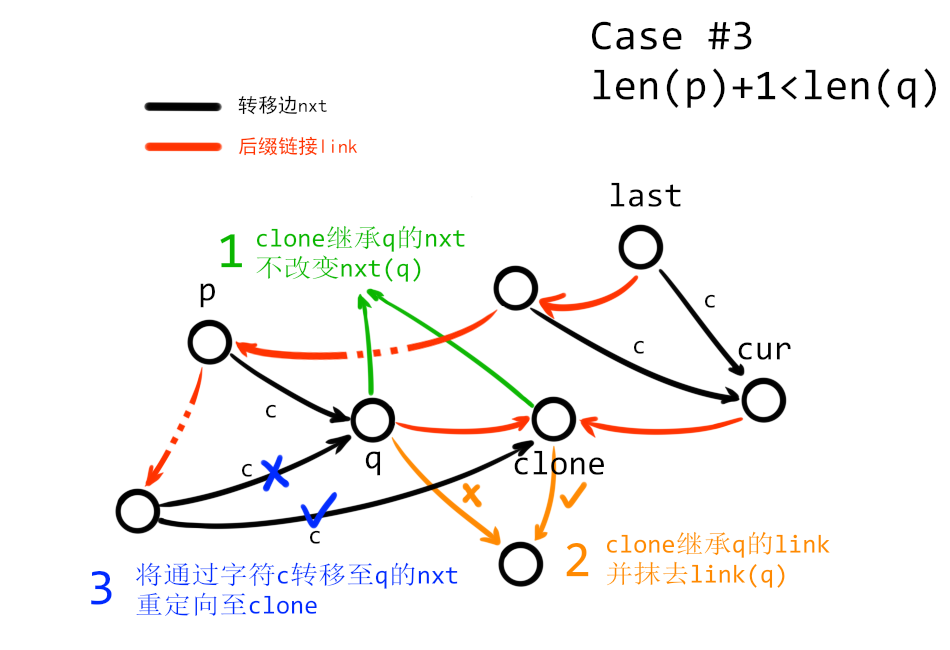
(上圖中實際上節點 $p$ 也是需要重定向的,但為了表示的方便,沒有畫出重定向 $\mathrm{nxt}_p(c)$ 的箭頭)
最後的最後,我們令 $last=cur$,為擴展下一個字元做準備。
雖然說了那麼多,其實程式碼實現相當簡單,與上面的討論一一對應,甚至沒有什麼注釋的必要:
int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //初始情況下,sz=lst=0,len[0]=0,link[0]=-1 //令link[0]=-1是為了標記後綴鏈接路徑的終點 void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) //case #1 link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) //case #2 link[cur]=q; else { //case #3 int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; }
細節有點多(懶),具體可以參考 OI WIKI – SAM – 正確性證明 以及 OI WIKI – SAM – 對操作數為線性的證明。不過對於抄板子不是那麼關鍵。
為了便於感性的理解,我們不妨舉一個擴展 SAM 的過程中最複雜的 Case #3 的例子。
字元串 $s=abb$,當僅擴展了 $ab$ 與擴展完了 $abb$ 時,SAM 的結構分別如下:

可以看出,做一次 Case #3 的擴展相當於對於一個 endpos 等價類(如圖中的 $\{b,ab\}$)做拆分。更深入的分析就不展開了。
對於一個長度為 $n$ 的字元串,SAM 的狀態數是 $2n$ 級別的,轉移數是 $3n$ 級別的。這個性質沒什麼特殊的應用,記得數組別開小就行了。
比較關鍵的性質在於 SAM 的後綴鏈接 $\mathrm{link}$ 上。
1. SAM 的後綴鏈接構成一個樹形結構
我們不妨回顧一下後綴鏈接的定義:對於 SAM 中的一個狀態 $state$,我們取一個最長的 $\mathrm{longest}(state)$ 的後綴,使得其與 $\mathrm{longest}(state)$ 不 endpos 等價,$\mathrm{link}(state)$ 就指向該後綴所屬於的狀態。
這也就是說,對於任意狀態 $state$ 的後綴鏈接所指向的狀態 $\mathrm{link}(state)$,$state$ 所包含的子串長度均長於 $\mathrm{link}(state)$ 中的子串長度(即 $\mathrm{minlen}(state)>\mathrm{len}(\mathrm{link}(state))$)。利用這個性質,我們發現後綴鏈接不會構成環,因為沿著後綴鏈接走時,所經過狀態中的子串長度嚴格單調減。
同時,由於所有後綴鏈接的路徑一定止於 $state_0$,所以所有後綴鏈接一定構成樹形結構。有說法稱其為 parent 樹。
2. 在 parent 樹上,祖先對應的字元串是子孫的後綴
上文已經回答過了,「沿著後綴鏈接走時,所經過狀態中的子串長度嚴格單調減」。
稍微推廣一下,我們可以求出多個字元串的最長公共後綴:對於字元串 $s_1,\cdots,s_n$,我們找到其在 SAM 上的位置 $x_1,\cdots,x_n$,那麼最長公共後綴就是 $\mathrm{LCA}(x_1,\cdots,x_n)$。
3. 若某個狀態存在 $\mathrm{nxt}(c)$ 轉移,那麼其在 parent 樹上的祖先均存在 $\mathrm{nxt}(c)$ 轉移
子孫存在 $\mathrm{nxt}(c)$ 轉移,說明子孫出現的某個位置 $r_i\in \mathrm{endpos}(\text{子孫})$ 後面有一個字元 $c$。因為祖先是子孫的後綴,所以子孫出現的所有地方祖先均出現,那麼顯然有 $r_i\in \mathrm{endpos}(\text{祖先})$,則祖先也存在 $\mathrm{next}(c)$ 轉移。
4. 每個狀態的 $\mathrm{endpos}$ 集合為其在 parent 樹中子樹 $\mathrm{endpos}$ 集合的並集
我們在構建 SAM 的過程中,將 $last$ 所經過的狀態提取出來,則這些狀態分別包含子串 $s[1:i]$,$1\leq i\leq n$。那麼我們為 $s[1:i]$ 所在的狀態打上 $i$ 的標籤,表示 $i$ 為該狀態的一個出現位置。然後我們考慮該狀態在 parent 樹上的祖先們,由於祖先是子孫的後綴,那麼 $i$ 也是祖先們的一個出現位置,那麼我們可以將 $i$ 的標籤打在 $s[1:i]$ 所在狀態一直到 $state_0$ 的路徑上。對於所有 $s[1:i]$ 均這樣打標籤,最終每個狀態的 $\mathrm{endpos}$ 就是被打上的標籤集合。
不過這個結論暫時還不夠嚴謹,我們需要證明 $s[1:i]$ 所在狀態的子孫均不出現在位置 $i$。這也並不困難,因為一個子串出現在位置 $i$ 當且僅當其為 $s[1:i]$ 的一個後綴,而 $s[1:i]$ 的後綴僅會存在於 $s[1:i]$ 所在狀態到 $state_0$ 的路徑上,一定不在 $s[1:i]$ 所在狀態的子樹中。
淦,雖然感覺這裡有很多性質可以挖,但寫的時候只能列出比較顯然的幾條…另外的一些 DP 相關的性質需要在實際應用中體現吧。
補充5. 在 SAM 上,對於每個節點暴力跳後綴鏈接到 $state_0$,總的時間複雜度是 $\mathrm{O}(n^{1.5})$
雖然在少量部落格上看到這個性質,但是並沒有找到證明,不是十分確定。不過有題目用到了這個性質(如 2019 ICPC 徐州的 L 題),所以大概是對的。從直觀上確實比較難卡出很壞的情況。
1. 所有本質不同的子串及其出現次數(SAM 性質 / parent 樹上 DP)
由於 SAM 中所有狀態所表示的字元串都是互不相同的,所以本質不同的子串數量就是$\sum_{state}\mathrm{len}(state)-\mathrm{minlen}(state)+1$,即把每個狀態中包含的字元串數量全部加起來。


#include <map> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; const int C=26; //注意檢查字符集大小! ll ans=0; struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; //int nxt[N<<1][C]; map<int,int> nxt[N<<1]; //extend(char),並使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; //memcpy(nxt[clone],nxt[q],C*4); nxt[clone]=nxt[q]; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; ans+=len[cur]-len[link[cur]]; } }sam; int n; int a[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) sam.extend(a[i]),printf("%lld\n",ans); return 0; }
View Code
另一方面,某一子串的出現次數就等於其 $\mathrm{endpos}$ 集合的大小。根據性質「每個狀態的 $\mathrm{endpos}$ 集合為其在 parent 樹中子樹 $\mathrm{endpos}$ 集合的並集」,我們對於 $s[1:i]$ 所在狀態賦為 $1$,其餘狀態為 $0$,然後通過在 parent 樹上 dfs 求子樹中 $1$ 的個數即可。


#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=1000005; const int C=26; //注意檢查字符集大小! struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(char),並使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }sam; int n; char s[N]; int cnt[N<<1]; int main() { scanf("%s",s+1); n=strlen(s+1); for(int i=1;i<=n;i++) sam.extend(s[i]-'a'),cnt[sam.lst]=1; sam.sort(); ll ans=0; for(int i=sam.sz;i>=1;i--) { int id=sam.id[i]; if(cnt[id]>1) ans=max(ans,1LL*cnt[id]*sam.len[id]); cnt[sam.link[id]]+=cnt[id]; } printf("%lld\n",ans); return 0; }
View Code
在以上的實現中,並沒有顯式地對於 parent 樹進行 dfs,而是將所有狀態拓撲排序後按序處理。進行拓撲排序的策略並不複雜,我們只需要按照 $\mathrm{len}(state)$ 進行一趟桶排,這樣即可保證祖先($\mathrm{len}$ 較小)一定排在子孫($\mathrm{len}$ 較大)的前面,此時倒序即為一個合法的拓撲排序。
int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; }
2. 字典序第 K 大子串(SAM 上 DP)
我們先考慮本質相同的子串僅計算一次的情況。剛剛在計算本質不同子串數量的時候,我們利用狀態的性質解決了,但實際上還有一個在 SAM 上 DP 的做法。
有這樣的一個結論:一個字元串本質不同的子串數量,相當於在 SAM 上通過 $\mathrm{nxt}$ 轉移產生的路徑數量。我們嘗試理解這個結論。首先,這樣的計數一定不會少算(有子串沒被算到),因為每個本質不同的子串都會在 SAM 上存在唯一對應的路徑;同時,這個計數也不會多算(算到多餘的子串),因為 SAM 僅接受模式串的子串。
利用這個結論,我們直接利用 DP 計算從每個狀態出發的路徑數量即可(由於 $\mathrm{nxt}$ 轉移構成的圖是一個 DAG,我們仍然可以通過令 $\mathrm{len}$ 從小到大來獲得一個正拓撲序)。DP 的轉移方程為 $path[x]=1+\sum_{y=\mathrm{nxt}_x(c_i)}path[y]$,需要按照逆拓撲序依次計算。
對於本質相同的子串計算出現次數的情況,將上面轉移方程中的 $1$ 替換成 $cnt[x]$ 即可。
那麼求字典序第 $K$ 大子串,只需要從 $state_0$ 開始貪心,每次選取最小的前綴路徑數量大於等於 $K$ 的轉移即可(原理同線段樹上二分,只不過 SAM 上每個狀態有字符集大小的分叉)。


#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=500005; const int C=26; //注意檢查字符集大小! struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(char),並使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }sam; int n; char s[N]; int type,K; int cnt[N<<1]; ll path[N<<1][2]; int main() { scanf("%s",s+1); scanf("%d%d",&type,&K); n=strlen(s+1); for(int i=1;i<=n;i++) sam.extend(s[i]-'a'),cnt[sam.lst]=1; sam.sort(); for(int i=sam.sz;i>=0;i--) { int id=sam.id[i]; path[id][0]=1,path[id][1]=cnt[id]; for(int j=0;j<C;j++) { int nxt=sam.nxt[id][j]; if(nxt) for(int k=0;k<2;k++) path[id][k]+=path[nxt][k]; } if(id!=-1) cnt[sam.link[id]]+=cnt[id]; } if(path[0][type]-cnt[0]<K) printf("-1\n"); else { int cur=0; while(K) { for(int i=0;i<C;i++) { int nxt=sam.nxt[cur][i]; if(!nxt) continue; if(path[nxt][type]>=K) { cur=nxt,putchar('a'+i); K-=(type?cnt[cur]:1); break; } K-=path[nxt][type]; } } } return 0; }
View Code
3. 兩個字元串的最長公共子串(SAM 上匹配)
對於 $s,t$ 兩個字元串,對於 $s$ 串建立 SAM,$t$ 在這個 SAM 上進行匹配,失配時跳 $\mathrm{link}$。實現上和 AC 自動機差不多。
例題:SPOJ-LCS Longest Common Substring


#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=250005; const int C=26; //注意檢查字符集大小! struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(char),並使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }sam; int n,m; char s[N],t[N]; int main() { scanf("%s%s",s+1,t+1); n=strlen(s+1),m=strlen(t+1); for(int i=1;i<=n;i++) sam.extend(s[i]-'a'); int ans=0,cur=0,len=0; for(int i=1;i<=m;i++) { int p=cur; while(p!=-1 && !sam.nxt[p][t[i]-'a']) p=sam.link[p],len=sam.len[p]; if(p!=-1) cur=sam.nxt[p][t[i]-'a'],len++; else cur=len=0; ans=max(ans,len); } printf("%d\n",ans); return 0; }
View Code
4. 多個字元串的最長公共子串(SAM 上匹配 + parent 樹上 DP)
想同時處理所有字元串是比較困難的,我們考慮先對於一個串建立 SAM,然後對於其餘的串依次求出「當匹配到狀態 $state$ 時,最長的匹配長度」。
考慮對於具體某一個待匹配串 $t$,我們還是像兩個字元串一樣求 $t[1:i]$ 在 SAM 上匹配得到的狀態以及匹配上的長度 $len$。但不同的是,我們還需要額外維護一個數組 $curlen$,表示字元串 $t$ 對於每個狀態的 $\mathrm{longest}(state)$ 能匹配的最長後綴長度。更新的規則為 $curlen[x]=\mathrm{max}(curlen[x],len)$,因為 $t[1:i]$ 所對應的狀態可能由多個狀態轉移而來,我們需要取其中最大的匹配長度。
需要注意到,我們在維護 $curlen$ 的過程中,只考慮到了 $t[1:i]$ 這不超過 $|t|$ 個狀態,但實際上對於 SAM 上的任意狀態均應計算 $curlen$。所以我們按照 $\mathrm{len}$ 從大到小的順序計算沒經過的狀態的 $curlen$,並使用 $curlen[x]$ 來更新 $curlen[\mathrm{link}(x)]$,規則為 $curlen[\mathrm{link}(x)]=\mathrm{max}(curlen[\mathrm{link}(x)],curlen[x])$。
對於一個待匹配串 $t$ 我們能按照如上的方法求得每個狀態的 $curlen$,那麼所有字元串的在每個狀態的最長匹配長度,就是 $ans[state]=\mathrm{min}_t(curlen_t[state])$。而最終答案為 $\mathrm{min}_{state}(ans[state])$。
例題:SPOJ-LCS2 Longest Common Substring II


#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; const int C=26; //注意檢查字符集大小! struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }sam; int n,m; char s[N],t[N]; int ans[N<<1],curlen[N<<1]; int main() { scanf("%s",s+1); n=strlen(s+1); for(int i=1;i<=n;i++) sam.extend(s[i]-'a'); sam.sort(); for(int i=1;i<=sam.sz;i++) ans[i]=sam.len[i]; while(~scanf("%s",t+1)) { m=strlen(t+1); int cur=0,len=0; for(int i=1;i<=m;i++) { int p=cur,c=t[i]-'a'; while(p!=-1 && !sam.nxt[p][c]) p=sam.link[p],len=sam.len[p]; if(p!=-1) cur=sam.nxt[p][c],len++; else cur=len=0; //對於同一cur,可能從多個p轉移過來,故不能用len直接賦值cur curlen[pos]=max(curlen[pos],len); } for(int i=sam.sz;i>=1;i--) { int id=sam.id[i]; curlen[sam.link[id]]=max(curlen[sam.link[id]],curlen[id]); } for(int i=1;i<=sam.sz;i++) ans[i]=min(ans[i],curlen[i]),curlen[i]=0; } int fans=0; for(int i=1;i<=sam.sz;i++) fans=max(fans,ans[i]); printf("%d\n",fans); return 0; }
View Code
在上文中處理多個字元串的問題時,我們先對於其中一個字元串建立 SAM,對於剩餘的字元串依次在這個 SAM 上面跑。有沒有辦法對於多個字元串直接建立一個自動機,使得任意字元串的任意子串都能被自動機接受?答案是肯定的。
我們考慮這樣的實現:對於字元串 $s_1,\cdots,s_n$,我們首先對於 $s_1$ 使用 $extend()$ 函數依次插入建立 SAM,接著我們將 $last$ 移回 $state_0$ 並重新依次插入 $s_2$。這個實現的邏輯比較簡單,對於能夠「接受任意字元串的任意子串」的正確性也是比較顯然的,不過在細節上存在一些問題:對於多次經過同一個狀態時反覆插入會產生孤立聯通塊,這些孤立連通塊內的點在進行從 $state_0$ 開始的匹配時永遠不會被走到(詳見 ix35 – 悲慘故事 長文警告 關於廣義 SAM 的討論)。這種現象的存在會導致進行拓撲排序等操作時出錯(一個例子為 yy1695651 – ICPC2019 G題廣義SAM的基排為什麼不行?)。
另一方面,上述方法的複雜度與 $\sum_i |s_i|$ 線性相關,因為相當於依次插入 $n$ 個字元串。但假如題目中的字元串不是直接給出的,而是採用 trie 樹的形式,那麼 $n$ 個節點的 trie 樹可以產生總長為 $n^2$ 級別的字元串,其形狀大概如下:
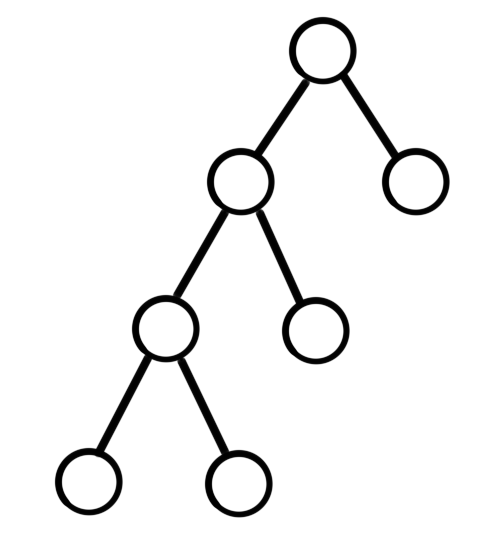
出於適用範圍更廣的原則,本文介紹基於 trie 樹和離線 bfs 的廣義 SAM 實現方法。其能夠建立正確的廣義 SAM,同時時空複雜度僅與 trie 樹的節點數相關。
我們從 trie 樹的角度來考慮 SAM 的實現。由於模式串僅為單一字元串,所以對於 SAM 而言是基於退化為一條鏈的 trie 樹建立的。
那麼對於一個非退化的 trie 樹,我們也可以在修改很少幾處的情況下建立 GSA。
1. 插入順序
在建立 SAM 的過程中,我們是按照字元串中從前到後的順序依次擴展 SAM 的,從 trie 樹的角度看就是從淺到深。那麼在建立 GSA 時,我們為了保證先擴展較淺的節點、再擴展較深的節點,可以採用 bfs 進行實現。
如果不採用從淺到深的順序,就可能出現由狀態 $x$ 轉移到狀態 $y$、而狀態 $y$ 已經先求完 $\mathrm{nxt}$ 與 $\mathrm{link}$ 的情況,此時會產生類似每次重置 $last$ 一樣的孤立連通塊問題,需要額外的不少討論才能保證正確性。使用從淺到深的 bfs 則不會出現這種情況。
2. 節點標號
在建立 GSA 前,我們首先需要用 $\mathrm{nxt}$ 數組來建立 trie 樹。因此每步插入的 $cur$ 都是已經建好的節點,無須開新點;只有 $clone$ 需要動態開點。同時,由於我們按照深度擴展,每次的 $last$ 都是通過 bfs 得知的,無須再額外維護 $last$ 這個變數。
3. 資訊隔離
在建立 SAM 的過程中,我們在插入 $s[i]$ 時不會知道任何 $s[j]$($j>i$)的資訊。但是在建立 GSA 時,我們有可能獲得更深節點的資訊,具體來說就是 $\mathrm{nxt}_{last}$ 可能指向比 $last$ 更深的節點。因此我們需要仔細檢查之前 SAM 的板子中所有用到 $\mathrm{nxt}$ 的地方:
void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; //nxt[lst][c]一定存在,且等於cur【會產生問題 #1】 while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; //這裡我們認為dep[p]<dep[lst], //那麼假如nxt[p][c]是某次clone賦值的,說明那次clone在當前擴展操作之前,那麼直接使用是ok的; //假如nxt[p][c]是構建trie樹時賦值的,則dep[q]=dep[p]+1<=dep[lst]<dep[cur],說明一定已經被擴展到了。 //綜上,【不會產生問題】 if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); //假如nxt[q][i]是構建trie樹時賦值的,dep[nxt[q][i]]最大可以等於dep[cur], //即使nxt[q][i]與cur同深度,在廣義SAM的擴展過程中也有先後之分, //所以如果擴展cur時未擴展過nxt[q][i],那麼nxt[q][i]在此時應該視為0【會產生問題 #2】 while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; //同q=nxt[p][c]處的分析,對於nxt[p][c]的使用都是安全的【不會產生問題】 link[q]=link[cur]=clone; } } lst=cur; }
我們需要對於會產生問題的兩處稍加修改,具體而言:
(1) 在 #1 處,初始令 $p=\mathrm{link}[lst]$ 即可(因為 $\mathrm{nxt}[lst][c]=cur$ 在構建 trie 樹時就被賦值了;而其餘所有 $\mathrm{nxt}[p][c]$ 假如為非 clone 點,在 trie 樹上的深度一定小於 $dep[cur]$,則可以直接使用 );
(2) 在 #2 處,我們對於 $q$ 的每一個 $\mathrm{nxt}$ 轉移,均檢查是否被擴展過(等價於檢查 $\mathrm{len}$ 是否為 $0$),若未被擴展過,即使 $\mathrm{nxt}[q][i]\neq 0$ 也必須視為 $0$。
綜合以上三點,我們可以寫出如下的 GSA 的實現:
typedef pair<int,int> pii; const int N=1000005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct GeneralSuffixAutomaton { int sz; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(int,char) GeneralSuffixAutomaton() { len[0]=0,link[0]=-1; sz=0; } //向trie樹上插入一個字元串 void insert(char *s,int n) { for(int i=1,cur=0;i<=n;i++) { int c=s[i]-'a'; if(!nxt[cur][c]) nxt[cur][c]=++sz; cur=nxt[cur][c]; } } //擴展GSA,對於lst的c轉移進行擴展 int extend(int lst,int c) { int cur=nxt[lst][c]; len[cur]=len[lst]+1; int p=link[lst]; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; for(int i=0;i<C;i++) nxt[clone][i]=len[nxt[q][i]]?nxt[q][i]:0; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } return cur; } //基於trie樹建立GSA void build() { queue<pii> Q; for(int i=0;i<C;i++) if(nxt[0][i]) Q.push(pii(0,i)); while(!Q.empty()) { pii tmp=Q.front(); Q.pop(); int cur=extend(tmp.first,tmp.second); for(int i=0;i<C;i++) if(nxt[cur][i]) Q.push(pii(cur,i)); } } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }gsa;
1. 本質不同的子串數量及出現次數
本質不同的子串數量還是利用 GSA 的性質即可,等於 $\sum_{state}\mathrm{len}(state)-\mathrm{len}\left(\mathrm{link}(state)\right)$。
例題:洛谷P6139 【模板】廣義後綴自動機(廣義 SAM)


#include <queue> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=1000005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct GeneralSuffixAutomaton { int sz; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(int,char) GeneralSuffixAutomaton() { len[0]=0,link[0]=-1; sz=0; } //向trie樹上插入一個字元串 void insert(char *s,int n) { for(int i=1,cur=0;i<=n;i++) { int c=s[i]-'a'; if(!nxt[cur][c]) nxt[cur][c]=++sz; cur=nxt[cur][c]; } } //擴展GSA,對於lst的c轉移進行擴展 int extend(int lst,int c) { int cur=nxt[lst][c]; len[cur]=len[lst]+1; int p=link[lst]; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; for(int i=0;i<C;i++) nxt[clone][i]=len[nxt[q][i]]?nxt[q][i]:0; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } return cur; } //基於trie樹建立GSA void build() { queue<pii> Q; for(int i=0;i<C;i++) if(nxt[0][i]) Q.push(pii(0,i)); while(!Q.empty()) { pii tmp=Q.front(); Q.pop(); int cur=extend(tmp.first,tmp.second); for(int i=0;i<C;i++) if(nxt[cur][i]) Q.push(pii(cur,i)); } } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }gsa; int n,m; char s[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%s",s+1); m=strlen(s+1); gsa.insert(s,m); } gsa.build(); ll ans=0; for(int i=1;i<=gsa.sz;i++) ans+=gsa.len[i]-gsa.len[gsa.link[i]]; printf("%lld\n",ans); return 0; }
View Code
出現次數也是在 parent 樹上 DP。
這道題中,具體一個狀態產生的貢獻是 $\left(\mathrm{len}(state)-\mathrm{minlen}(state)+1\right)\cdot cnt_1[state]\cdot cnt_2[state]$。


#include <queue> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=400005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct GeneralSuffixAutomaton { int sz; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(int,char) GeneralSuffixAutomaton() { len[0]=0,link[0]=-1; sz=0; } //向trie樹上插入一個字元串 void insert(char *s,int n) { for(int i=1,cur=0;i<=n;i++) { int c=s[i]-'a'; if(!nxt[cur][c]) nxt[cur][c]=++sz; cur=nxt[cur][c]; } } //擴展GSA,對於lst的c轉移進行擴展 int extend(int lst,int c) { int cur=nxt[lst][c]; len[cur]=len[lst]+1; int p=link[lst]; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; for(int i=0;i<C;i++) nxt[clone][i]=len[nxt[q][i]]?nxt[q][i]:0; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } return cur; } //基於trie樹建立GSA void build() { queue<pii> Q; for(int i=0;i<C;i++) if(nxt[0][i]) Q.push(pii(0,i)); while(!Q.empty()) { pii tmp=Q.front(); Q.pop(); int cur=extend(tmp.first,tmp.second); for(int i=0;i<C;i++) if(nxt[cur][i]) Q.push(pii(cur,i)); } } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }gsa; int n,m; char s[N],t[N]; int cnt1[N<<1],cnt2[N<<1]; int main() { scanf("%s",s+1); n=strlen(s+1); scanf("%s",t+1); m=strlen(t+1); gsa.insert(s,n); gsa.insert(t,m); gsa.build(); gsa.sort(); for(int i=1,cur=0;i<=n;i++) { cur=gsa.nxt[cur][s[i]-'a']; cnt1[cur]++; } for(int i=1,cur=0;i<=m;i++) { cur=gsa.nxt[cur][t[i]-'a']; cnt2[cur]++; } ll ans=0; for(int i=gsa.sz;i>=1;i--) { int id=gsa.id[i]; int lst=gsa.link[id]; ans+=1LL*(gsa.len[id]-gsa.len[lst])*cnt1[id]*cnt2[id]; cnt1[lst]+=cnt1[id]; cnt2[lst]+=cnt2[id]; } printf("%lld\n",ans); return 0; }
View Code
多個字元串的最長公共子串也許不能用 GSA 做
SPOJ 的那題是比較弱的,因為 $n\leq 10$,所以可以存個長度為 $10$ 的數組搞一搞。以下討論的是 $n, \sum_i |s_i|\leq 1\times 10^6$ 級別的該問題。
在 SAM 上,疑似對於每個狀態暴力跳 fail 是 $\mathrm{O}(n^{1.5})$ 的。那麼在 GSA 上,是否能夠保證所有串各自佔有的狀態之和是 $|s_i|^{1.5}$ 呢?這個結論是存疑的…就算成立,時間複雜度也明顯比 SAM 要差。
SAM / GSA 的裸題一般都是一眼會,稍微難一點的題目會在此基礎上套線段樹合併、LCT access 維護樹鏈等內容,但此時難點就不再 SAM 上了。做到啥補充啥吧。
Kattis-firstofhername First of Her Name(2019 ICPC WF)【GSA 裸題】
題目中給定了一棵 trie 樹,所以建立 GSA 是比較自然的想法。考慮回答查詢,某個字元串的前綴如果是 $s$,就相當於反轉的 $s$ 是從 trie 樹的對應位置到 $state_0$ 的路徑的前綴。所以我們只需要用類似求出現次數的方法,對於每個字元串在結尾處令 $cnt=1$(在這題中就是將 $cnt[1:n]$ 均置 $1$),然後按照拓撲序 DP 即可。


#include <queue> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=1000005; const int C=26; //注意檢查字符集大小! ll cnt[N<<1]; //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct GeneralSuffixAutomaton { int sz; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(int,char) GeneralSuffixAutomaton() { len[0]=0,link[0]=-1; sz=0; } //擴展GSA,對於lst的c轉移進行擴展 int extend(int lst,int c) { int cur=nxt[lst][c]; len[cur]=len[lst]+1; int p=link[lst]; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; for(int i=0;i<C;i++) nxt[clone][i]=len[nxt[q][i]]?nxt[q][i]:0; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } return cur; } //基於trie樹建立GSA void build() { queue<pii> Q; for(int i=0;i<C;i++) if(nxt[0][i]) Q.push(pii(0,i)); while(!Q.empty()) { pii tmp=Q.front(); Q.pop(); int cur=extend(tmp.first,tmp.second); for(int i=0;i<C;i++) if(nxt[cur][i]) Q.push(pii(cur,i)); } } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }gsa; int n,q; char s[N]; int main() { scanf("%d%d",&n,&q); for(int i=1;i<=n;i++) { char ch=getchar(); while(ch<'A' || ch>'Z') ch=getchar(); int lst; scanf("%d",&lst); gsa.nxt[lst][ch-'A']=i,cnt[i]=1; } gsa.sz=n; gsa.build(); gsa.sort(); for(int i=gsa.sz;i>=1;i--) { int id=gsa.id[i]; cnt[gsa.link[id]]+=cnt[id]; } while(q--) { scanf("%s",s+1); int n=strlen(s+1); int cur=0; for(int i=n;i>=1;i--) { int c=s[i]-'A'; if(!gsa.nxt[cur][c]) { cur=0; break; } cur=gsa.nxt[cur][c]; } printf("%d\n",gsa.len[cur]>=n?cnt[cur]:0); } return 0; }
View Code
計蒜客42551 Loli, Yen-Jen, and a cool problem(2019 ICPC 徐州)【GSA 基礎性質,去重處理】
這題本身挺裸的。對於每次詢問 $s[x-L+1:x]$ 的出現次數,我們只需要找到其所在的狀態就行了,從 $x$ 沿著 $\mathrm{link}$ 暴力跳、直到當前狀態的 $\mathrm{len}$ 區間包含 $L$ 即可。理論上需要將 $x$ 相同的詢問同時處理,不過數據貌似沒卡。
這題稍微有點噁心的是 trie 樹上會有重合的節點。對於重合的節點,我們選擇最早出現的一個作為代表,其餘節點全部映射到代表。這會導致非代表點變成孤立連通塊,在進行拓撲排序的時候需要注意忽略這些 $\mathrm{len}=0$ 的孤立點。


#include <queue> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=300005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct GeneralSuffixAutomaton { int sz; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(int,char) GeneralSuffixAutomaton() { len[0]=0,link[0]=-1; sz=0; } //擴展GSA,對於lst的c轉移進行擴展 int extend(int lst,int c) { int cur=nxt[lst][c]; len[cur]=len[lst]+1; int p=link[lst]; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; for(int i=0;i<C;i++) nxt[clone][i]=len[nxt[q][i]]?nxt[q][i]:0; while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } return cur; } //基於trie樹建立GSA void build() { queue<pii> Q; for(int i=0;i<C;i++) if(nxt[0][i]) Q.push(pii(0,i)); while(!Q.empty()) { pii tmp=Q.front(); Q.pop(); int cur=extend(tmp.first,tmp.second); for(int i=0;i<C;i++) if(nxt[cur][i]) Q.push(pii(cur,i)); } } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) if(len[i]) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) if(len[i]) id[bucket[len[i]]--]=i; } }gsa; int n,q; char s[N]; int to[N]; ll cnt[N<<1]; int main() { scanf("%d%d",&n,&q); scanf("%s",s+1); gsa.nxt[0][s[1]-'A']=1,to[1]=1,cnt[1]++; for(int i=2;i<=n;i++) { int x,c=s[i]-'A'; scanf("%d",&x); x=to[x]; if(!gsa.nxt[x][c]) gsa.nxt[x][c]=i; to[i]=gsa.nxt[x][c]; cnt[to[i]]++; } gsa.sz=n; gsa.build(); gsa.sort(); for(int i=gsa.sz;i>=1;i--) { int id=gsa.id[i]; if(id) cnt[gsa.link[id]]+=cnt[id]; } while(q--) { int x,y; scanf("%d%d",&x,&y); x=to[x]; while(gsa.len[gsa.link[x]]>=y) x=gsa.link[x]; printf("%lld\n",cnt[x]); } return 0; }
View Code
牛客4010D 卡拉巴什的字元串(2020 Wannafly Camp Day2)【題意轉化,SAM 基礎性質】
我們考慮依次加入字元,那麼在加到 $s[i]$ 時,我們需要考慮 $s[1:i-1]$ 的答案與 $s[1:i]$ 的區別。假如加入 $s[i]$ 會使得答案發生改變,那麼最長的 LCP 一定是一個 $s[1:i]$ 的後綴,否則該 LCP 也一定在 $s[1:i-1]$ 中出現過了。
通過這樣的轉化後,我們只需要關心最長的、出現過多次的 $s[1:i]$ 的後綴是什麼。在插入完 $s[i]$ 後,SAM 的 $last$ 指針指向 $\mathrm{endpos}=\{i\}$ 的狀態,那麼根據後綴鏈接的性質,$\mathrm{link}(last)$ 恰為我們所要的東西(因為其 endpos 集合大於 $1$,即出現多次),所以答案即為 $\mathrm{len}(\mathrm{link}(last))$ 的 MEX。有一個細節是,當字元串為形如 “aaaa” 時答案應該全是 $0$,因為 LCP 的值為 $-,1,2,3$,並沒有出現過 $0$。


#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=1000005; const int C=26; //注意檢查字符集大小! //在結構題外開任何與SAM狀態相關的數組,都需要N<<1 struct SuffixAutomaton { int sz,lst; //狀態數上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(char),並使用nxt[clone]=nxt[q]替換memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void init() { for(int i=0;i<=sz;i++) { len[i]=link[i]=0; for(int j=0;j<C;j++) nxt[i][j]=0; } link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } int id[N<<1]; //構建完成後,id順序為len遞增(逆拓撲序)【僅可排一次】 void sort() { static int bucket[N<<1]; memset(bucket,0,sizeof(bucket)); for(int i=1;i<=sz;i++) bucket[len[i]]++; for(int i=1;i<=sz;i++) bucket[i]+=bucket[i-1]; for(int i=1;i<=sz;i++) id[bucket[len[i]]--]=i; } }sam; int n; char s[N]; int main() { int T; scanf("%d",&T); while(T--) { scanf("%s",s+1); n=strlen(s+1); sam.init(); printf("0"); sam.extend(s[1]-'a'); int mx=0,zero=0; for(int i=2;i<=n;i++) { sam.extend(s[i]-'a'); int val=sam.len[sam.link[sam.lst]]; mx=max(mx,val); zero|=(val==0); printf(" %d",zero?mx+1:0); } printf(" \n"); } return 0; }
View Code
牛客38727C Cmostp(2022 牛客暑期多校 加賽)【LCT access 維護 parent 樹的鏈並,離線轉化】
這題其實只有模型抽象用到了 SAM,所以題解寫在 LCT 那裡了。右端點在區間 $[l,r]$ 的狀態等價於字元串 $s[1:l]$ 到 $s[1:r]$ 這 $r-l+1$ 個狀態在 parent 樹上的鏈並。
(待續)
SAM 在處理字典序相關問題時比較乏力,在這種情況下從後綴樹、後綴數組的角度往往具有更好的性質。
當問題中的詢問數是 $|s|$ 級別的時,可以往 SAM 想一想。
