序列標註（HMM/CRF）

• 2019 年 10 月 4 日
• 筆記

簡介

序列標註（Sequence Tagging）是一個比較簡單的NLP任務，但也可以稱作是最基礎的任務。序列標註的涵蓋範圍是非常廣泛的，可用於解決一系列對字元進行分類的問題，如分詞、詞性標註、命名實體識別、關係抽取等等。

對於分詞相信看過之前部落格的朋友都不陌生了，實際上網上已經有很多開源的中文分詞工具，jieba、pkuseg、pyhanlp…這裡都不一一列舉了，我們也不再作過多的討論。接下來都是以實體識別作為示例來講解，而其他任務的實現都是基本一致，只是標註方式的不同罷了。

對於實體識別任務，我們有一段待標註的序列(X = {x_1, x_2,…,x_n})，我們需要對該序列的每一個(x_i)預測一個對應的Tag，在通常情況下，我們對tag進行如下定義：

• B – Begin，表示開始
• I – Intermediate，為中間字
• E – End，表示結尾
• S – Single，表示單個字元
• O – Other，表示其他，用於標記無關字元

常見標籤方案通常為三標籤或者五標籤法：

• IOB – 對於文本塊的第一個字元用B標註，文本塊的其它字元用I標註，非文本塊字元用O標註
• IOBES – 對於文本塊的第一個字元用B標註，文本塊的最後一個字元用E標註，文本塊的其它字元用I標註，非文本塊用O標註

當然這樣的tag並不是固定的，根據任務不同還可以對標籤有一系列靈活的變化或擴展。對於分詞任務，我們可以用同樣的標註方式來標註每一個詞的開頭、結尾，或單字。如詞性標註中，我們可以將標籤定義為：n、v、adj…而對於更細類別的命名實體識別任務，我們在定義的標籤之後加上一些後綴，如：B-Person、B-Location…這都可以根據你的實際任務來自行選擇。

處理序列標註問題的常用模型包括隱馬爾可夫模型（HMM）、條件隨機場（CRF）、BiLSTM + CRF，由於篇幅的限制，這一節先介紹兩個傳統的機器學習模型：隱馬爾可夫模型和條件隨機場

隱馬爾可夫模型（HMM）

HMM屬於經典的機器學習演算法，屬於有向圖模型的一種，主要用於時序數據建模。隨著深度學習的發展，HMM在序列標註上用的比較少了，但也是做序列標註的一種基本思路。原理比較簡單，已經掌握的同學可以跳過這一段，下面也只進行簡單的介紹，想要詳細了解的同學可以看看周志華老師的西瓜書，講的非常詳細的了。

HMM模型中的變數可以分為兩組：

• 觀測變數： (X = {x_1, x_2,…,x_n})，用於表示第(i)個時刻的觀測值
• 狀態變數： (Y = {y_1, y_2,…,y_n})，用於表示第(i)個時刻的隱藏狀態，通常該狀態是隱藏的，因此也稱其為隱變數。
• 狀態空間：(S = {s_1, s_2, …,s_N})，用於表示狀態變數通常的取值範圍。

顯然，在序列標註任務中，待標註序列就對應觀測變數，標註結果對應狀態變數，而我們定義的標籤類別就對應狀態空間。對應的隱馬爾可夫模型結構如下圖所示：

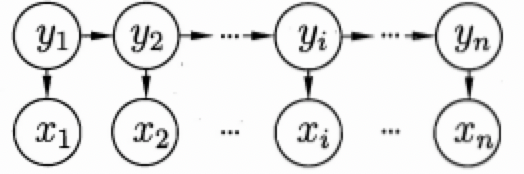
上圖的箭頭表示變數間的依賴關係，即一種馬爾可夫鏈結構，整個模型基於下面的隱馬爾可夫假設：

• 在任一時刻，觀測變數的取值僅僅依賴於狀態變數，即(x_t)由(y_t)決定，與其他時刻的狀態變數及觀測變數無關（這就類似於一個unigram模型）, 即
  [P(x_t|X, Y) = P(x_t|y_t)]
• 在任一時刻，系統下一時刻的狀態僅由當前狀態決定，不依賴以往的任何狀態，(y_t)僅與(y_{t-1})有關，與其他都無關。這個假設意味著我們的隱變數是包含時序資訊的，這是簡單的分類模型所不具備的。即
  [P(y_t|X, Y) = P(y_t|y_{t-1})]

根據上述假設，則我們就可以對所有變數的聯合概率分布進行建模：
[P(x_1, y_1, …, x_n, y_n)=P(y_1)P(x_1|y_1)prod^n_{i=2}P(y_i|y_{i-1})P(x_i|y_i)]

有了上述表達式，如果我們能夠學習得到各個狀態的初始概率(P(y_1))，各個狀態之間的轉移概率(P(y_i|y_{i-1}))，以及觀測概率(P(x_i|y_i))，我們即可對任意序列計算得到我們的聯合概率分布，從而選擇最大概率的狀態變數作為我們的預測結果。因此，HMM的主要有如下三組參數：

• 狀態轉移概率（Transition probabilities）：模型在各個狀態之間轉換的概率，通常記為矩陣(A=[a_{i, j}]_{N times N})，其中
  [a_{i, j} = P(y_{t+1}=s_j|y_t=s_i), sum_{i=1}^Na_{i, j}=1,1 le i,j le N]
  • 其表示在任意時刻(t)，若狀態為(s_i)，則下一時刻狀態為(s_j)的概率
• 輸出觀測概率（Emission probabilities）：模型根據當前狀態獲得各個觀測值的概率，通常記為矩陣(B=[b_{i, j}]_{N times M})，其中
  [b_{i, j} = P(x_{t}=o_j|y_t=s_i), sum_{i=1}^Nb_{i, j}=1, 1 le i le N, 1 le j le M]
  • 其表示任意時刻(t)，若狀態為(s_i)，則觀測值(o_j)被獲取的概率
• 初始狀態概率（Start probabilities）：模型在初始時刻各個狀態出現的概率，通常記為(pi = [pi_1, pi_2, …, pi_N])，其中
  [pi_i = P(y_1=s_i), sum_{i=1}^Npi_i=1, 1 le i le N]

通常將其記為(lambda=[A, B, pi])則聯合概率分布即可化為如下表達式：
[P(X, Y|lambda) = pi_{y_1}b_{y_1, x_1}prod^n_{i=2}a_{y_{i-1}, y_i}b_{y_i, x_i}]

概率圖模型均存在三個基本問題，這也是我們求解概率圖模型的基本步驟：

• 評估問題（Evaluation Problem）：給定(lambda)和觀測變數(X)，如何計算一個觀測變數的概率(P(X|lambda))，用於評估模型與實際問題的匹配程度（前向後向演算法）
• 學習問題（Learning Problem）：給定若干觀測序列(X)，如何學習參數(lambda=[A, B, pi])，使得計算出的(P(X|lambda))最大化（有監督下的極大似然估計）
• 解碼問題（Decoding Problem）：給定(lambda)和觀測變數(X)，如何求出最可能的隱藏序列(P(Y|X, lambda))（維特比演算法）

條件隨機場（CRF）

HMM屬於生成式模型，直接對聯合分布(P(X, Y))進行建模。CRF在某些方面與HMM有些類似，但屬於一種判別式無向圖模型，其對條件分布進行建模。具體來說，對於觀測序列(X)和標記序列(Y)，CRF的目標就是構建條件概率模型(P(Y|X))。

馬爾可夫隨機場

馬爾可夫隨機場又稱為概率無向圖模型，其表示一個聯合概率分布。對於一個無向圖模型(G=[V, E])，(V)表示該無向圖中的所有節點，(E)表示無向圖中的所有無向邊。如果無向圖中各個節點之間的聯合概率分布滿足馬爾可夫性，則稱此聯合概率分布為馬爾可夫隨機場或概率無向圖模型。

馬爾可夫性：任意節點對所有節點的條件概率分布等於其對其相鄰節點的條件概率分布
[P(y_v|Y_{V/{v}})=P(y_v|Y_{n(v)})]

其中(Y_{V/{v}})表示無向圖中除(y_v)意外的所有節點，(Y_{n(v)})表示與(y_v)相鄰的所有節點。簡單概括馬爾可夫性就是不相鄰節點之間條件獨立，或每一個節點僅由相鄰節點所決定。作為一個無向圖模型，其沒有HMM模型那樣嚴格的假設

條件隨機場

條件隨機場為一種特殊的馬爾可夫隨機場，表示的是給定一組輸入，得到的輸出滿足馬爾可夫隨機場。

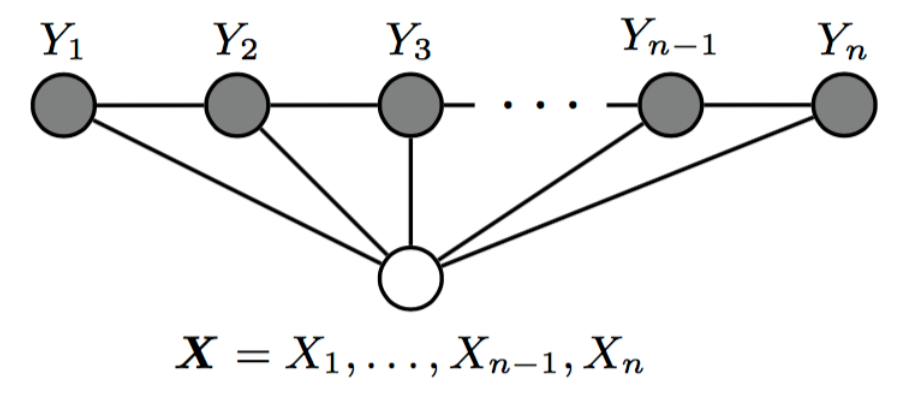
對於我們的序列標註任務，我們所說的CRF通常都指鏈式CRF，如上圖所示，即每個無向圖模型為一個線性鏈模型，每一個節點僅與兩個節點相鄰，則每一個節點對所有節點的條件概率分布滿足：
[P(y_t|X, Y_{V/{v}}) = P(y_t|X, y_{t-1}, y_{t+1})]

其中當(t)取(1)或(n)時只考慮單邊。

條件隨機場的特徵函數

CRF對於條件概率(P(Y|X))的建模是比較複雜的，但仔細看完下面的講解你很快就能完全掌握了。條件隨機場中的參數化形式的條件概率定義如下所示：
[P(y|x)=frac{1}{Z}exp(sum_jsum_{i=1}^{n-1}lambda_it_j(y_{i+1}, y_i, x, i)+ sum_ksum_{i=1}^{n}mu_ks_k(y_i, x, i))]

其中：

• (t_j(y_{i-1}, y_i, x, i))為局部特徵函數，該特徵由當前節點和上一個節點決定，稱其為狀態轉移特徵，用以描述相鄰節點以及觀測變數對當前狀態的影響；
• (s_k(y_i, x, i))為節點特徵函數，該特徵函數只和當前節點有關，稱其為狀態特徵；
• (lambda)和(mu)是對應特徵函數的參數。

在序列標註任務中，通常情況下，我們將其表示為條件隨機場的矩陣形式，這更便於我們理解與計算：

對於鏈式條件隨機場，我們首先定義兩個特殊節點：(y_0=<START>)，(y_{n+1}=<STOP>)。
對觀測序列(X)的每一個位置(i = 1, 2, …, n+1)，定義一個N階矩陣（N是隱藏狀態的個數），這個矩陣等效于于HMM模型中的狀態轉移矩陣：
[M_i(x)=[M_i(y_{i-1}, y_i|x)]]

[M_i(y_{i-1}, y_i|x)=exp(W_i(y_{i-1}, y_i|x))]

[W_i(y_{i-1}, y_i|x)=sum_{k=1}^{K} w_kf_k(y_{i-1}, y_i, x, i)]

其中(f_k(y_{i-1}, y_i, x, i))是將狀態轉移特徵(t_j(y_{i-1}, y_i, x, i))以及狀態特徵(s_k(y_i, x, i))統一化的符號表示，(w_k)為對應特徵參數的統一化符號表徵（詳細的表徵方法可以參考李航老師的《統計學習方法》的197頁），這樣，我們就得到了一個類似於HMM的狀態轉移矩陣，轉移概率可以通過該序列n+1個矩陣適當元素的乘積表示，即(prod_{i=1}^{n+1}M_i(y_{i-1}, y_i|x))。但需要注意，這個狀態轉移矩陣(M)是非規範化的（所有概率累加不為1），我們可以歸一化最後的條件概率為：
[P_w(Y|X) = frac{1}{Z_w(x)}prod_{i=1}^{n+1}M_i(y_{i-1}, y_i|x)]

其中：(Z_w(x)=(M_1(x)M_2(x)…M_{n+1})_{start,stop})表示從開始狀態到終止狀態所有路徑上的非規範化概率只和，即一個規範化因子，將非規範化概率規範化。

HMM的轉移概率是受到約束的，而CRF的轉移矩陣可以是任一權重，只需最後進行全局歸一化就行了，這使得CRF較HMM顯得更加靈活

CRF與HMM的對比

CRF較HMM更為強大，主要由如下幾個原因：

• 每一個HMM都可以等效為一個特殊的CRF；
• CRF的隱藏狀態可以依賴更廣泛的資訊（前後相鄰的隱藏狀態以及所有的觀測變數），而HMM只能依賴上一個時刻的隱藏狀態以及當前時刻的觀測資訊；
• CRF參數矩陣的取值沒有限制（為非歸一化概率），而HMM的參數取值需要受到限制。

維特比演算法（Viterbi）

維特比演算法用動態規劃方法求解最短路徑問題，可以用於HMM模型以及CRF模型的解碼。

維特比演算法需要如下三個元素：

• 初始狀態概率(pi)
• 狀態轉移概率
• 輸出觀測概率

由之前的介紹我們已經了解，這三個概率在HMM模型和CRF模型都為可求的。

演算法基於這樣一個思想：最優路徑的子路徑也一定是最優的。
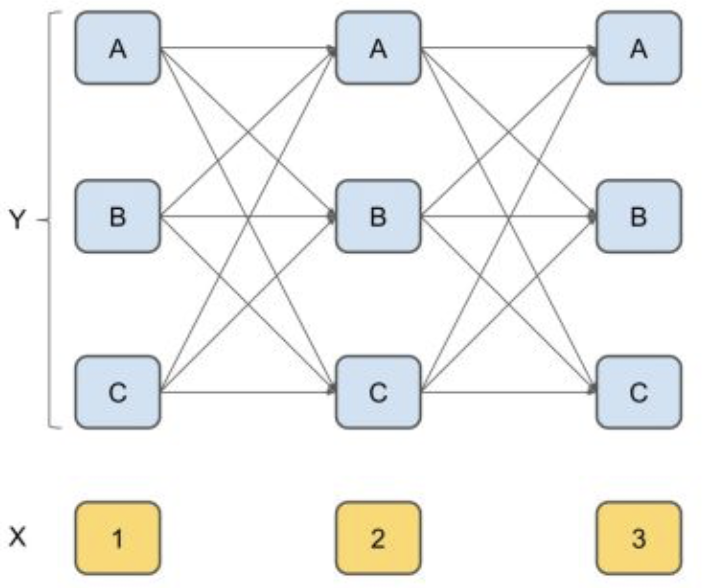
舉一個栗子就可以很清楚的明白了，假設我們有一個句子：「我愛北京天安門」。如果我們採用BIO的標註方法進行標註，則每個字的有3種可能的隱藏狀態。我們按照以下的方法來求解每一層的條件概率：

• 求第一個字任一節點(p_{1j})（每個節點對應一個隱藏狀態）的初始狀態概率，保存在該節點；
• 對第二個字的任一節點(p_{2j})，利用第一層的每一個節點的概率以及對應的狀態轉移概率，計算出到每個上一層節點到(p_{2j})的概率，並選擇最大的概率及其對應的上一個節點保存在該節點，則我們記錄了到達第二層每一個節點的最大概率以及對應的上一步位置。
• 對於第三個字的任一節點(p_{3j})，利用第二層保存的最大概率及其轉移概率，同樣計算出每個上層節點到(p_{3j})的概率，並選擇最大的概率及其對應的上一個節點保存在該節點，則我們記錄了到達第三層每一個節點的最大概率及上一步位置。
• 同理，後面每一層都利用上一層已有的最大概率及其轉移概率，計算出當前層每一個最大的狀態概率，並同時保存上一步的位置，直到最後一層。
• 到了最後一層，我們可以得到三個狀態中概率最高的一個節點，別忘了，我們在存儲最大概率的同時，還存儲了上一個字的狀態，這樣，我們可以反向得到所有字對應的隱藏狀態啦。

參考鏈接
https://blog.csdn.net/shuibuzhaodeshiren/article/details/85093765
https://www.cnblogs.com/Determined22/p/6750327.html
https://zhuanlan.zhihu.com/p/35620631
https://zhuanlan.zhihu.com/p/56317740
https://www.cnblogs.com/Determined22/p/6915730.html
https://zhuanlan.zhihu.com/p/63087935