論文解讀(GAN)《Generative Adversarial Networks》
Paper Information
Title:《Generative Adversarial Networks》
Authors:Ian J. Goodfellow, Jean Pouget-Abadie, M. Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron C. Courville, Yoshua Bengio
Sources:2014, NIPS
Other:26700 Citations, 41 References
Code:Download
Paper:Download
Abstract
本文提出一個 new framework , 通過一個 adversarial process 來估計生成模型。該模型同時訓練兩個模型:
-
- A generative model $G$ that captures the data distribution.
- A discriminative model $D$ that estimates the probability that a sample came from the training data rather than $G$.
Generative model $G$ 主要做的是:使得 fake sample 儘可能的欺騙 discriminative model $D$ ,使其辨別不出來。
Discriminative model $D$ 主要做的是:將 generative model $G$ 生成的 fake sample 與 true sample 識別出來。
該過程可以總結為:This framework corresponds to a minimax two-player game(minmax 雙人博弈).
模型的優點:
-
- $G$ and $D$ are defined by multilayer perceptrons, the entire system can be trained with backpropagation.
- There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of samples.
1 Introduction
- Discriminative models:Map a high-dimensional, rich sensory input to a class label.
優點:基於 backpropagation 和 dropout algorithms 取得了巨大的成功。
- Deep generative models
-
-
- 由於極大似然估計和其他方法中出現的難以計算的概率問題。
- 在 generative context 中不好利用分段線性單元的優勢。
- 由於極大似然估計和其他方法中出現的難以計算的概率問題。
-
-
- The discriminative model that learns to determine whether a sample is from the model distribution or the data distribution.
- The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency.
- Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles.
2 Related work
3 Adversarial nets
- 數據 $x$
- 基於數據 $x$ 的 generator 上的數據分布 $p_g $
- 先驗的輸入雜訊變數 $p_{z}(z) $
- 基於雜訊變數的數據空間映射表示為 $G\left(z ; \theta_{g}\right) $ ,其中 $ G$ 是具有參數 $\theta_{g}$ 的 MLP
- MLP函數:$D\left(x ; \theta_{d}\right)$ ,輸出一個標量
- 真實數據分布: $D(x) $ 表示 $x$ 來自真實數據分布而不是 $p_{g}$ 的概率。
-
- 假設判別器 $D$ 能夠正確區分來自 $\mathrm{G} $ 的生成數據和真實數據,那麼 $D(G(z))$ 應為 $0$(判別為”負”類),則 $\log (1-D(G(z))) =log(1-0) = 0 $ 。
- 假設判別器 $D$ 不能區分來自 $G $的生成數據與真實數據,最極端的情況下,把所有的數據都當作真實數據,那麼$ D(G(z))$ 為 $1$ (判別為”正”類),則 $\log (1-D(G(z))) =log(1-1) $ 是負無窮。
目標函數如下:
$\underset {G}{min}\underset {D}{max}V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\quad \quad \quad (1)$
分析上式, $x$ 是真實數據, $D(X)$ 表示給真實數據打的分數, $G(z)$ 表示生成器生成的數據, $D(G(z))$ 表示給生成數據打的分數。我 們希望 $D(x)$ 大的同時 $D(G(z)) $ 也很大。
-
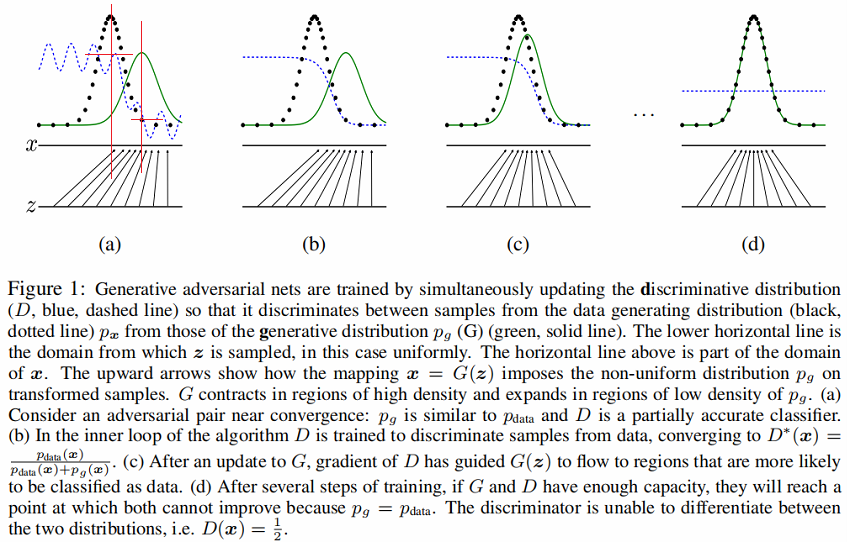
判別分布D(藍色、虛線)
-
數據生成分布 $p_x$(黑色,虛線)
-
雜訊生成分布 $P_{g}(G)$(G 綠色,實線)
-
下面的水平線為均勻取樣 $z$ 的區域,上面的水平線為 $x$ 的部分區域。
-
朝上的箭頭顯示映射 $x=G(z)$ 如何將非均勻分布 $p_{g}$ 作用在轉換後的樣本上。
-
$G$ 在 $p_{g}$ 高密度區域收縮,且在 $p_{g}$ 的低密度區域擴散。
-
Figure1 (a) 考慮一個接近收斂的對抗的模型對: $p_{g}$ 與 $p_{\text {data }}$ 分布相似,且 $D$ 是個部分準確的分類器【密度中心部分可以大致識別出來】。(可以發現$p_{g}$ 與 $p_{\text {data }}$ 的密度中心不一樣,判別器 $D$ 在 $p_{data}$ 的密度中心值高,在 $p_{g}$的密度中心值低。(紅色區域相交部分))
-
Figure1 (b) 在演算法的內循環中,訓練 $D$ 來判別數據中的樣本,收斂到:$ D^{*}(X)=\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)} $。
-
Figure1 (c) 在 G 更新後, $D$ 的梯度引導 $G(z) $ 與真實數據分布越發接近。
-
Figure1 (d) 經過若干步訓練後,如果 $G$ 和 $D$ 性能足夠,它們接近某個穩定點並都無法繼續提高性能,因為此時 $p_{g}=p_{\text {data }}$ 。判別器將無法區分訓練數據分布和生成數據分布,即 $D(x)=\frac{1}{2}$ 。
4 Theoretical Results
演算法:

4.1 Global Optimality of $p_g = p_{data}$
4.1.1 最優判別器
Proposition 1. For $G$ fixed, the optimal discriminator $D$ is
${\large D_{G}^{*}(\boldsymbol{x})=\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}} \quad \quad \quad (2)$
證明:
首先考慮將生成器 $G$ 固定, 優化最優判別器 $D$。此時最大化 $V (G, D)=V (D)$ :
$\begin{aligned}V(G, D) =V (D)&=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\&=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x\end{aligned}\quad \quad \quad (3)$
令 $p_{data}(x)$ 為 $a$,$p_{g}(x)$ 為 $b$,$D(x)$ 為 $y$。 對於任意的 $(a, b) \in \mathbb{R}^{2} \backslash\{0,0\} $,函數 $y \rightarrow a \log (y)+b \log (1-y) $ 在 $ \frac{a}{a+b}\in [0,1] $ 取最值。
請注意,$D$ 可以被解釋為條件概率 $P(Y=y \mid \boldsymbol{x})$ 的最大對數似然估計。這裡,$Y$ 代表著 $\boldsymbol{x}$ 來自 $p_{\text {data }}$ (with $y=1$ ) 或者來自 $p_{g}$ (with $y=0 $ )。
Eq. 1 可以轉換為:
$\begin{aligned}C(G) &=\max _{D} V(G, D) \\&=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{z}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\&=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\&=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]\end{aligned}\quad \quad \quad (4)$
4.1.2 最優生成器
證明:
當 $p_{g}=p_{\text {data }}$ 時,最優判別器
${\large D_{G}^{*}(\boldsymbol{x}) =\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}=\frac{1}{2}} $
此時目標函數 $V (G, D)=V (G)$
$ \begin{array}{l} V(G,D)&=V(G)\\&=\int_{x} p_{\text {data }}(x) \log \frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}+p_{g}(x) \log \left(1-\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}\right) d x\end{array} $
利用最優判別器 ${\large D_{G}^{*}(\boldsymbol{x}) =\frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}=\frac{1}{2}} $,對 $V (G)$ 做變換得:
$\begin{array}{l} V(G,D)&=V(G)\\&=-\log 2 \int_{x} p_{g}(x)+p_{\text {data }}(x) d x\\&\quad+\int_{x} p_{\text {data }}(x)\left(\log 2+\log \frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}\right)+p_{g}(x)\left(\log 2+\log \frac{p_{g}(x)}{p_{\text {data }}(x)+p_{g}(x)}\right) d x \end{array}$
其中:
$\begin{array}{l} -\log 2 \int_{x} p_{g}(x)+p_{data }(x) d x\\=-2 \log 2\int_{x} p_{data}(x)dx\\=-\log4\end{array}$
$\begin{array}{l}\log 2+\log \frac{p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}&=\log \frac{2 p_{\text {data }}(x)}{p_{\text {data }}(x)+p_{g}(x)}\\&=\log \frac{p_{\text {data }}(x)}{\left(p_{\text {data }}(x)+p_{g}(x)\right) / 2}\end{array} $
$\begin{array}{l}\log 2+\log \frac{p_{g }(x)}{p_{\text {data }}(x)+p_{g}(x)}&=\log \frac{2 p_{g }(x)}{p_{\text {data }}(x)+p_{g}(x)}\\&=\log \frac{p_{g }(x)}{\left(p_{\text {data }}(x)+p_{g}(x)\right) / 2}\end{array} $
所以,最終結果為:
$\begin{array}{l} V(G,D)&=V(G)\\&=-\log 4+D_{K L}\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_{g}}{2}\right)+\left(p_{g} \| \frac{p_{\text {data }}+p_{g}}{2}\right)\end{array}\quad \quad \quad (5)$
由於KL散度的非負性,得 $C(G)$ 的最小值為 $−\log4 $。
Tips
相對熵 (Relative Entropy) 也稱 KL 散度。在機器學習中,$P$ 往往用來表示樣本的真實分布,$Q$ 用來表示模型所預測的分布,那麼KL散度就可以計算兩個分布的差異,也就是Loss損失值。
$D_{K L}(P \| Q)=E_{p(x)}\left[\log \frac{p(x)}{q(x)}\right]=\int_{x} p(x) \log \frac{p(x)}{q(x)}$
- KL散度具有非負性。
- 當且僅當 $P$ , $Q$ 在離散型變數下是相同的分布時,即 $ p(x)=q(x)$ , $ D_{K L}(P \| Q)=0$ 。
- K L 散度衡量了兩個分布差異的程度,經常被視為兩種分布間的距離。
- 請注意, $D_{K L}(P \| Q) \neq D_{K L}(Q \| P)$ ,即 $K L$ 散度沒有對稱性。
從KL的散度定義式可以看出其值域範圍為 $[-\infty ,\infty]$ ,且不具有對稱性,所以這裡將 Eq.5. 轉變為JS散度。
$C(G)=-\log (4)+2 \cdot J S D\left(p_{data} \| p_{g}\right)\quad \quad \quad (6)$
為什麼選擇JS散度:
-
- JS散度具有非負性質
- JS散度的值域範圍在 $[0,1]$ ,$p$ 和 $q$ 分布相同的時候為 $0$,完全不同的時候為 $1$。
4.2 Convergence of Algorithm 1
Proposition 2. If $G$ and $D$ have enough capacity, and at each step of Algorithm 1, the discriminator is allowed to reach its optimum given $G $, and $p_{g}$ is updated so as to improve the criterion
$\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right]$
then $p_{g}$ converges to $p_{data }$
5 Experiments
數據集:Minist、TFD 以及 CIFAR-10。
生成器 Generator 使用的激活函數有 ReLU 和 sigmoid,判別器 Discirminator 使用的激活函數是 maxout。
Dropout 演算法被用於判別器網路的訓練。
雖然理論上可以在生成器的中間層使用 Dropout 和 其他雜訊,但這裡僅在 generator network 的最底層使用雜訊輸入。
對 $G$ 生成的樣本擬合 Gaussian Parzen window,並報告該分布下的 log-likelihood,來估計 $p_{g}$ 下測試集數據的概率。高斯分布中的參數 $\sigma$ 通過驗證集的交叉驗證得到的。
Breuleux et al.引入該過程用於不同的似然難解生成模型上,結果在 Table1 中:

我們可以看到結果中方差很大,並且在高維模型中表現不好。
在 Figures 2 和 Figures 3,我們展示了訓練後從 generator net 中提取的樣本。


6 Advantages and disadvantag
優點:無需馬爾科夫鏈,僅用反向傳播來獲得梯度,學習間無需推理,且模型中可融入多種函數。
缺點:(論文中說主要為 $p_{g}(x)$ 的隱式表示 。且訓練時 $\mathrm{G}$ 和 $\mathrm{D}$ 要同步,即訓練 $\mathrm{G}$ 後,也要訓練 $\mathrm{D} $ ,且不能將 $G$ 訓練太好而不去訓練 $D$(通俗解釋就是 $G$ 訓練的太好很容易就”欺騙”了沒訓練的 $D$)。

7 Conclusions and future work
1. A conditional generative model $p(\boldsymbol{x} \mid \boldsymbol{c})$ can be obtained by adding $\boldsymbol{c}$ as input to both $G$ and $D$ .
2. Learned approximate inference can be performed by training an auxiliary network to predict $\boldsymbol{z}$ given $\boldsymbol{x}$ . This is similar to the inference net trained by the wake-sleep algorithm but with the advantage that the inference net may be trained for a fixed generator net after the generator net has finished training.
3. One can approximately model all conditionals $p\left(\boldsymbol{x}_{S} \mid \boldsymbol{x}_{\not}\right) $ where $S$ is a subset of the indices of $x$ by training a family of conditional models that share parameters. Essentially, one can use adversarial nets to implement a stochastic extension of the deterministic MP-DBM .
4. Semi-supervised learning: features from the discriminator or inference net could improve performance of classifiers when limited labeled data is available.
5. Efficiency improvements: training could be accelerated greatly by divising better methods for coordinating $G$ and $D$ or determining better distributions to sample $\mathrm{z}$ from during training.
參考:


