矩陣旋轉-Eigen應用(QTCreator編輯器)
- 2021 年 5 月 13 日
- 筆記
一、概述
-
旋轉變換的核心思想
在不同坐標系下,雖然坐標不同,但是同一個向量還是一樣的。這句話有點兒怪怪的,但是可以用數學公式表出:\(\beta_1^T\cdot\alpha_1=\beta_2^T\cdot\alpha_2\),其中\(\beta\)是不同坐標系的標準正交基(行分塊),\(\alpha\)是不同坐標系下的坐標(列向量)。
-
旋轉變換的五種表述
- 旋轉矩陣;
- 歐式矩陣;
- 旋轉向量;
- 歐拉角;
- 四元數;
-
旋轉變換表述的演替
- 旋轉矩陣和平移矩陣:有小尾巴累積(非線性)
- 歐式矩陣:n+1維方陣要\((n+1)^2\)個自由度,太多了(線性,但不緊湊且不直觀)
- 旋轉向量:這是什麼呀這一堆數?!看不懂!(緊湊但不直觀)
- 歐拉角:這會看懂了…等等,這轉個90\(^\circ\)咋就膈屁了呢?!(緊湊直觀但奇異)
- 四元數:愛咋轉咋轉…等等不對!咋1個\(R\)冒倆\(q\)呢?\(q\)咋還內訌了呢?(緊湊非奇異,但不唯一且不穩定)
-
在Eigen庫中它們四個大哥(歐式矩陣對不起,現在我們只考慮旋轉)的轉換關係
旋轉向量和四元數先初始化(默認定義為『單位陣』,不能賦值為nullptr或者直接使用)!!!
-
旋轉矩陣
-
初始化旋轉矩陣
Eigen::Matrix3d rotation_matrix; // 通過標準輸入設備(標準輸入流)鍵入賦值 rotation_matrix << x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22; -
旋轉矩陣 \(\Longrightarrow\) 旋轉向量
// 第一種:通過構造函數(傳入一個旋轉矩陣) Eigen::AngleAxisd rotation_vector(rotation_matrix); // 第二種:首先初始化,然後通過旋轉矩陣直接賦值(重載了賦值運算符) Eigen::AngleAxisd rotation_vector; rotation_vector = rotation_matrix; // 第三種:首先初始化,然後from函數直接作用於this對象(rotation_vector) Eigen::AngleAxisd rotation_vector; rotation_vector.fromRotationMatrix(rotation_matrix); -
旋轉矩陣 \(\Longrightarrow\) 歐拉角
// (2, 1, 0)表示旋轉順序ZYX,數字越小表示優先順序越高 Eigen::Vector3d euler_angle = rotation_matrix.eulerAngles(2, 1, 0); -
旋轉矩陣 \(\Longrightarrow\) 四元數
// 第一種:通過構造函數(傳入一個旋轉矩陣) Eigen::Quaterniond quaternion(rotation_matrix); // 第二種:首先初始化,然後通過旋轉矩陣直接賦值(重載了賦值運算符) Eigen::Quaterniond quaternion; quaternion = rotation_matrix;
-
-
旋轉向量
-
初始化旋轉向量
// 通過構造函數 Eigen::AngleAxisd rotation_vector(alpha, Vector3d(x,y,z)); -
旋轉向量 \(\Longrightarrow\) 旋轉矩陣
// 第一種方法:通過構造方法傳入旋轉向量 Eigen::Matrix3d rotation_matrix(rotation_vector); // 第二種方法:首先初始化,然後通過旋轉向量直接賦值(重載了賦值運算符) Eigen::Matrix3d rotation_matrix; rotation_matrix = rotation_vector; // 第三種方法:通過matrix方法 Eigen::Matrix3d rotation_matrix = rotation_vector.matrix(); // 第四種方法:通過toRotationMatrix方法 Eigen::Matrix3d rotation_matrix = rotation_vector.toRotationMatrix(); -
旋轉向量 \(\Longrightarrow\) 歐拉角
// 不能直接轉換,需要通過旋轉矩陣搭橋 Eigen::Vector3d euler_angles = rotation_vector.matrix().eulerAngles(2, 1, 0); -
旋轉向量 \(\Longrightarrow\) 四元數
// 第一種方法:通過構造函數傳入旋轉向量 Eigen::Quaterniond quaterniond(rotation_vector); // 第二種方法:首先初始化,然後用旋轉向量賦值 Eigen::Quaterniond quaterniond; quaterniond = rotation_vector;
-
-
歐拉角
-
初始化歐拉角
Eigen::Vector3d euler_angles(yaw, pitch, roll); -
歐拉角 \(\Longrightarrow\) 旋轉矩陣
// 初始化三個旋轉角的旋轉向量 Eigen::AngleAxisd rollAngle(AngleAxisd(euler_angles(2),Eigen::Vector3d::UnitX())); Eigen::AngleAxisd pitchAngle(AngleAxisd(euler_angles(1),Eigen::Vector3d::UnitY())); Eigen::AngleAxisd yawAngle(AngleAxisd(euler_angles(0),Eigen::Vector3d::UnitZ())); // 先初始化旋轉矩陣為單位矩陣,然後這三個旋轉向量相乘得到旋轉矩陣(運算符重載) Eigen::Matrix3d rotation_matrix; rotation_matrix = yawAngle * pitchAngle * rollAngle; -
歐拉角 \(\Longrightarrow\) 旋轉向量
// 初始化三個旋轉角的旋轉向量 Eigen::AngleAxisd rollAngle(AngleAxisd(euler_angles(0), Eigen::Vector3d::UnitX())); Eigen::AngleAxisd pitchAngle(AngleAxisd(euler_angles(1), Eigen::Vector3d::UnitY())); Eigen::AngleAxisd yawAngle(AngleAxisd(euler_angles(2), Eigen::Vector3d::UnitZ())); // 先初始化旋轉向量,然後這三個旋轉向量相乘得到旋轉向量(運算符重載) Eigen::AngleAxisd rotation_vector; rotation_vector = yawAngle * pitchAngle * rollAngle; -
歐拉角 \(\Longrightarrow\) 四元數
// 初始化三個旋轉角的旋轉向量 Eigen::AngleAxisd rollAngle(AngleAxisd(euler_angles(2),Eigen::Vector3d::UnitX())); Eigen::AngleAxisd pitchAngle(AngleAxisd(euler_angles(1),Eigen::Vector3d::UnitY())); Eigen::AngleAxisd yawAngle(AngleAxisd(euler_angles(0),Eigen::Vector3d::UnitZ())); // 先初始化四元數,然後這三個旋轉向量相乘得到旋轉向量(運算符重載) Eigen::Quaterniond quaterniond; quaterniond = yawAngle * pitchAngle * rollAngle;
-
-
四元數
-
初始化四元數
Eigen::Quaterniond quaterniond(w, x, y, z); -
四元數 \(\Longrightarrow\) 旋轉矩陣
// 第一種方法:通過構造方法傳入四元數 Eigen::Matrix3d rotation_matrix(quaterniond); // 第二種方法:首先初始化,然後通過四元數直接賦值(重載了賦值運算符) Eigen::Matrix3d rotation_matrix; rotation_matrix = quaterniond; // 第三種方法:通過matrix方法 Eigen::Matrix3d rotation_matrix = quaterniond.matrix(); // 第四種方法:通過toRotationMatrix方法 Eigen::Matrix3d rotation_matrix = quaterniond.toRotationMatrix(); -
四元數 \(\Longrightarrow\) 旋轉向量
// 第一種方法:通過構造函數傳入一個四元數 Eigen::AngleAxisd rotation_vector(quaterniond); // 第二種方法:通過四元數直接賦值(運算符重載) Eigen::AngleAxisd rotation_vector; rotation_vector = quaterniond; -
四元數 \(\Longrightarrow\) 歐拉角
// 不能直接轉換,需要靠旋轉矩陣搭橋 Eigen::Vector3d euler_angles = quaterniond.matrix().eulerAngles(2, 1, 0);
-
-
在Eigen中的轉換——總結篇
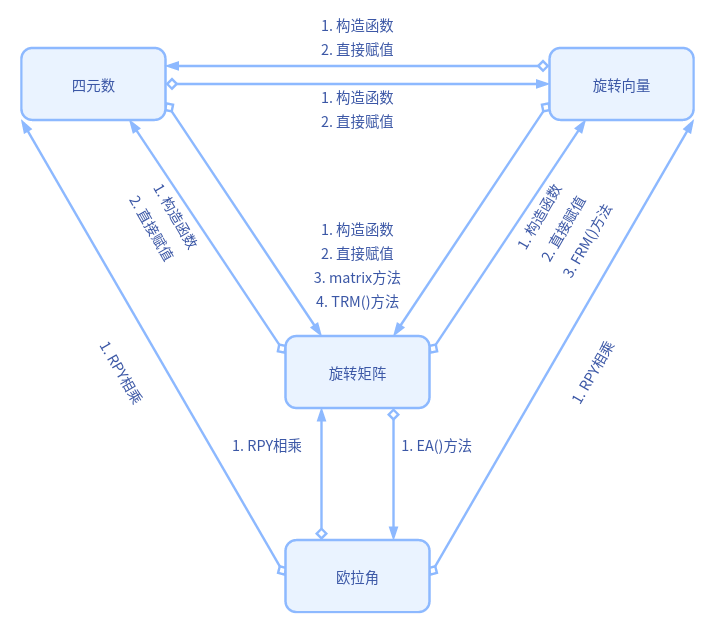
- 旋轉矩陣到旋轉向量的FRM()方法是fromRotationMatrix();
- 四元數和旋轉向量到旋轉矩陣用的同一套體系,其中TRM()方法是toRotationMatrix();
- 只有旋轉矩陣才能直接轉換為歐拉角,其EA()方法為eulerAngles();
- 歐拉角轉換成其他旋轉表述形式用的同一套體系:RPY相乘。先初始化三個旋轉角(RPY)的旋轉向量,然後初始化所需旋轉表述形式,最後這三個旋轉向量相乘得到相應旋轉表述形式(運算符重載);
-
-
旋轉表述的使用
-
旋轉矩陣
Eigen::Vector3d v( 1,0,0 ); v_rotated = rotation_matrix * v; -
歐式矩陣
Eigen::Vector3d v( 1,0,0 ); Eigen::Isometry3d T=Eigen::Isometry3d::Identity(); // 為歐式矩陣設置旋轉矩陣 T.rotate(rotation_vector); // 為歐式矩陣設置平移矩陣 T.pretranslate(Eigen::Vector3d(1, 3, 4)); Eigen::Vector3d v_transformed = T * v; -
旋轉向量
Eigen::Vector3d v( 1,0,0 ); Eigen::Vector3d v_rotated = rotation_vector * v; -
歐拉角
Eigen::Vector3d v( 1,0,0 ); Eigen::Vector3d euler_angles(M_PI / 4, M_PI / 4, M_PI / 4); // 通過上述轉換:rotation_matrix !!! Eigen::Vector3d v_rotated = rotation_matrix * v; -
四元數
Eigen::Vector3d v( 1,0,0 ); Eigen::Quaterniond q = Eigen::Quaterniond(rotation_vector); // 注意數學上的表達式是:qvq^{-1} Eigen::Vector3d v_rotated = q * v;
-
二、詳述
-
旋轉矩陣
-
旋轉矩陣的定義
\[\begin{aligned}
&由旋轉的本質方程:\beta_1^T\alpha_1=\beta_2^T\alpha_2,
又由於\beta是標準正交基,所以\beta\beta^T = E;
\\
&所以兩邊同時乘上\beta_1,故而可得\alpha_1=\beta_1\beta_2^T\alpha_2,記旋轉矩陣R=\beta_1\beta_2^T;
\end{aligned}
\] -
旋轉矩陣各個參數的意義
\(\beta\)是標準正交基,\(\alpha\)是相應坐標系下的坐標。
-
旋轉矩陣各個參數的計算
\(R=\beta_1\beta_2^T\)。
-
-
歐式矩陣
-
歐式矩陣的定義
\[T =
\left[
\begin{matrix}
R&t\\
\it{0}^T&1
\end{matrix}
\right]
\] -
歐式矩陣各個參數的意義
\(R\)是旋轉矩陣,\(t\)是平移向量,\(\it{0}^T\)是0列向量。
-
歐式矩陣各個參數的計算
不用計算,直接就有!!!
-
-
旋轉向量
-
旋轉向量的定義
\[\overrightarrow{n}與旋角\theta
\] -
旋轉向量各個參數的意義
任何一個向量(或稱為點)【1】的旋轉都是繞著一個特定的軸來旋轉,我們可以用這個軸的長度保存旋轉角的大小\(\theta\)。故而旋轉角被定義為:\(\theta\overrightarrow{n}\)。
【注】【1】:這裡本來是坐標系的旋轉,但是我們用相對的眼光看問題,我們如果聚焦於坐標系的話就相當與是向量在旋轉。一個向量繞著一個軸在轉可能比坐標系繞著一個軸在轉好理解一點,這倆本質一樣。
-
旋轉向量各個參數的計算
-
旋轉軸\(\overrightarrow{n}\)的計算
旋轉軸在旋轉的時候是不會變化的,所以有:\(R\overrightarrow{n}=\overrightarrow{n}\),即有\(\overrightarrow{n}\)為\(R\)的特徵值為1的特徵向量。
-
旋轉角\(\theta\)的計算
羅德格里斯指出了旋轉向量到旋轉矩陣的法則:\(R=\cos{\theta}I+(1-\cos{\theta})\overrightarrow{n}\overrightarrow{n}^T+\sin{\theta}\overrightarrow{n}^{\wedge}\)。
同時取跡可得:\(\mathbf{tr}(R)=1+2\cos{\theta}\)。所以就計算出了\(\theta=\arccos{\frac{\mathbf{tr}(R)-1}{2}}\)。
-
-
-
歐拉角
-
歐拉角的定義
每個軸旋轉一個特定的角度,但是有順序要求,我們一般使用ZYX的順序(稱為RPY)。
-
歐拉角各個參數的意義
-
R:Roll,偏航角
-
P:Pitch,翻滾角
-
Y:Yaw,俯仰角
-
-
歐拉角各個參數的計算
通過感測器或者人為給出。不是吧不是吧,不會真有人用歐拉角吧?!【1】
【注】【1】:萬向鎖問題(奇異性)問題——只要我們想用3個實數來表達3維旋轉時,都會不可避免地碰到奇異性問題。所以很少用這樣的旋轉表述方式,一般用也只是用於人機交互中傳入旋轉角度,或者驗證系統的演算法,因為這樣的表述對於人類來說是非常直觀的。
-
-
四元數
-
四元數的定義
\[q=(s,\overrightarrow{v})^{T}=(s,x,y,z)^{T}=s+xi+yj+zk
\] -
四元數各個參數的意義
-
實部\(s\)表示旋轉程度:\(s=f(\theta)\);
-
虛部\(\overrightarrow{v}\)表示旋轉軸:\(\overrightarrow{v}=k\overrightarrow{n}\);
虛部\(\overrightarrow{v}\)的定義為某個點在三維直角系下的坐標,由於四元數表示對一個向量(或稱為點)的旋轉,用數學公式可以嚴謹地證明,當對\(\overrightarrow{v}\)進行\(q=(s,\overrightarrow{v})^{T}\)旋轉時不變,所以\(\overrightarrow{v}\)表示旋轉軸。
-
-
四元數各個參數的計算(利用旋轉向量)
-
實部\(s\)的計算
-
四元數 \(\Longrightarrow\) 旋轉矩陣
\[\begin{aligned}
R& = \overrightarrow{v}\overrightarrow{v}^{T}+s^2I+2s\overrightarrow{v}^{\wedge}+(\overrightarrow{v})^2
\\\\
\mathbf{tr}(R)&=4s^2-1
\end{aligned}
\] -
旋轉矩陣 \(\Longrightarrow\) 旋轉向量
\[\begin{aligned}
\theta& = \arccos(\frac{\mathbf{tr}(R)-1}{2})=\arccos(2s^2-1)
\\\\
\theta& = 2\arccos{s}
\\\\
s& = \cos{\frac{\theta}{2}}
\end{aligned}
\]
-
-
虛部\(\overrightarrow{v}\)的計算
-
得到旋轉軸
旋轉軸就是四元數的虛部\(\overrightarrow{v}\)。
-
將四元數單位化
我們已經知道了實部\(s=\cos{\frac{\theta}{2}}\),所以虛部向量就只用除以一個\(\sin{\frac{\theta}{2}}\)就行了。
-
-
-


