邏輯回歸(Logistic Regression)詳解,公式推導及程式碼實現
- 2019 年 10 月 3 日
- 筆記
邏輯回歸(Logistic Regression)
什麼是邏輯回歸:
邏輯回歸(Logistic Regression)是一種基於概率的模式識別演算法,雖然名字中帶”回歸”,但實際上是一種分類方法,在實際應用中,邏輯回歸可以說是應用最廣泛的機器學習演算法之一
回歸問題怎麼解決分類問題?
將樣本的特徵和樣本發生的概率聯繫起來,而概率是一個數.換句話說,我預測的是這個樣本發生的概率是多少,所以可以管它叫做回歸問題
在許多機器學習演算法中,我們都是在追求這樣的一個函數
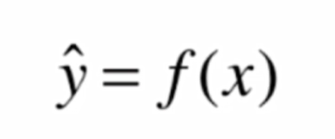
例如我們希望預測一個學生的成績y,將現有數據x輸入模型 f(x) 中,便可以得到一個預測成績y
但是在邏輯回歸中,我們得到的y的值本質是一個概率值p
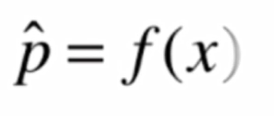
在得到概率值p之後根據概率值來進行分類
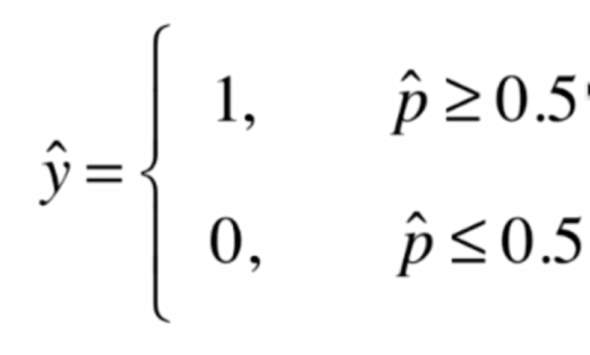
當然了這個1和0在不同情況下可能有不同的含義,比如0可能代表惡性腫瘤患者,1代表良性腫瘤患者
邏輯回歸既可以看做是回歸演算法,也可以看做是分類演算法,通常作為分類演算法用,只可以解決二分類問題,不過我們可以使用一些其他的技巧(OvO,OvR),使其支援解決多分類問題
下面我們來看一下邏輯回歸使用什麼樣的方法來得到一個事件發生的概率的值
在線性回歸中,我們使用
![]()
來計算,要注意,因為Θ0的存在,所以x用小的Xb來表示,就是每來一個樣本,前面還還要再加一個1,這個1和Θ0相乘得到的是截距,但是不管怎樣,這種情況下,y的值域是(-infinity, +infinity)
而對於概率來講,它有一個限定,其值域為[0,1]
所以我們如果直接使用線性回歸的方式,去看能不能找到一組Θ來與特徵x相乘之後得到的y值就來表達這個事件發生的概率呢?
其實單單從應用的角度來說,可以這麼做,但是這麼做不夠好,就是因為概率有值域的限制,而使用線性回歸得到的結果則沒有這個限制
為此,我們有一個很簡單的解決方案:
我們將線性回歸得到的結果再作為一個特徵值傳入一個新的函數,經過轉換,將其轉換成一個值域在[0,1]之間的值
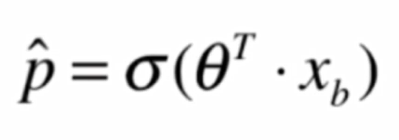
Sigmoid函數:

將函數繪製出來:
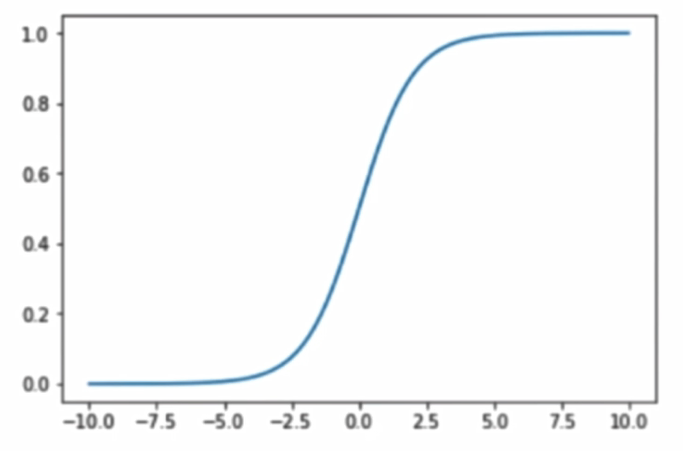
其最左端趨近於0,最右端趨近於1,其值域在(0,1),這正是我們所需要的性質
當傳入的參數 t > 0 時, p > 0.5, t < 0 時, p < 0.5,分界點是 t = 0
使用Sigmoid函數後:


現在的問題就是,給定了一組樣本數據集X和它對應的分類結果y,我們如何找到參數Θ,使得用這樣的方式可以最大程度的獲得這個樣本數據集X對應的分類輸出y
這就是我們在訓練的過程中要做的主要任務,也就是擬合我們的訓練樣本,而擬合過程,就會涉及到邏輯回歸的損失函數
邏輯回歸的損失函數:

我們定義了一個這樣的損失函數:
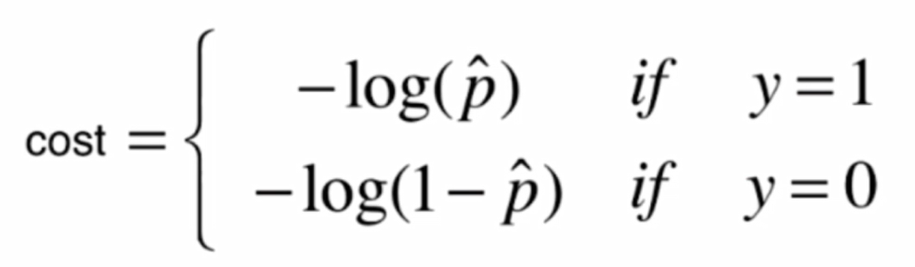
畫出影像:
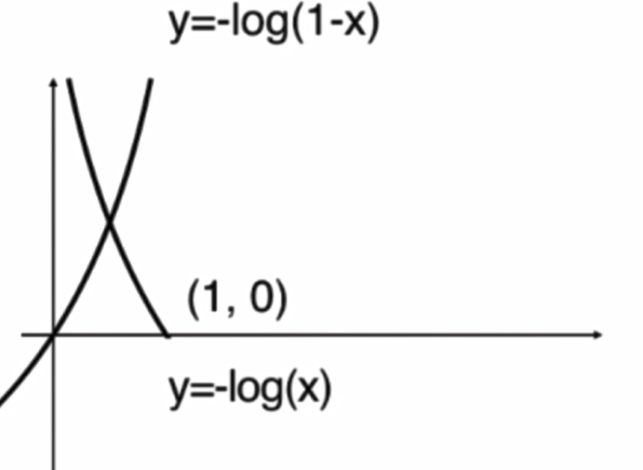
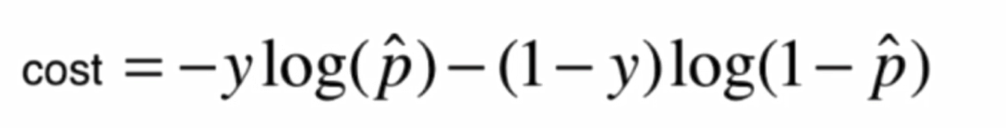
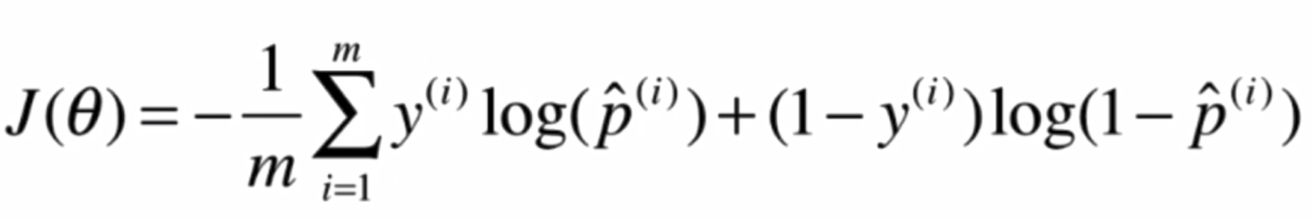
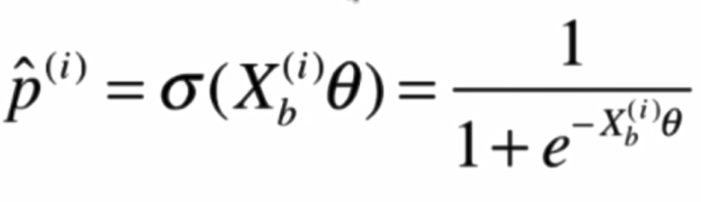
將兩個式子整合:
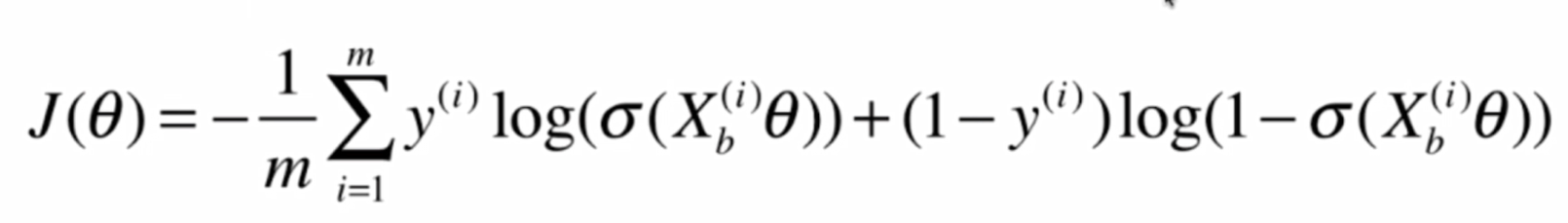
下面我們要做的事情,就是找到一組Θ,使得J(Θ)最小
對於這個式子,我們很難像線性回歸那樣推得一個正規方程解,實際上這個式子是沒有數學解的,也就是無法把X和直接套進公式獲得Θ
不過,我們可以使用梯度下降法求得它的解,而且,這個損失函數是一個凸函數,不用擔心局部最優解的,只存在全局最優解
現在,我們的任務就是求出J(Θ)的梯度,使用梯度下降法來進行計算
首先,求J(Θ)的梯度的公式:

首先,我們對Sigmoid函數求導:
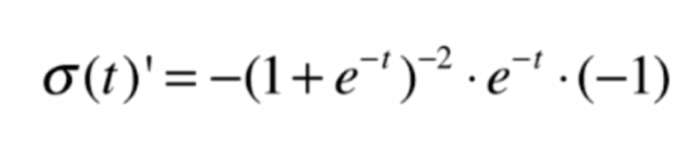
![]()
得到其導數,再對logσ(t)求導,求導步驟:
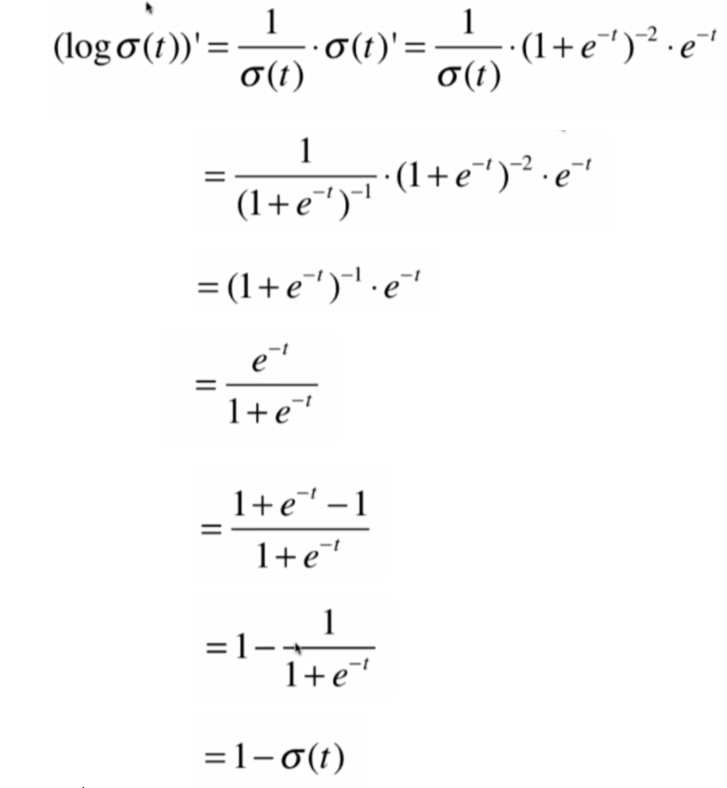
由此可知, 前半部分的導數:
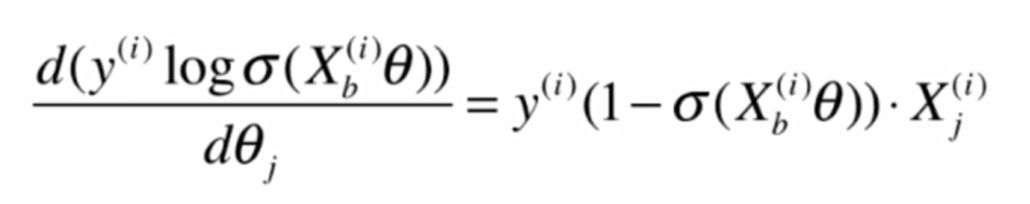
其中y(i)是常數
再求後半部分:
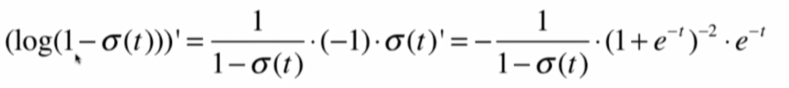
這其中
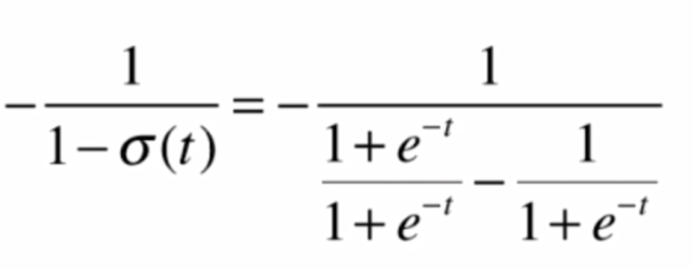
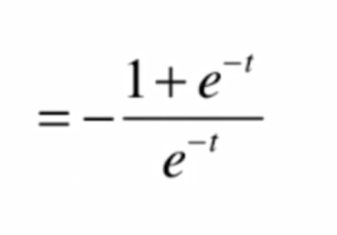
將結果代入,化簡得:
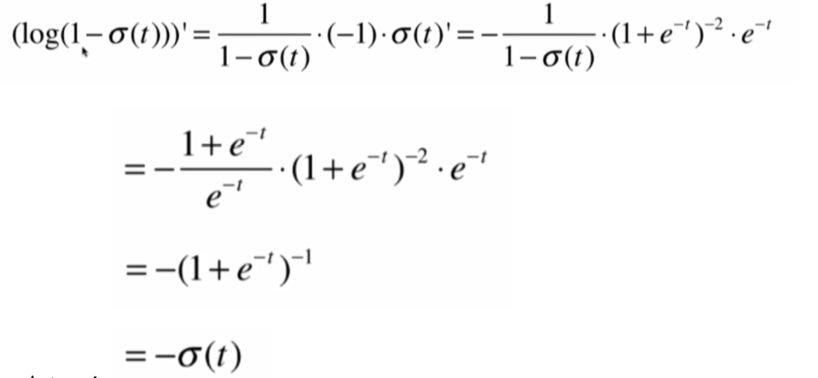
就得到後半部分的求導結果:
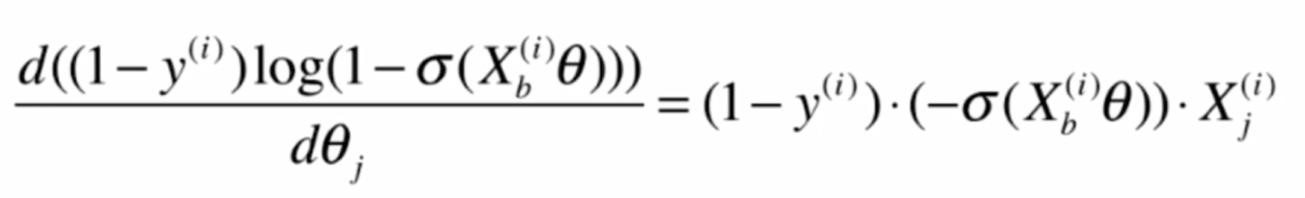
將前後部分相加:
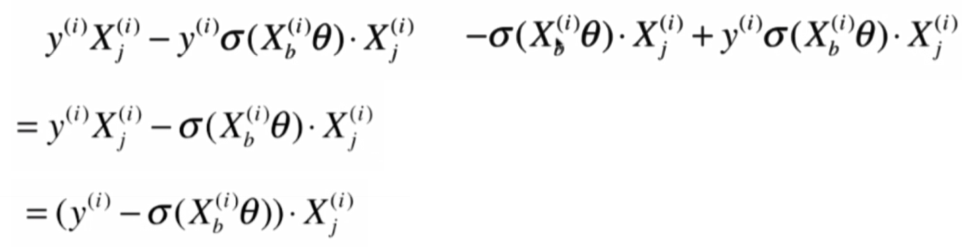
即:
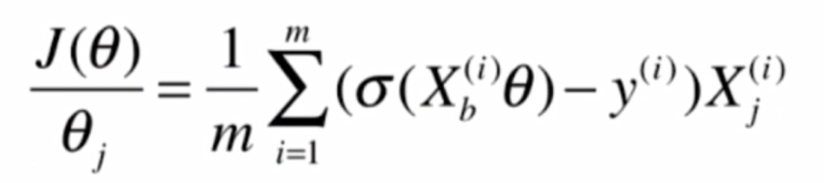
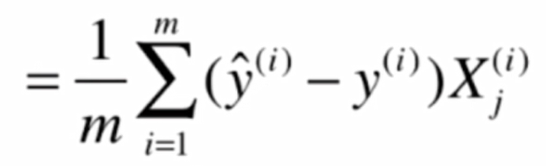
就可以得到:
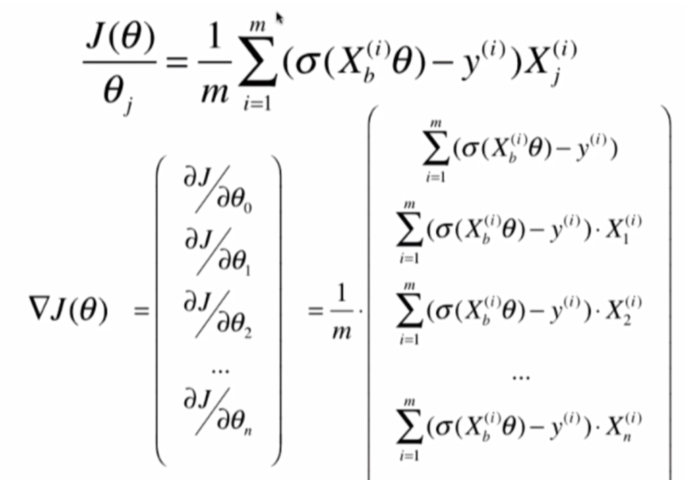
此時我們回憶一下線性回歸的向量化過程

參考這個,可以得到:

這就是我們要求的梯度,再使用梯度下降法,就可以求得結果
決策邊界:
這裡引入一個概念,叫做判定邊界,可以理解為是用以對不同類別的數據分割的邊界,邊界的兩旁應該是不同類別的數據
從二維直角坐標系中,舉幾個例子,大概是如下這個樣子:
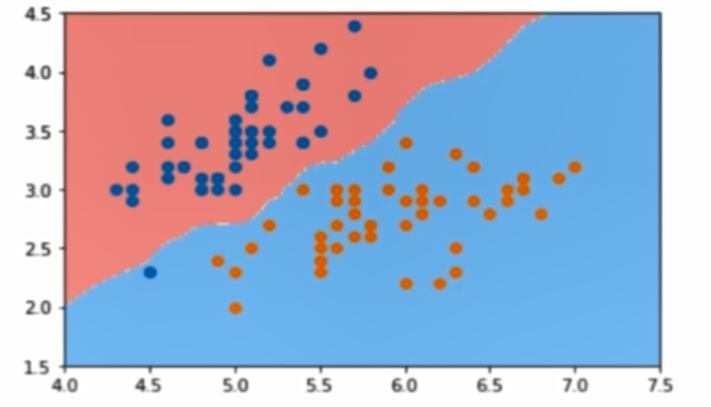
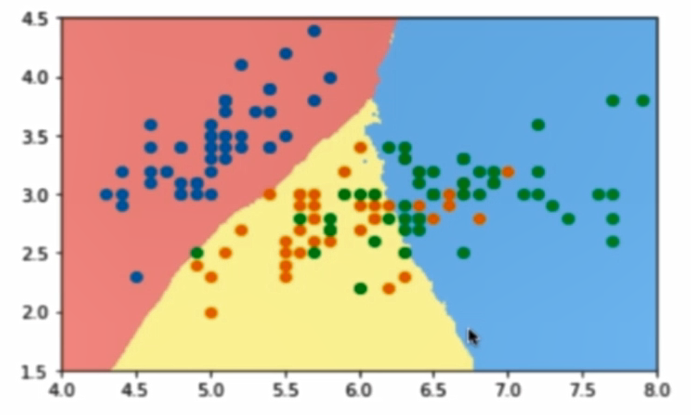
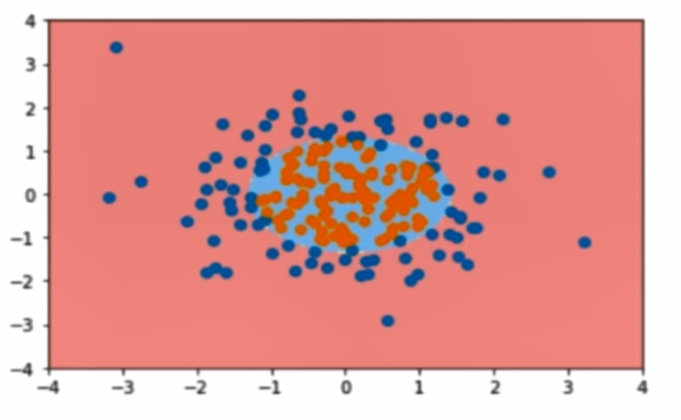
使用OvR和OvO方法解決多分類:
原本的邏輯回歸只能解決雙分類問題,但我們可以通過一些方法,讓它支援多分類問題,比如OvR和OvO方法
OvR:
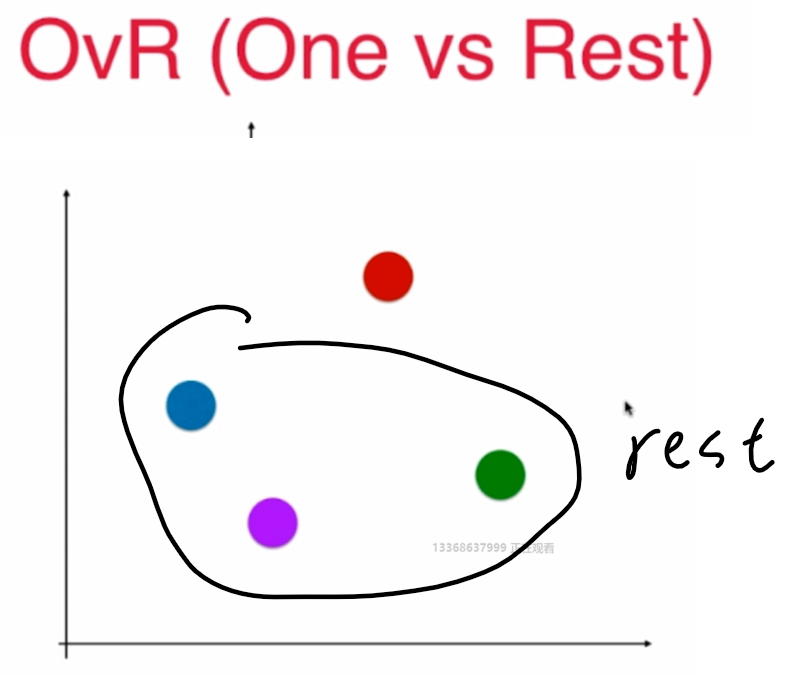
n 種類型的樣本進行分類時,分別取一種樣本作為一類,將剩餘的所有類型的樣本看做另一類,這樣就形成了 n 個二分類問題,使用邏輯回歸演算法對 n 個數據集訓練出 n 個模型,將待預測的樣本傳入這 n 個模型中,所得概率最高的那個模型對應的樣本類型即認為是該預測樣本的類型

n個類別就進行n次分類,選擇分類得分最高的
OvO:

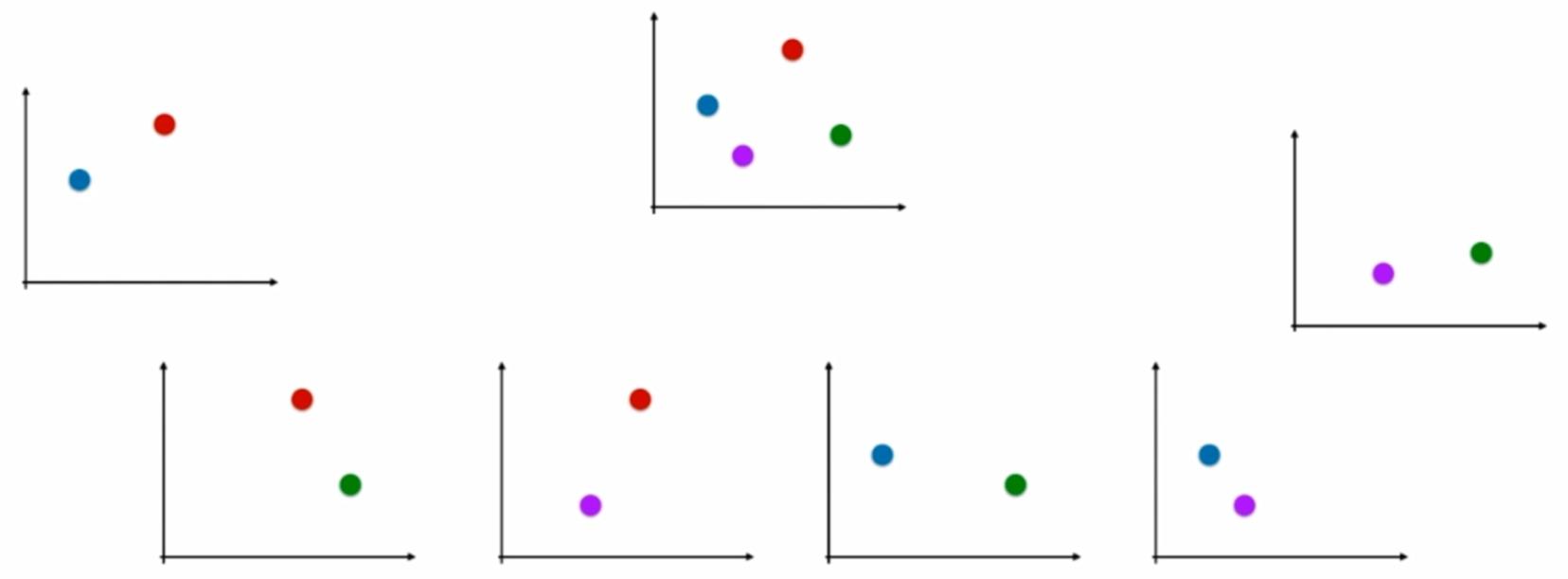
n 類樣本中,每次挑出 2 種類型,兩兩結合,一共有 Cn2 種二分類情況,使用 Cn2 種模型預測樣本類型,有 Cn2 個預測結果,種類最多的那種樣本類型,就認為是該樣本最終的預測類型
這兩種方法中,OvO的分類結果更加精確,因為每一次二分類時都用真實的類型進行比較,沒有混淆其它的類別,但時間複雜度較高
程式碼實現 :
1 import numpy as np 2 from .metrics import accuracy_score 3 4 5 class LogisticRegression: 6 7 def __init__(self): 8 """初始化Linear Regression模型""" 9 self.coef_ = None 10 self.intercept_ = None 11 self._theta = None 12 13 def _sigmoid(self, t): 14 return 1. / (1. + np.exp(-t)) 15 16 def fit(self, X_train, y_train, eta=0.01, n_iters=1e4): 17 """根據訓練數據集X_train, y_train, 使用梯度下降法訓練Logistic Regression模型""" 18 assert X_train.shape[0] == y_train.shape[0], 19 "the size of X_train must be equal to the size of y_train" 20 21 def J(theta, X_b, y): 22 y_hat = self._sigmoid(X_b.dot(theta)) 23 try: 24 return - np.sum(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) / len(y) 25 except: 26 return float('inf') 27 28 def dJ(theta, X_b, y): 29 return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b) 30 31 def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8): 32 33 theta = initial_theta 34 cur_iter = 0 35 36 while cur_iter < n_iters: 37 gradient = dJ(theta, X_b, y) 38 last_theta = theta 39 theta = theta - eta * gradient 40 if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon): 41 break 42 43 cur_iter += 1 44 45 return theta 46 47 X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) 48 initial_theta = np.zeros(X_b.shape[1]) 49 self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters) 50 51 self.intercept_ = self._theta[0] 52 self.coef_ = self._theta[1:] 53 54 return self 55 56 57 58 def predict_proba(self, X_predict): 59 """給定待預測數據集X_predict,返回表示X_predict的結果概率向量""" 60 assert self.intercept_ is not None and self.coef_ is not None, 61 "must fit before predict!" 62 assert X_predict.shape[1] == len(self.coef_), 63 "the feature number of X_predict must be equal to X_train" 64 65 X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict]) 66 return self._sigmoid(X_b.dot(self._theta)) 67 68 def predict(self, X_predict): 69 """給定待預測數據集X_predict,返回表示X_predict的結果向量""" 70 assert self.intercept_ is not None and self.coef_ is not None, 71 "must fit before predict!" 72 assert X_predict.shape[1] == len(self.coef_), 73 "the feature number of X_predict must be equal to X_train" 74 75 proba = self.predict_proba(X_predict) 76 return np.array(proba >= 0.5, dtype='int') 77 78 def score(self, X_test, y_test): 79 """根據測試數據集 X_test 和 y_test 確定當前模型的準確度""" 80 81 y_predict = self.predict(X_test) 82 return accuracy_score(y_test, y_predict) 83 84 def __repr__(self): 85 return "LogisticRegression()"
