ssd原理及程式碼實現詳解

• 2019 年 10 月 29 日
• 筆記

通過https://github.com/amdegroot/ssd.pytorch,結合論文https://arxiv.org/abs/1512.02325來理解ssd.

ssd由三部分組成:

• base
• extra
• predict
  base原論文里用的是vgg16去掉全連接層.
  
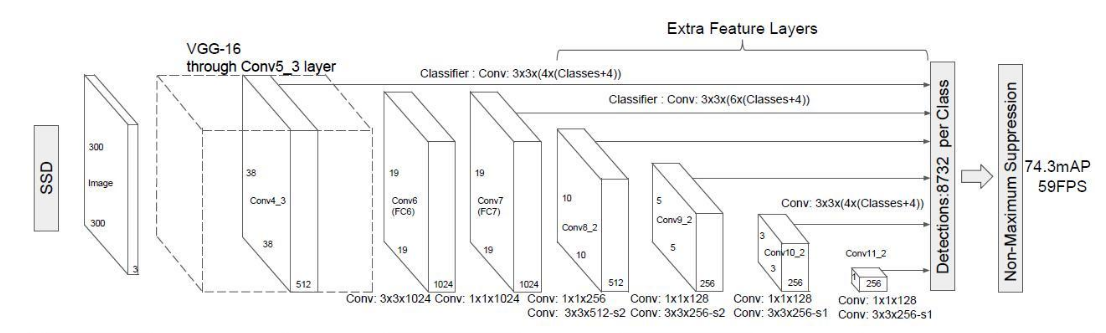
  base + extra完成特徵提取的功能.得到不同size的feature map,基於這些feature maps,我們再用不同的卷積核去卷積,分別完成類別預測和坐標預測.

基礎特徵提取網路

特徵提取網路由兩部分組成

• vgg16
• extra layer

vgg16變種

vgg16結構:

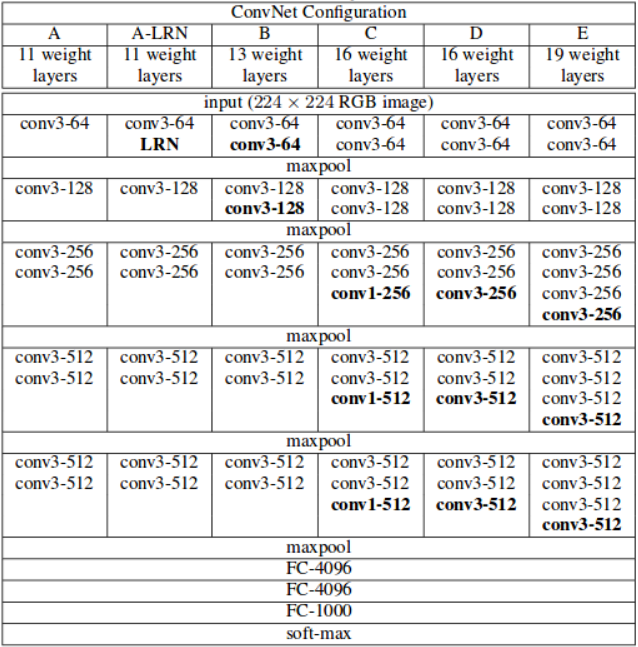
將vgg16的全連接層用卷積層換掉.

程式碼實現

ssd.py中

base = {      '300': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'C', 512, 512, 512, 'M',              512, 512, 512],      '512': [],  }  extras = {      '300': [256, 'S', 512, 128, 'S', 256, 128, 256, 128, 256],      '512': [],  }  }

定義了每一層的卷積核的數量.其中’M’,’C’均代表maxpool池化層.只是’C’會使用 ceil instead of floor to compute the output shape.
參見https://pytorch.org/docs/stable/nn.html#maxpool2d

def vgg(cfg, i, batch_norm=False):      layers = []      in_channels = i      for v in cfg:          if v == 'M':              layers += [nn.MaxPool2d(kernel_size=2, stride=2)]          elif v == 'C':              layers += [nn.MaxPool2d(kernel_size=2, stride=2, ceil_mode=True)]          else:              conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)              if batch_norm:                  layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]              else:                  layers += [conv2d, nn.ReLU(inplace=True)]              in_channels = v      pool5 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)      conv6 = nn.Conv2d(512, 1024, kernel_size=3, padding=6, dilation=6)      conv7 = nn.Conv2d(1024, 1024, kernel_size=1)      layers += [pool5, conv6,                 nn.ReLU(inplace=True), conv7, nn.ReLU(inplace=True)]      return layers  

這樣就形成了一個基礎的特徵提取網路.前面的部分和vgg16一樣的,全連接層換成了conv6+relu+conv7+relu.

extra layer

在前面得到的輸出的基礎上,繼續做卷積,以得到更多不同尺寸的feature map.

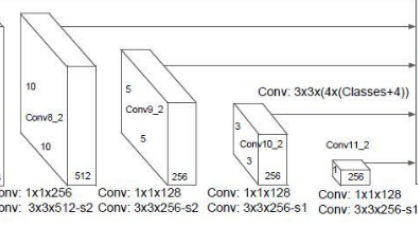
程式碼實現

extras = {      '300': [256, 'S', 512, 128, 'S', 256, 128, 256, 128, 256],      '512': [],  }    def add_extras(cfg, i, batch_norm=False):      # Extra layers added to VGG for feature scaling      layers = []      in_channels = i      flag = False      for k, v in enumerate(cfg):          if in_channels != 'S':              if v == 'S':                  layers += [nn.Conv2d(in_channels, cfg[k + 1],                             kernel_size=(1, 3)[flag], stride=2, padding=1)]              else:                  layers += [nn.Conv2d(in_channels, v, kernel_size=(1, 3)[flag])]              flag = not flag          in_channels = v      return layers    add_extras(extras[str(size)], 1024)

[256, ‘S’, 512, 128, ‘S’, 256, 128, 256, 128, 256]用以創建layer.
如果是’S’的話,代表用的卷積核為3 x 3,否則為1 x 1,卷積核的數量為’S’下一個的數字.

這樣的話,我們就構建出了extra layers.

多尺度檢測multibox

我們已經得到了很多layer的輸出(稱其為feature map).size有大有小. 那麼現在我們就對某些層(conv4_3,conv7,conv8_2,conv9_2,conv10_2,conv11_2)的feature map再做卷積,得到類別和位置資訊.
分別用2組3 x 3的卷積核去做卷積,一個負責預測類別,一個負責預測位置.卷積核的個數分別為boxnum x clasess_num,boxnum x 4(坐標由4個參數,中心坐標,box寬高即可確定).

即在m x m的feature map上做卷積我們會得到一個m x m x (boxnum x clasess_num) 和一個m x m x (boxnum x 4)的tensor.分別用以計算概率和框的位置.

程式碼實現

def multibox(vgg, extra_layers, cfg, num_classes):      loc_layers = []      conf_layers = []      vgg_source = [21, -2]      for k, v in enumerate(vgg_source):          loc_layers += [nn.Conv2d(vgg[v].out_channels,                                   cfg[k] * 4, kernel_size=3, padding=1)]          conf_layers += [nn.Conv2d(vgg[v].out_channels,                          cfg[k] * num_classes, kernel_size=3, padding=1)]      for k, v in enumerate(extra_layers[1::2], 2):          loc_layers += [nn.Conv2d(v.out_channels, cfg[k]                                   * 4, kernel_size=3, padding=1)]          conf_layers += [nn.Conv2d(v.out_channels, cfg[k]                                    * num_classes, kernel_size=3, padding=1)]      return vgg, extra_layers, (loc_layers, conf_layers)

其中每一個feature map預測幾個box由下面變數給出.

mbox = {      '300': [4, 6, 6, 6, 4, 4],  # number of boxes per feature map location      '512': [],  }

在哪些layer的feature map上做預測,根據論文里是固定的,參見開頭的ssd結構圖.反映到程式碼里則為

vgg_source = [21, -2]  extra_layers[1::2]

即
中的conv4_3,conv7,conv8_2,conv9_2,conv10_2,conv11_2這六個layer的feature map.

先驗框生成

你可以稱之為priorbox/default box/anchor box都是一個意思.
我們先來講先驗框的原理.這個其實類似yolov3中的anchor box,我們基於這些shape的box去做預測.

priorbox和不同的feature map上做預測都是為了解決對不同尺寸的物體的檢測問題.不同的feature map負責不同尺寸的目標.同時每一個feature map cell又負責該尺寸的不同寬高比的目標.

首先,不同的feature_map負責不同的尺寸.
[s_k = s_{min} + frac{s_{max} – s_{min}}{m-1}(k-1), kin [1,m]]
對smin=0.2,smax=0.9.m=6(我們在6個layer的feature map上做檢測), 因此就有 s={0.2,0.34,0.48,0.62,0.76,0.9}.
假設寬高比分別為(a_r ={1,2,3,1/2,1/3}),則對第二個feature map(19 x 19的這個,conv7),那麼[w_k^a = s_ksqrt{a_r},h_k^a = s_k/sqrt{a_r}],我們計算寬高比為1的box,則得到的box為(0.2,0.2).模型的輸入影像尺寸是(300,300),那麼相應的box為(60,60).依次類推,可以得到其餘的deafult box的shape共6個.(對寬高比為1的box,額外多計算一個(s_k^prime)的box出來). 從而我們得到了這一個feature map負責預測的不同形狀的box

如圖:

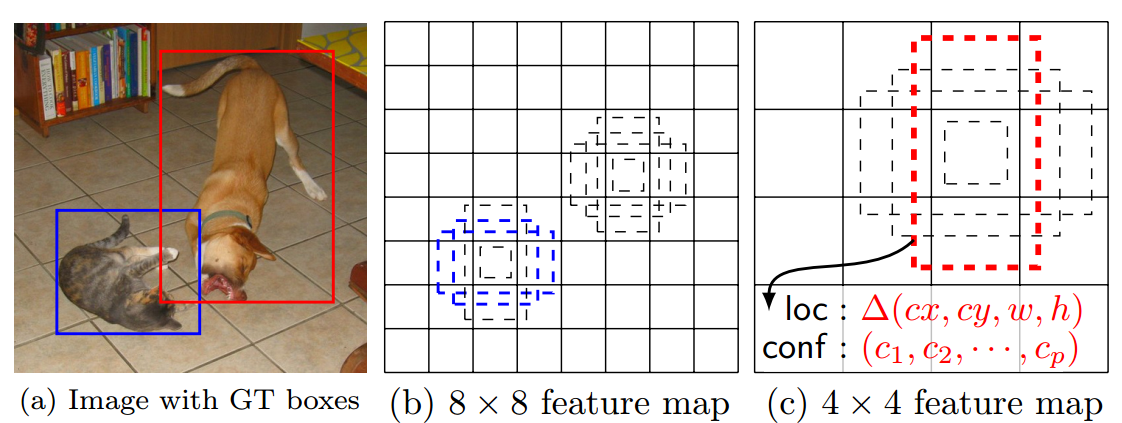
那麼對於conv4_3這個layer而言的話,我們設定的deafault box數量是4,於是我們最終就有38 x 38 x 4個box.我們在這些box的基礎上去預測我們的box.

我們對不同層的default box的數量設定是(4, 6, 6, 6, 4, 4),所以我們最終總共預測出(38^2 times 4+19^2 times 6+ 10^2 times 6+5^2 times 6+3^2 times 4+1^2 times 4 = 8732)個box.

那實際調參的重點也就是這些default box的調整,要盡量使其貼合你自己要檢測的目標.,類似於yolov3中調參調整anchor的大小.

程式碼實現

prior_box.py中定義了PriorBox類,forward函數實現default box的計算.
配置文件定義域config.py

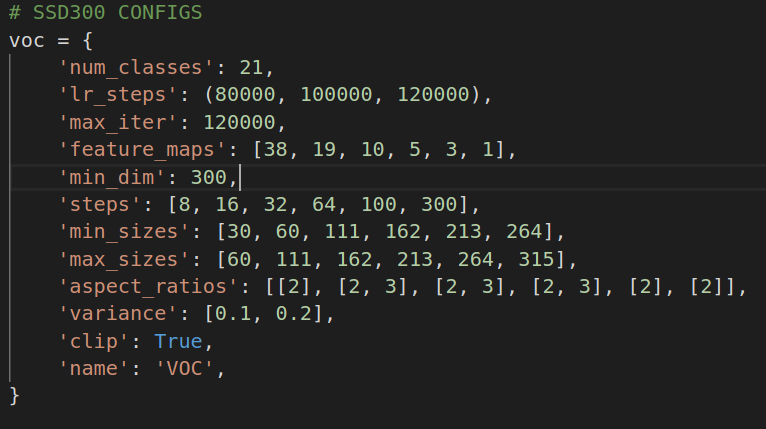
其中

    'min_sizes': [30, 60, 111, 162, 213, 264],      'max_sizes': [60, 111, 162, 213, 264, 315],      'aspect_ratios': [[2], [2, 3], [2, 3], [2, 3], [2], [2]],

用以計算每一個feature map的default box. 這裡配置文件的定義讓人稍微有點糊塗. min_size/max_size都是用於寬高比為1的box的預測.[2]用於預測寬高比為2:1和1:2的box.

    def forward(self):          mean = []          for k, f in enumerate(self.feature_maps):  #config.py中'feature_maps': [38, 19, 10, 5, 3, 1]              for i, j in product(range(f), repeat=2):                  f_k = self.image_size / self.steps[k]  #基本上除下來和feature_map size類似. 這裡直接用f替代f_k區別不大                  # unit center x,y            # 每個feature_map cell的中心                  cx = (j + 0.5) / f_k                  cy = (i + 0.5) / f_k                    # aspect_ratio: 1                  # rel size: min_size                  s_k = self.min_sizes[k]/self.image_size  #min_sizes預測一個寬高比為1的shape                  mean += [cx, cy, s_k, s_k]                    # aspect_ratio: 1                  # rel size: sqrt(s_k * s_(k+1))                  s_k_prime = sqrt(s_k * (self.max_sizes[k]/self.image_size)) #max_size負責預測一個寬高比為1的shape                  mean += [cx, cy, s_k_prime, s_k_prime]                    # rest of aspect ratios #                  for ar in self.aspect_ratios[k]:         #比如對[2,3]則預測4個shape,1;2,2:1,1:3,3:1                      mean += [cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]                      mean += [cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]

比如對38 x 38這個feature map的第一個cell,共計算出4個default box.前兩個參數是box中點,後面是寬,高.都是相對原圖的比例.

tensor([[0.0133, 0.0133, 0.1000, 0.1000],          [0.0133, 0.0133, 0.1414, 0.1414],          [0.0133, 0.0133, 0.1414, 0.0707],          [0.0133, 0.0133, 0.0707, 0.1414]])

預測框生成

feature_map卷積後的tensor含義

每一個feature_map卷積後可得一個m x m x 4的tensor.其中4是(t_x,t_y,t_w,t_h),這時候我們需要用這些數在default box的基礎上去得到我們的預測框的坐標.可以認為神經網路預測得到的是相對參考框的偏移. 這也是所謂的把坐標預測當做回歸問題的含義.box=anchor_box x 形變矩陣,我們回歸的就是這個形變矩陣的參數,即(t_x,t_y,t_w,t_h)
即

               b_center_x = t_x *prior_variance[0]* p_width + p_center_x                 b_center_y = t_y *prior_variance[1] * p_height + p_center_y                 b_width = exp(prior_variance[2] * t_w) * p_width                 b_height = exp(prior_variance[3] * t_h) * p_height  或者                   b_center_x = t_x * p_width + p_center_x                 b_center_y = t_y * p_height + p_center_y                 b_width = exp(t_w) * p_width                 b_height = exp(t_h) * p_height  

其中p_*代表的是default box. b_*才是我們最終預測的box的坐標.

這時候我們得到了很多很多(8732)個box.我們要從這些box中篩選出我們最終給出的box.
偽程式碼為

for every conv box:      for every class :          if class_prob < theshold:              continue          predict_box = decode(convbox)            nms(predict_box) #去除非常接近的框

程式碼實現

detection.py

class Detect(Function):          def forward(self, loc_data, conf_data, prior_data):          ##loc_data [batch,8732,4]          ##conf_data [batch,8732,1+class]          ##prior_data [8732,4]            num = loc_data.size(0)  # batch size          num_priors = prior_data.size(0)          output = torch.zeros(num, self.num_classes, self.top_k, 5)          conf_preds = conf_data.view(num, num_priors,                                      self.num_classes).transpose(2, 1)            # Decode predictions into bboxes.          for i in range(num):              decoded_boxes = decode(loc_data[i], prior_data, self.variance)              # For each class, perform nms              conf_scores = conf_preds[i].clone()                for cl in range(1, self.num_classes):                  c_mask = conf_scores[cl].gt(self.conf_thresh)                  scores = conf_scores[cl][c_mask]                  if scores.size(0) == 0:                      continue                  l_mask = c_mask.unsqueeze(1).expand_as(decoded_boxes)                  boxes = decoded_boxes[l_mask].view(-1, 4)                  # idx of highest scoring and non-overlapping boxes per class                  ids, count = nms(boxes, scores, self.nms_thresh, self.top_k)                  output[i, cl, :count] =                       torch.cat((scores[ids[:count]].unsqueeze(1),                                 boxes[ids[:count]]), 1)          flt = output.contiguous().view(num, -1, 5)          _, idx = flt[:, :, 0].sort(1, descending=True)          _, rank = idx.sort(1)          flt[(rank < self.top_k).unsqueeze(-1).expand_as(flt)].fill_(0)          return output      

具體的核心邏輯在box_utils.py

• decode 用於根據卷積結果計算box坐標

def decode(loc, priors, variances):      boxes = torch.cat((          priors[:, :2] + loc[:, :2] * variances[0] * priors[:, 2:],          priors[:, 2:] * torch.exp(loc[:, 2:] * variances[1])), 1)      boxes[:, :2] -= boxes[:, 2:] / 2      boxes[:, 2:] += boxes[:, :2]      return boxes

這裡做了一個center_x,center_y, w, h -> xmin, ymin, xmax, ymax的轉換.

    boxes[:, :2] -= boxes[:, 2:] / 2      boxes[:, 2:] += boxes[:, :2]

返回的已經是(xmin, ymin, xmax, ymax)的形式來表示box了.

• nms 如果兩個框的overlap超過0.5,則認為框的是同一個物體,只保留概率更高的框

def nms(boxes, scores, overlap=0.5, top_k=200):      """Apply non-maximum suppression at test time to avoid detecting too many      overlapping bounding boxes for a given object.      Args:          boxes: (tensor) The location preds for the img, Shape: [num_priors,4].          scores: (tensor) The class predscores for the img, Shape:[num_priors].          overlap: (float) The overlap thresh for suppressing unnecessary boxes.          top_k: (int) The Maximum number of box preds to consider.      Return:          The indices of the kept boxes with respect to num_priors.      """        keep = scores.new(scores.size(0)).zero_().long()      if boxes.numel() == 0:          return keep      x1 = boxes[:, 0]      y1 = boxes[:, 1]      x2 = boxes[:, 2]      y2 = boxes[:, 3]      area = torch.mul(x2 - x1, y2 - y1)      v, idx = scores.sort(0)  # sort in ascending order      # I = I[v >= 0.01]      idx = idx[-top_k:]  # indices of the top-k largest vals      xx1 = boxes.new()      yy1 = boxes.new()      xx2 = boxes.new()      yy2 = boxes.new()      w = boxes.new()      h = boxes.new()        # keep = torch.Tensor()      count = 0      while idx.numel() > 0:          i = idx[-1]  # index of current largest val          # keep.append(i)          keep[count] = i          count += 1          if idx.size(0) == 1:              break          idx = idx[:-1]  # remove kept element from view          # load bboxes of next highest vals          torch.index_select(x1, 0, idx, out=xx1)          torch.index_select(y1, 0, idx, out=yy1)          torch.index_select(x2, 0, idx, out=xx2)          torch.index_select(y2, 0, idx, out=yy2)          # store element-wise max with next highest score          xx1 = torch.clamp(xx1, min=x1[i])          yy1 = torch.clamp(yy1, min=y1[i])          xx2 = torch.clamp(xx2, max=x2[i])          yy2 = torch.clamp(yy2, max=y2[i])          w.resize_as_(xx2)          h.resize_as_(yy2)          w = xx2 - xx1          h = yy2 - yy1          # check sizes of xx1 and xx2.. after each iteration          w = torch.clamp(w, min=0.0)          h = torch.clamp(h, min=0.0)          inter = w*h          # IoU = i / (area(a) + area(b) - i)          rem_areas = torch.index_select(area, 0, idx)  # load remaining areas)          union = (rem_areas - inter) + area[i]          IoU = inter/union  # store result in iou          # keep only elements with an IoU <= overlap          idx = idx[IoU.le(overlap)]      return keep, count

以上就是有關ssd網路結構以及每一層的輸出的含義.這些已經足夠我們了解推理過程了.即給定一個圖,模型如何預測出box的位置.後面我們將繼續關注訓練的過程.

loss計算

第一個要解決的問題就是box匹配的問題.即每一次訓練,怎樣的預測框算是預測對了?我們需要計算這些模型認為的預測對了的box和真正的ground truth box之間的差異.

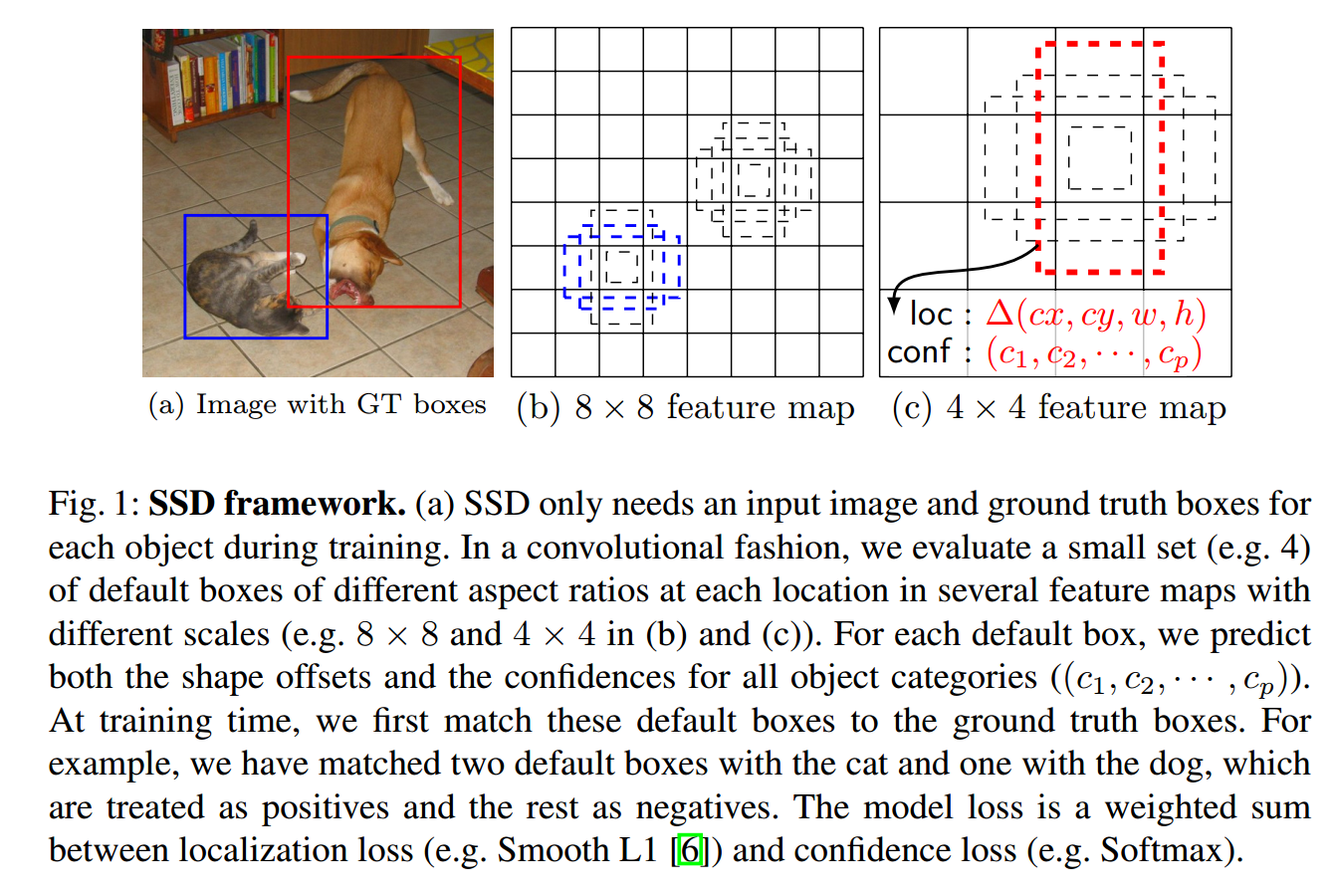
如上所示,貓的ground truth box匹配了2個default box,狗的ground truth box匹配了1個default box.

匹配策略

匹配策略是

• 把gt box朝著prior box做匹配,和gt box的IOU最高的prior box被選為正樣本
• 任意和gt box的IOU大於0.5的也被選為正樣本
  有一個問題困擾了我好久，第二步不是包含第一步嗎,直到某天豁然開朗，可能所有的prior box與gt box的iou都<閾值，第一步就是為了保證至少有一個prior box與gt box對應

box_utils.py

def match(threshold, truths, priors, variances, labels, loc_t, conf_t, idx):      # jaccard index     #[objects_num,priorbox_num]      overlaps = jaccard(          truths,          point_form(priors)      )      # (Bipartite Matching)      # [num_objects,1] best prior for each ground truth      best_prior_overlap, best_prior_idx = overlaps.max(1, keepdim=True) #返回每行的最大值,即哪個priorbox與當前obj gt box的IOU最大      # [1,num_priors] best ground truth for each prior      best_truth_overlap, best_truth_idx = overlaps.max(0, keepdim=True) #返回每列的最大值,即哪個obj gt box與當前prior box的IOU最大      best_truth_idx.squeeze_(0) #best_truth_idx的shape是[1,num_priors],去掉第0維度將shape變為[num_priors]      best_truth_overlap.squeeze_(0) #同上      best_prior_idx.squeeze_(1) #best_prior_idx的shape是[num_objects,1],去掉第一維度變為[num_objects]      best_prior_overlap.squeeze_(1)      best_truth_overlap.index_fill_(0, best_prior_idx, 2)  # ensure best prior #把best_truth_overlap第0維度best_prior_idx位置的值的替換為2,以使其肯定>theshold      # TODO refactor: index  best_prior_idx with long tensor      # ensure every gt matches with its prior of max overlap      for j in range(best_prior_idx.size(0)):          best_truth_idx[best_prior_idx[j]] = j      matches = truths[best_truth_idx]          # Shape: [num_priors,4]      conf = labels[best_truth_idx] + 1         # Shape: [num_priors]      conf[best_truth_overlap < threshold] = 0  # label as background      loc = encode(matches, priors, variances)      loc_t[idx] = loc    # [num_priors,4] encoded offsets to learn      conf_t[idx] = conf  # [num_priors] top class label for each prior 

這裡的邏輯實際上是有點繞的.給個具體的例子會更好滴幫助你理解.
我們假設一張圖片里有2個object.那就有2個gt box,假設計算出3個(實際是8732個)prior box.計算每個gt box和每個prior box的iou即得到一個兩行三列的overlaps.

import torch  #假設一幅圖裡有2個obj,預測出3個box,其iou如overlaps所示  truths = torch.Tensor([[1,2,3,4],[5,6,7,8]]) #2個gtbox 每個box坐標由四個值確定  labels = torch.Tensor([[5],[6]])#2個obj分別屬於類別5,類別6  overlaps = torch.Tensor([[0.1,0.4,0.3],[0.5,0.2,0.6]])  #overlaps = torch.Tensor([[0.9,0.9,0.9],[0.8,0.8,0.8]])    best_prior_overlap, best_prior_idx = overlaps.max(1, keepdim=True) #[2,1]  #print(best_prior_overlap)  #print(best_prior_idx) #與目標gt box iou最大的prior box 下標    best_truth_overlap, best_truth_idx = overlaps.max(0, keepdim=True) #返回每列的最大值,即哪個obj gt box與當前prior box的IOU最大  #print(best_truth_overlap) #[1,3]  #print(best_truth_idx) #與prior box iou最大的gt box 下標    best_truth_idx.squeeze_(0) #best_truth_idx的shape是[1,num_priors],去掉第0維度將shape變為[num_priors]  best_truth_overlap.squeeze_(0) #同上    best_prior_idx.squeeze_(1) #best_prior_idx的shape是[num_objects,1],去掉第一維度變為[num_objects]  best_prior_overlap.squeeze_(1)    print(best_prior_idx)  print(best_truth_idx)    #把和gt box的iou最大的prior box的iou設置為2(只要大於閾值就可以了),以確保這個prior box一定會被保留下來.  best_truth_overlap.index_fill_(0, best_prior_idx, 2)    #比如所有的prior box都和gt box1的iou=0.9,prior box2和gt box2的iou=0.8.  我們要確保prior box2被匹配到gt box2而不是gt box1.  #把overlaps = torch.Tensor([[0.9,0.9,0.9],[0.8,0.8,0.8]])試試就知道了  for j in range(best_prior_idx.size(0)):      print(j)      best_truth_idx[best_prior_idx[j]] = j    print(best_truth_idx)    matches = truths[best_truth_idx]  #[3,4] 列代表每一個對應的gt box的坐標  print(matches)    print(best_truth_overlap)    conf = labels[best_truth_idx] + 1 #[3,1]每一列代表當前prior box對應的gt box的類別  print(conf.shape)  #conf[best_truth_overlap < threshold] = 0  #過濾掉iou太低的,標記為background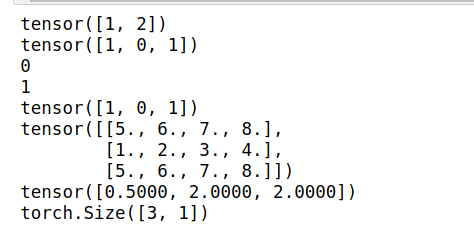

至此,我們得到了matches,即對每一個prior box都找到了其對應的gt box.也得到了conf.即prior box歸屬的類別.如果iou過低的,類別就被標記為background.

接下來

def encode(matched, priors, variances):      # dist b/t match center and prior's center      g_cxcy = (matched[:, :2] + matched[:, 2:])/2 - priors[:, :2]      # encode variance      g_cxcy /= (variances[0] * priors[:, 2:])      # match wh / prior wh      g_wh = (matched[:, 2:] - matched[:, :2]) / priors[:, 2:]      g_wh = torch.log(g_wh) / variances[1]      # return target for smooth_l1_loss      return torch.cat([g_cxcy, g_wh], 1)  # [num_priors,4]  

我們比較prior box和其對應的gt box的差異.注意這裡的matched的格式是(lefttop_x,lefttop_y,rightbottom_x,rightbottom_y).
所以這裡得到的其實是gt box和prior box之間的偏移.

計算loss

對於所有的prior box而言,一共可以分為三種類型

• 正樣本
• loss排名靠前的xx個負樣本
• 其餘負樣本
  其中正樣本即:與ground truth box的iou超過閾值或者iou最大的prior box.
  負樣本:正樣本之外的prior box.

損失函數分為2部分,一部分是坐標偏移的損失,一部分是類別資訊的損失.

在計算loc損失的時候,只考慮正樣本. 在計算conf損失的時候,即考慮正樣本又考慮負樣本.並且保持負樣本:正樣本=3:1.

程式碼實現在:
multibox_loss.py

class MultiBoxLoss(nn.Module):      def forward(self, predictions, targets):        

偽程式碼可以表述為

#根據匹配策略得到每個prior box對應的gt box  #根據iou篩選出positive prior box  #計算conf loss  #篩選出loss靠前的xx個negative prior box.保證neg:pos=3:1  #計算交叉熵  #歸一化處理

• 坐標偏移的loss

        pos_idx = pos.unsqueeze(pos.dim()).expand_as(loc_data)          loc_p = loc_data[pos_idx].view(-1, 4)  #預測得到的偏移量          loc_t = loc_t[pos_idx].view(-1, 4)     #真實的偏移量          loss_l = F.smooth_l1_loss(loc_p, loc_t, size_average=False)  #我們回歸的就是相對default box的偏移

用smooth_l1_loss. 程式碼比較簡單,不多講了.

Hard negative mining
在匹配default box和gt box以後,必然是有大量的default box是沒有匹配上的.即只有少量正樣本,有大量負樣本.對每個default box,我們按照confidence loss從高到低排序.我們只取排在前列的一些default box去計算loss,使得負樣本:正樣本在3:1. 這樣可以使得模型更加快地優化,訓練更穩定.

關於目標檢測中的樣本不平衡可以參考https://zhuanlan.zhihu.com/p/60612064

簡單滴說就是,負樣本使得我們學到背景資訊,正樣本使得我們學到目標資訊.所以二者都需要,並且保持一個合適比例.論文里用的是3:1.
對應程式碼即MultiBoxLoss.negpos_ratio

        # Compute max conf across batch for hard negative mining          batch_conf = conf_data.view(-1, self.num_classes)  #[batch*8732,21]          loss_c = log_sum_exp(batch_conf) - batch_conf.gather(1, conf_t.view(-1, 1)) #conf_t的列方向是類別資訊            # Hard Negative Mining          loss_c[pos] = 0  # filter out pos boxes for now          loss_c = loss_c.view(num, -1)          _, loss_idx = loss_c.sort(1, descending=True)          _, idx_rank = loss_idx.sort(1)          num_pos = pos.long().sum(1, keepdim=True)          num_neg = torch.clamp(self.negpos_ratio*num_pos, max=pos.size(1)-1)          #得到負樣本的index          neg = idx_rank < num_neg.expand_as(idx_rank)

這時候的loss還不是網路的conf loss,並不是論文里的l_conf.

def log_sum_exp(x):      """Utility function for computing log_sum_exp while determining      This will be used to determine unaveraged confidence loss across      all examples in a batch.      Args:          x (Variable(tensor)): conf_preds from conf layers      """      x_max = x.data.max()      return torch.log(torch.sum(torch.exp(x-x_max), 1, keepdim=True)) + x_max

這裡用到了一個trick.參考https://github.com/amdegroot/ssd.pytorch/issues/203,https://stackoverflow.com/questions/42599498/numercially-stable-softmax
為了避免e的n次冪太大或者太小而無法計算,常常在計算softmax時使用這個trick.

這個函數嚴重影響了我對loss_c的理解,實際上,你可以把上述函數中的x_max移除.那這個函數
那麼loss_c就變為了

loss_c = torch.log(torch.sum(torch.exp(batch_conf), 1, keepdim=True)) - batch_conf.gather(1, conf_t.view(-1, 1))

就好理解多了.

conf_t的列方向是相應的label的index. batch_conf.gather(1, conf_t.view(-1, 1))得到一個[batch*8732,1]的tensor,即只保留prior box對應的label的概率預測資訊.

那總體的loss即為所有類別的loss之和減去這個prior box應該負責的label的loss.

得到loss_c以後,我們去得到正樣本/負樣本的index

        # 選出loss最大的一些負樣本 負樣本:正樣本=3:1          # Hard Negative Mining          loss_c = loss_c.view(num, -1) #[batch,8732]          loss_c[pos] = 0  # filter out pos boxes for now          _, loss_idx = loss_c.sort(1, descending=True)  #對每張圖的priorbox的conf loss逆序排序          print(_[0,:],loss_idx[0]) #[batch,8732] 每一列的值為prior box的index          _, idx_rank = loss_idx.sort(1)          print(_[0,:],idx_rank[0,:])  #[batch,8732] 每一列的值為prior box在loss_idx的位置.我們要選取前loss_idx中的前xx個.(xx=3倍負樣本)          num_pos = pos.long().sum(1, keepdim=True)          print(num_pos) #[batch,1] 列的值為每張圖的正樣本數量          #求得負樣本的數量,3倍正樣本,如果3倍正樣本>全部prior box,則設置負樣本數量為prior box數量          num_neg = torch.clamp(self.negpos_ratio*num_pos, max=pos.size(1)-1)          print(num_neg)          #選出loss排名最靠前的num_neg個負樣本          neg = idx_rank < num_neg.expand_as(idx_rank)          print(neg)  

至此,我們就得到了正負樣本的下標.接下來就可以計算預測值與真值的差異了.

        loss_c = F.cross_entropy(conf_p, targets_weighted, size_average=False)            # Sum of losses: L(x,c,l,g) = (Lconf(x, c) + αLloc(x,l,g)) / N            N = num_pos.data.sum()          loss_l /= N          loss_c /= N          return loss_l, loss_c  

用交叉熵衡量loss. 最後除以正樣本的數量,做歸一化處理.
https://pytorch.org/docs/stable/nn.html#torch.nn.CrossEntropyLoss

在計算loss前,不需要手動softmax轉換成概率值了.

訓練

前面已經實現了網路結構創建,loss計算.接下來就可以實現訓練了.
實現在train.py
精簡後的主要邏輯如下:

    ssd_net = build_ssd('train', cfg['min_dim'], cfg['num_classes'])      net = ssd_net        optimizer = optim.SGD(net.parameters(), lr=args.lr, momentum=args.momentum,                            weight_decay=args.weight_decay)      criterion = MultiBoxLoss(cfg['num_classes'], 0.5, True, 0, True, 3, 0.5,                               False, args.cuda)        for iteration in range(args.start_iter, cfg['max_iter']):          # load train data          images, targets = next(batch_iterator)            # forward          out = net(images)            # backprop          optimizer.zero_grad()          loss_l, loss_c = criterion(out, targets)          loss = loss_l + loss_c          loss.backward()          optimizer.step()      

即

• 定義網路結構
• 定義損失函數及反向傳播求梯度方法
• 載入訓練集
• 前向傳播得到預測值
• 計算loss
• 反向傳播,更新網路權重參數

涉及到的部分torch中函數用法參考:https://www.cnblogs.com/sdu20112013/p/11731741.html