狄利克雷卷積 & 莫比烏斯反演
積性函數與完全積性函數
積性函數
若一個數論函數\(f\)滿足當\(gcd(n,m)=1\)時,\(f(nm)=f(n)f(m)\)
則稱\(f\)為積性函數
一些常見的積性函數
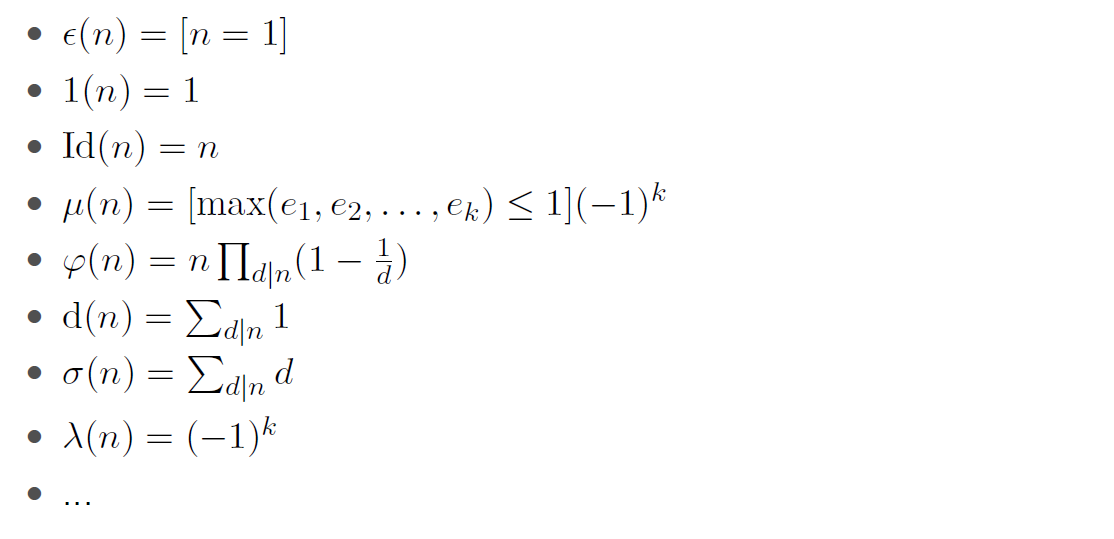
完全積性函數
若一個積性函數函數\(f\)滿足當\(gcd(n,m)\ne1\)時,也有\(f(nm)=f(n)f(m)\)
則稱\(f\)為完全積性函數
狄利克雷卷積
定義兩個數論函數的狄利克雷卷積\(*\)
若\(t=f*g\)
\[t(n)=\sum\limits_{i|n}f(i)g(\frac{n}{i})
\]
\]
等價於
\[t(n)=\sum\limits_{ij=n}f(i)g(j)
\]
\]
狄利克雷卷積有以下性質(兩個數論函數相等,是指兩個函數的每一項都相等):
- 交換律 \(f*g=g*f\)
- 結合律 \(f*(g*h)=(f*g)*h\)
- 分配律 \(f*h+g*h=(f+g)*h\)
- 沒有名字\((xf)*g=x(f*g)\)
- 單位元\(\epsilon*f=f\) ,其中\(\epsilon(n)=[n==1]\)
- 逆元:對於每一個\(f(1)≠0\)的函數\(f\),都有\(f∗g=ϵ\)
討論一下第六個結論,如何求一個函數的逆呢?
只需要定義
\[g(n)=\frac{1}{f(1)}\left([n==1]-\sum\limits_{i|n,i\ne1}f(i)g(\frac{n}{i})\right)
\]
\]
這樣的話
\[\sum\limits_{i|n}f(i)g(\frac{n}{i})=f(1)g(n)+\sum\limits_{i|n,i\ne1}f(i)g(\frac{n}{i})=[n==1]
\]
\]
幾種比較常見的卷積關係:
\(\mu*1=\epsilon\) 【莫比烏斯反演】【\(\mu\)與\(1\)互為逆元】
\(\varphi*1=Id\)
\(\varphi=Id*\mu\)
\(d=1*1\)
\(1=\mu*d\)
莫比烏斯反演
我們定義\(1\)的逆是\(\mu\)
這樣的話,如果\(g=f∗1\),就有\(f=f∗1∗\mu=g∗\mu\)
換句話說,就是
\[g(n)=\sum\limits_{d|n}f(d)\Leftrightarrow f(n)=\sum\limits_{d|n}\mu(\frac{n}{d})g(d)
\]
\]
也可以這樣子
\[g(d)=\sum\limits_{d|n}f(n)\Leftrightarrow f(d)=\sum\limits_{d|n}\mu(\frac{n}{d})*g(n)
\]
\]


