EM演算法和GMM演算法的相關推導及原理
極大似然估計
我們先從極大似然估計說起,來考慮這樣的一個問題,在給定的一組樣本x1,x2······xn中,已知它們來自於高斯分布N(u, σ),那麼我們來試試估計參數u,σ。
首先,對於參數估計的方法主要有矩估計和極大似然估計,我們採用極大似然估計,高斯分布的概率密度函數如下:
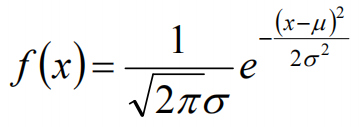
我們可以將x1,x2,······,xn帶入上述式子,得:
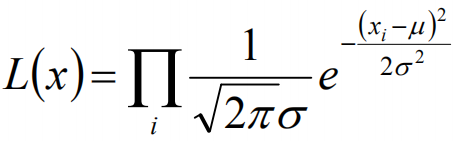
接下來,我們對L(x)兩邊去對數,得到:
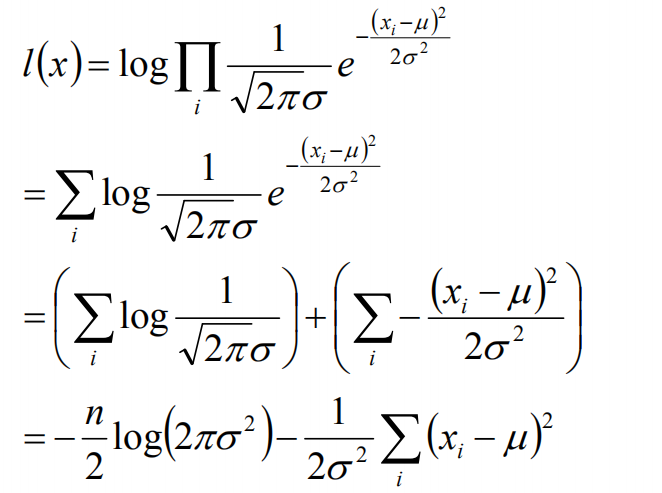
於是,我們得到了l(x)的表達式,下面需要對其計算極大值:
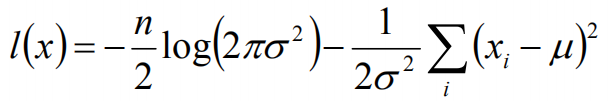
通過對目標函數的參數u,σ分別求偏導,很容易得到:

對於上述的結果,和矩估計是一樣,它的含義就是:樣本的均值即為高斯分布的均值,樣本的方差即為高斯分布的方差。
通過上面的問題分析,我們來看這樣的一個問題,假設在班級中隨機挑選100名同學,並且測量了這100名同學的身高,如果這100個樣本服從的是正態分布,那麼我們可以用樣本的均值和方差等於正態分布的均值和方差來估計參數u和σ。但是樣本中存在男同學和女同學,它們分別服從N1(u1, σ1)和N2(u2, σ2)的分布,那麼我們應該如何估計u1, σ1,u2, σ2參數呢?
我們可以通過假設隨機變數x是有k個高斯分布混合而成,取各個高斯分布的概率的φ1,φ2,······φk,第i個高斯分布的均值為ui,方差為∑i。那麼,我們可以建立如下目標函數:
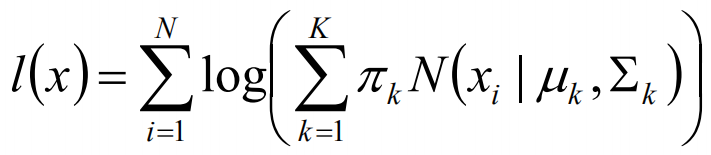
上述的式子中,由於在對數函數中存在加和,無法直接求導計算極大值,我們可以將其分成兩步:
第一步:估算數據來自哪個組份
估計數據是有哪個組份生成的概率,對於數據xi來說,它是由第k個組份生成的概率為:
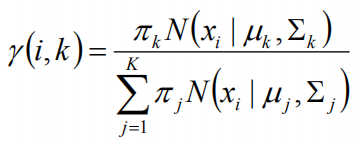
在上面的式子中,u和∑是需要進行估計的,這裡採用迭代法,在計算r(i,k)的時候,假定u和∑均為已知的,但是在第一次計算時,我們根據先驗知識給定u和∑。
第二步:估計每個組份的參數
假設上一步中得到的r(i,k)就是正確的數據xi由組份k生成的概率,亦可以當做該組份在生成這個數據上所做的貢獻,或者也可以看做xi其中r(i,k)*xi部分是由組份k所生成的。對於所有的數據點,現在司機上可以看作組份k生成了{γ(i,k)*xi|i=1,2,…N}這些點。組份k是一個標準的高斯分布,利用上面的結論:
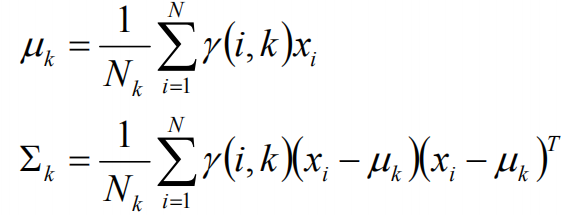
EM演算法的提出
假定有訓練集{x1, x2,····xm},包含m個獨立樣本,要求從中找到該組數據的模型p(x, z)的參數。通過構建極大似然估計建立目標函數:
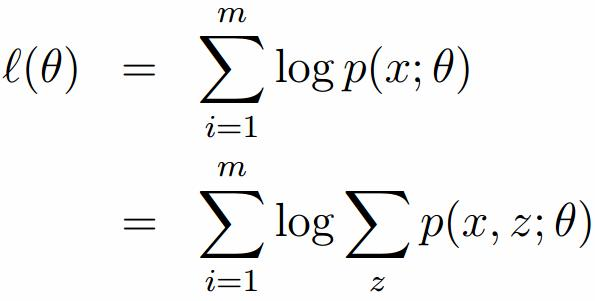
在上面的式子中,z是隱隨機變數,直接找到參數的估計是很困難的。這裡我們採用建立目標函數的下界,並且求該下界的最大值,不斷的重複這個過程,直到收斂到局部的最大值。
Jensen不等式
令Qi是z的某一個分布,並且Qi>=0,有:
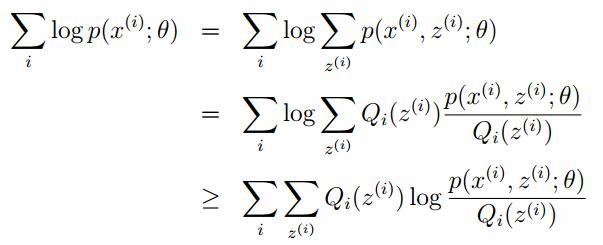
我們需要尋找盡量緊的下界,為了使得等式成立:
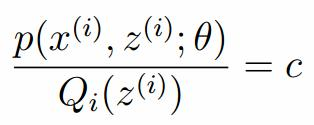
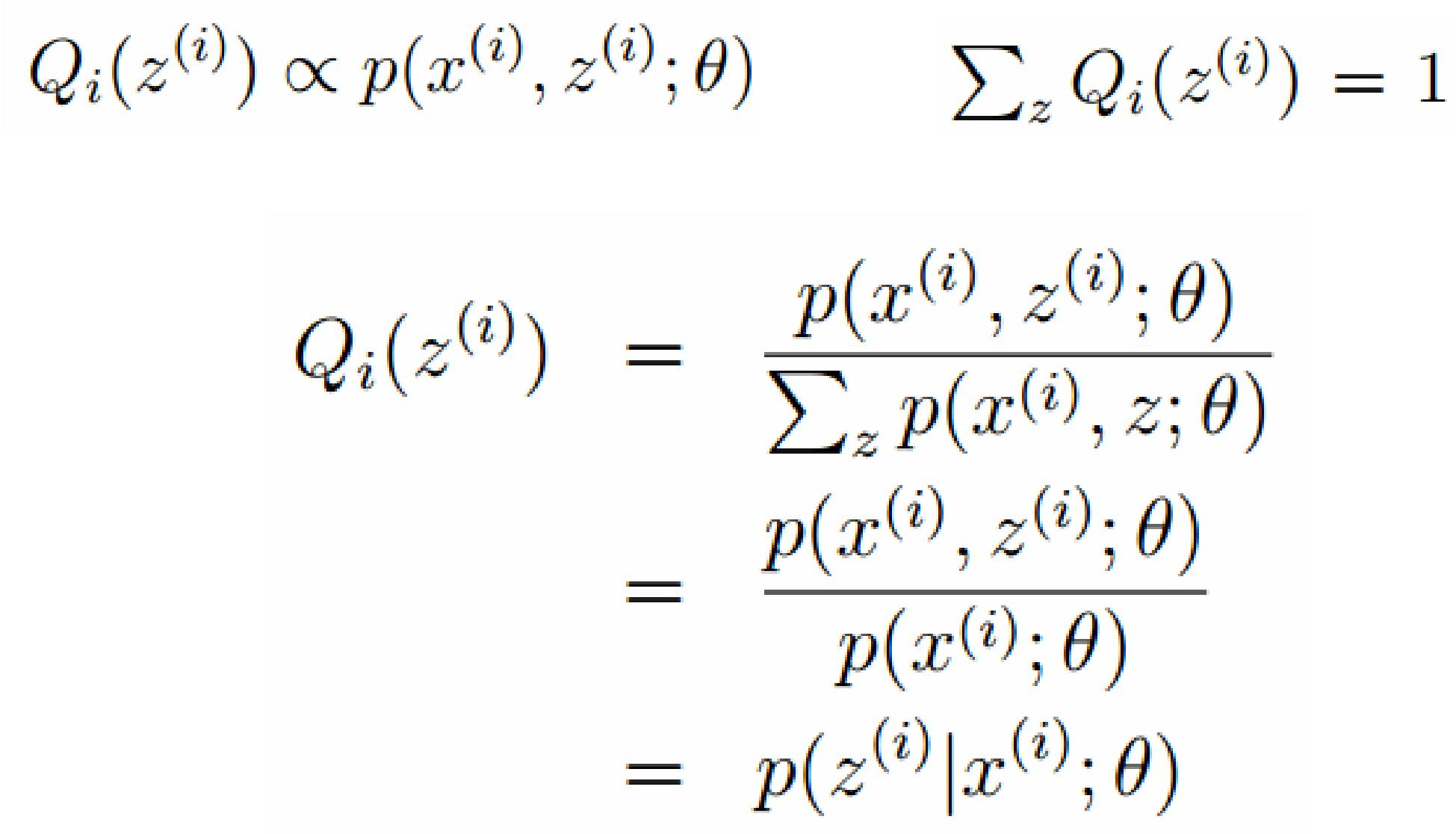
EM演算法的整體框架
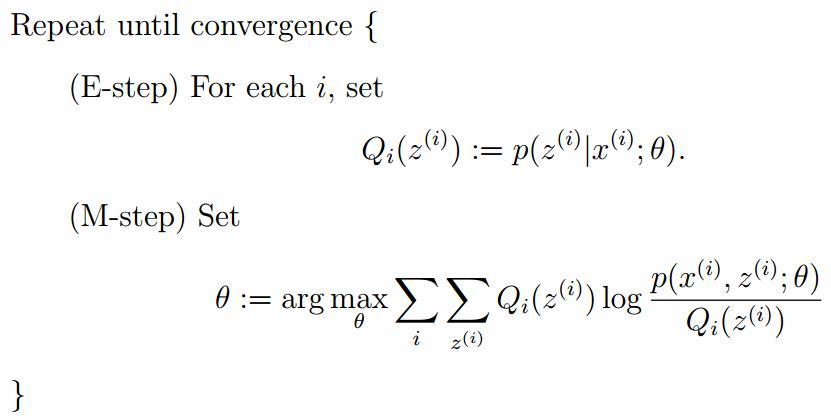
E-step
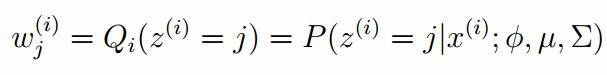
M-step
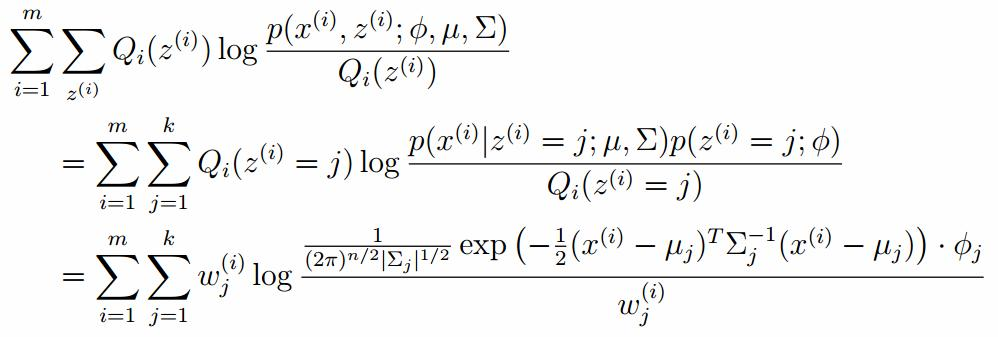
對上面的公式求偏導

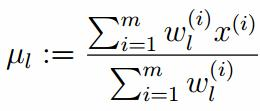
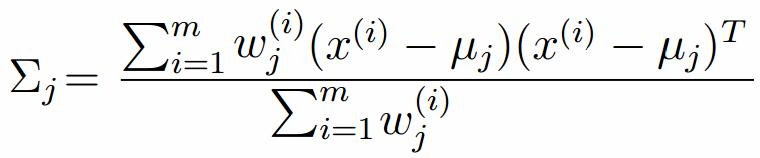
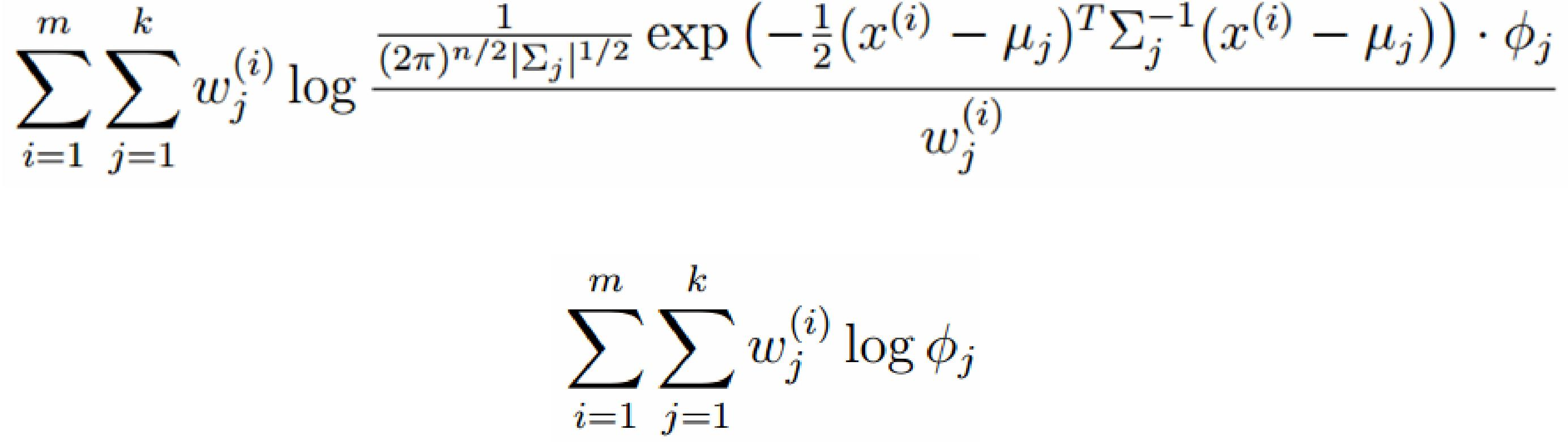
由於多項分布的概率和為1,建立拉個朗日方程:
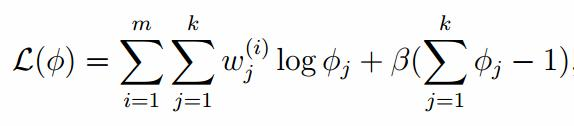
計算偏導: