CodeTON Round 3 (C.差分維護，D.容斥原理)

2022 年 11 月 7 日
筆記
菜雞的算法路

C. Complementary XOR

題目大意：

給你兩個01串ab，問你是否可以通過一下兩種操作在不超過n+5次的前提下將兩個串都變為0，同時需要輸出可以的操作方案

選擇一個區間[l,r]
將串a的[l,r]翻轉(0 $\rightarrow$ 1,1 $\rightarrow$0)，同時將b的[1,l)和（r,n]區間翻轉

解題思路：

通過寫兩組樣例，我們可以嘗試這種思路，因為我們需要輸出可以的操作方案，我們很難去考慮同時操作a,b兩個串的操作，所以我們嘗試只考慮a串。將a串的全部0變成1，觀察b串經過這種操作後的結果。
我們可以發現，如果a串全為1，那b串此時有三種可能：

全為0
全為1
即含1，又含0

我們發現狀況1可以通過對a進行一次[1,n]操作使a，b都為0
狀況2可以通過對a進行一次[1,1],[2,n]操作使a,b都為0（觀察最後一個樣例）
但是狀況3我們沒有任何辦法使得a，b都為0

自此整個題目分析完畢，我們只需要記錄讓a全部為1的操作對b的影響，最後看b串是否屬於情況1,2即可

我們觀察操作對b的影響是對[1,l)和（r,n]整個的影響，所以可以理解為對[1,l)和（r,n]操作次數都+1，因為翻轉2次等於沒翻轉，（只有翻轉奇數次才會真的翻轉），因為是對整個區間+1，所以就可以考慮用差分維護（O(1)）

操作影響如下，假如選擇的區間為[i,i],對b的影響就是b[1] += 1;b[i]-=1;b[i+1] += 1;

代碼實現：

# include<iostream>
# include<bits/stdc++.h>
using namespace std;
# define int long long
# define endl "\n"
const int N = 2e5 + 10, inf = 1e9 + 7;
int b[N];
int a[N];
void solve() {
	int n;
	cin>>n;
	for(int i = 1;i <= n+1;++i) b[i] = a[i] = 0;
	string s1,s2;
	cin>>s1>>s2;
	s1 = "?"+s1;
	s2 = "?"+s2;
	bool ok = true;
	vector<pair<int,int>> ans;
	for(int i = 1;i <= n;++i)//看看兩個串是不是本身就為全0
        {
		if(s1[i]!= '0'||s2[i] != '0') {
			ok = false;
			break;
		}
	}
	if(ok){
		cout<<"YES"<<endl;
		cout<<0<<endl;
		return;
	}
	for(int i = 1;i <= n;++i){
		if(s1[i] == '0'){
			ans.push_back({i,i});
			b[1] += 1;//差分維護對b的影響
			b[i]-=1;
			b[i+1] += 1;
		}
	}
	for(int i = 1;i <= n;++i){
		a[i] = a[i-1]+b[i];//前綴和計算對每個位置的影響
	}
	for(int i = 1;i <= n;++i){
		if(a[i]&1){//如果操作次數為奇數則進行變化
			if(s2[i] == '0') s2[i] = '1';
			else s2[i] = '0';
		}
	}
	for(int i = 1;i <= n;++i){
		if(s2[i] != s2[1])//非（全0或者全1）
                {
			cout<<"NO"<<endl;
			return;
		}
	}
	if(s2[1] == '0'){
		ans.push_back({1,n});
	}
	else{
		ans.push_back({1,1});
		ans.push_back({2,n});
	}
	cout<<"YES"<<endl;
	cout<<ans.size()<<endl;
	for(auto [x,y]:ans){
		cout<<x<<" "<<y<<endl;
	}
	
	
	
}
int tt;
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	tt = 1;
	cin >> tt;
	while (tt--)solve();


	return 0;
}

D. Count GCD

題目大意：

對於給定n,m，給你一個含n個數的數組，數組中每個數的取值範圍在[1,m]

問能構造多少組數組b滿足一下條件：

b[i] $\in$[1,m]
gcd(b[1],b[2],…,b[i]) = a[i]

解題思路：

基本看到構造多少組b滿足以上條件的就可以考慮原數組每一位的貢獻了，類似於組合數學是每一位的貢獻的積為總的組數
所以總的框架就是

        int ans = 1;
	for(int i = 2;i <= n;++i){
		if(a[i] == a[i-1]){
                        int t = m/a[i];//當前這一位的貢獻
			ans = ans*t%mod;//總貢獻
		}
		else{
			int t = cal(a[i-1]/a[i],m/a[i]);//當前這一位的貢獻
			ans = ans*t%mod;
		}
	}
	cout<<ans<<endl;

然後考慮每一位的貢獻是怎麼樣的形式
我們寫兩組數據大概可以的到一下的思路：
因為是前綴gcd，所以明顯每個數的質因子是不斷變小的，然後我們如果要求解b[i]
就有如下思路：gcd(a[i-1],b[i]) = a[i]
那我們要求的其實就是a[i]的倍數，比如a[i-1] = 6,a[i] = 3,那能夠滿足g(6,b[i]) = 3的只有3的倍數（3,6,9,12,15…..k*3<= m）,但是我們很容易就發現6,12是不能選的gcd(6,6||12) = 6，同理如果m/a[i] (所有的倍數)包含a[i-1]/a[i]的質因子的時候就都不能選

所以，問題可以轉化為：從[1，m/a[i]]中選與（a[i-1]/a[i])互質的數有多少個

於是引入容斥原理：

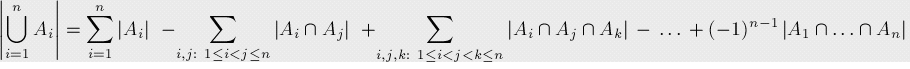
Tot = C$_n$$^1$ – C$_n$$^2$ + C$_n$$^3$…..

用韋恩圖表示如下：

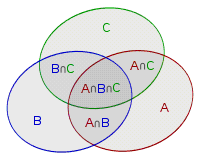
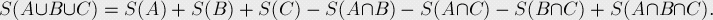
所以我們就考慮用總的（m/a[i])-res（所有與a[i-1]/a[i]不互質的數的並集）

之所以取與a[i-1]/a[i]不互質的數的並集是因為它比較好表示，用（m/a[i])/（選中的因子的積)就是不互質數的數量
比如從1,2,3,4,5,6中求與2,3不互質的數
實際上就是6-（2的倍數（{2,4,6} $\rightarrow$6/2 = 3）+3的倍數（{3,6} $\rightarrow$6/3 = 2）-（2*3）的倍數（{6} $\rightarrow$6/6 = 1）） = 6-3-2+1 = 2{1,5}

代碼實現：

# include<iostream>
# include<bits/stdc++.h>
using namespace std;
# define int long long
# define endl "\n"
const int N = 2e5 + 10, mod = 998244353;
int a[N];
//在[1,top]範圍內，找和n互質的數的個數 
int cal(int n,int top){
	vector<pair<int,int>> divisors;//質因子
	for(int i = 2;i*i<=n;++i){
		if(n%i == 0){
			int s  = 0;
			while(n%i == 0) n/=i,s++;
			divisors.push_back({i,s});//i的s次 
		} 
	} 
	if(n>1) divisors.push_back({n,1});
	
	int res = 0,m = divisors.size();
	for(int i = 1;i< (1<<m);++i)//二進制模擬第j個元素選還是不選
      {
		int t = 1,s = 0;
		for(int j = 0;j < m;++j){
			if(i>>j&1){
				if(t*divisors[j].first>top){
					t = -1;
					break;
				}
				t *= divisors[j].first;
				s++;
			}
		}
		if(t != -1)
                {
			if(s%2) res += top/t;//如果選了奇數個元素就是加
			else res -= top/t;//偶數個元素是減
                                          //從容斥原理可以得到
		}
	}
	return top-res;
}

void solve() {
	int n,m;
	cin>>n>>m;
	for(int i = 1;i <= n;++i) cin>>a[i];
	for(int i = 2;i <= n;++i){
		if(a[i-1]%a[i]){
			cout<<0<<endl;
			return;
		}
	}
	int ans = 1;
	for(int i = 2;i <= n;++i){
		if(a[i] == a[i-1]){
			ans = ans*(m/a[i])%mod;
		}
		else{
			int t = cal(a[i-1]/a[i],m/a[i]);
			ans = ans*t%mod;
		}
	}
	cout<<ans<<endl;
	
}
int tt;
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	tt = 1;
	cin >> tt;
	while (tt--)solve();


	return 0;
}

Tags: 菜雞的算法路