機器學習:支持向量機(SVM)
SVM,稱為支持向量機,曾經一度是應用最廣泛的模型,它有很好的數學基礎和理論基礎,但是它的數學基礎卻比以前講過的那些學習模型複雜很多,我一直認為它是最難推導,比神經網絡的BP算法還要難懂,要想完全懂這個算法,要有很深的數學基礎和優化理論,本文也只是大概討論一下。本文中所有的代碼都在我的github。
硬間隔SVM推導
如果現在我們需要對一堆數據進行二分類處理,並且這些數據都是線性可分的(一條直線就能將數據區分開),那麼你會如何對之進行劃分?如圖1。
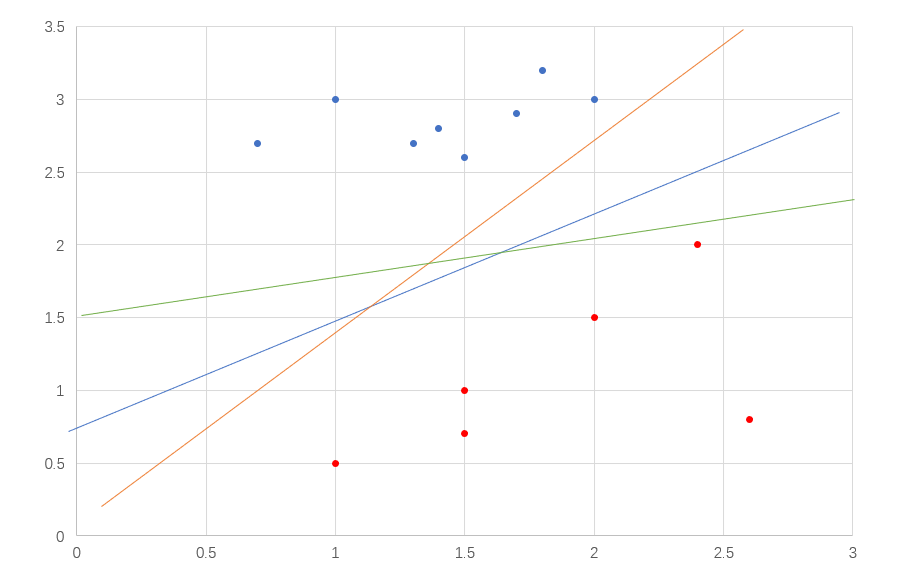
我們只需要在倆類數據的中間找出一條直線即可,如果數據是三維的,那麼我們需要找出中間的切分面,能將倆類數據劃分開的直線有很多,在圖1中就有三條,那麼你如何判斷哪一條才是最適合的呢?直觀來看,肯定是中間的藍色線,因為黃線太靠近藍點,綠線太靠近紅色,這樣的線對樣本擾動的容忍性低,在測試集中很容易就會出錯,而藍色線是受影響最小的,因為它距離倆類樣本最遠,這樣才具有泛化能力,那麼我們需要找出的線就是距離倆類樣本最遠,其實就是最中間的線,從圖1中可以看出平面上有很多點,問題在於哪些點才能衡量出線到倆類數據的距離呢?那肯定是距離線最近的那些點,我們把最近樣本點到劃分邊界的距離稱為間隔。我們的目標就是達到最大間隔的那個劃分邊界。下面先來求間隔。
間隔
用\(W^TX + b = 0\)來表示劃分邊界,我們先計算點到這個劃分邊界的距離,因為數據可能是高維的,所以不能用點到直線的距離,應該計算點到面的距離。圖2就是計算其中有一個\(P\)到面的距離。
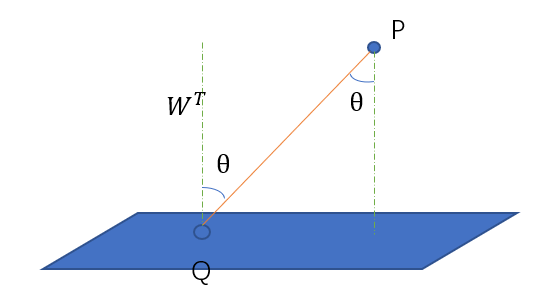
$Q$是平面上任意一點,其中$W^T$是平面的法向量,這個我們推導出來,假設平面上任意倆點$x_1,x_2$,
$$
W^T(x_1 – x_2) = W^Tx_1 – W^Tx_2 = (-b) – (-b) = 0
$$
因此$W^T$與平面垂直。設$P$到平面上距離為$d$,從圖中我們可以很容易的看出,
$$
\begin{align}
d & = |PQ|cos\theta \notag \\
& = |P – Q|cos
& = |P – Q| \frac{|W^T(P-Q)|}{|W||P – Q|} \notag \\
& = \frac{1}{|W|}|W^TP – W^TQ| \notag \\
\end{align}
$$
因為$Q$是平面上任意一點,所以$W^TQ + b = 0$,點$P$到平面上的距離公式變成
$$
d = \frac{1}{|W|}|W^TP + b|
$$
假設數據集\(D = \{(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\}\),點到劃分邊界的距離就是\(d = \frac{1}{|W|}|W^Tx_i + b|\),之前我們說最近樣本點到劃分邊界的距離稱為間隔,那麼間隔用公式表示就是
\]
這個公式也被稱為幾何間隔,是我們的目標。
因為\(\frac{1}{|W|}\)和\(min\)沒有關係,可以直接提到前面去,
\]
現在單獨來看這個公式,我們可以將絕對值符號替換掉不?絕對值裏面的數一定是正數,如果所有的數據都會正確分類,沒有那種錯誤的數據,那麼\(W^Tx_i + b\)在負類中的結果是負數,\(W^Tx_i + b\)在正類中的結果是正數,我們一般將負類表示為-1,正類表示為1,那麼就有辦法了,直接將之乘以各自的類別,
\]
我們再來看看這個式子的含義,數據如果帶入\(y_i(W^Tx_i + b)\),計算出來的肯定不是0,因為結果0代表這個點就在這個劃分邊界上,肯定是一個數,並且帶入的點離劃分邊界越遠,計算出來的結果就越大,我們就有更大的把握將之分類正確,那麼\(y_i(W^Tx_i + b)\)其實就是數據分類的置信度,我們也將之稱為函數間隔,這裡的置信度不是概率而是一個確切的值,沒有統一的量綱,會出現問題,我們如果將劃分邊界的\(W\)和\(b\)等比例放縮,比如將\(x + y + z + 1 = 0\)變成\(2x + 2y + 2z + 2 = 0\),這樣放縮過後的平面與原來的平面其實還是同一個平面,平面沒變,點的位置也沒變,那麼幾何間隔不變,但是函數間隔就發生了變化,擴大2倍,那麼我們就需要將劃分邊界的\(W\)和\(b\)的比例定下來,這個比例就是隨便定哪種,因為它不影響幾何間隔的大小,既然比例可以隨便定了,那麼我就定成最小點到平面距離為1的比例,也就是\(y_i(W^Tx_i + b) = 1\),那麼間隔大小就是
\]
我們的目標就是達到最大間隔的那個劃分邊界,別忘了還有條件,數據能夠被完全正確劃分,用公式表示就是,
s.t. y_i(W^Tx_i + b) \geq 1
\]
對於函數間隔設置為1,除了之前的代數角度,還可以從另一個角度來看,平面的變化就是\(W\)和\(b\)的變化,我們需要找出最好的劃分邊界,那麼就需要不斷地變化\(W\)和\(b\)來表示不同的劃分邊界,\(W\)和\(b\)有倆種,一種是等比例,另一種是不等比例,等比例變化之後還是原來的平面,這明顯不是我們想要的,我們想要的是不同的平面,那麼就需要不等比例,那麼我們就將函數間隔縮放成1,每次調整參數的時候,都會按比例把函數間隔縮放成1,這樣變化\(W\)和\(b\)就不會出現第一種情況了。
現在這個問題就變成了求最大值的問題,在機器學習中就是優化問題,在優化最值問題中,一般都求最小值,因為如果你求最大值的話,你沒有上界,你無法判斷出結果如何,但是在求最小值中,我們可以將0當成下界,所以可以將之轉化為最小值問題,就變成了\(\min\limits_{W,b}|W|\)。這裡就需要比較向量的大小,專業化就是度量向量大小,在數學中可以使用範式,最常用的歐氏距離就是2範式,我們也將之變成2範式,並且為了簡化之後的計算,在前面加上\(\frac{1}{2}\),就變成了
s.t. y_i(W^Tx_i + b) \geq 1,i=1,2,\dots,n
\]
我們可以利用QP解法來直接求這個最小值,但是一旦要引入核函數,那麼這種解法就很複雜了,沒有效率,因此需要利用優化來求解。
對偶
上面的求最值問題在機器學習中被稱為優化問題,從導數的時候,我們就學過求函數的最值,是利用導數為0,不過那時候是沒有約束條件的,後來上大學,高數中出現求等式約束條件下多元函數的極值,這個時候我們來看怎麼求,有了約束條件,那麼取值就有範圍,只能在這個等式中的值,我們可以通過圖來直觀的感受,這裡我們使用的是等高線圖來表示值的大小,並且用公式表示約束就是
s.t. h(x) = 0
\]
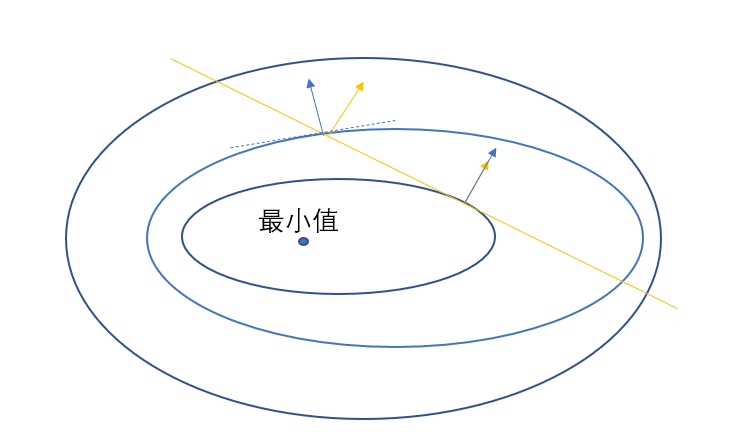
圖3中藍色線就是值的等高線,是函數$f(x)$的值,黃線就是等式約束條件,等式約束條件就是$h(x)$,在約束條件下,值是先變小,小到一定程度之後開始慢慢變大,當黃線到達極小值的時候,必然會有等高線與之相切,在極值點處$x^{\ast}$,黃線的梯度與等高線垂直,而等高線自身的梯度也是與等高線垂直,那麼黃線的梯度與等高線的梯度共線,自然就有了
$$
\bigtriangledown f(x^{\ast}) = \lambda \bigtriangledown h(x^{\ast})
$$
並且這個極值點處$x^{\ast}$在等式約束條件$h(x)$中也是存在的,因此也要滿足
$$
h(x^{\ast}) = 0
$$
上面倆個等式就是求極值點所需要的倆個條件,有了它們就能求,為了能將它們都包含在無約束的優化問題中,就設計出了這樣一個函數。
$$
L(x,\lambda) = f(x) + \lambda h(x) \\
s.t. \lambda \geq 0
$$
這個就是拉格朗日函數,一般拉格朗日函數都是需要對$x$和$\lambda$求偏導的,我們求出偏導就發現這倆個偏導和上面的倆個條件是一樣的。
$$
\frac{\partial L}{\partial x} = \bigtriangledown f(x) + \lambda \bigtriangledown h(x) = 0 \\
\frac{\partial L}{\partial \lambda} = h(x) = 0
$$
但是在實際優化問題中很多都是不等式約束,如果只有一個不等式的話,那麼還是使用拉格朗日即可。但是很多時候都有很多不等式,就比如我們上面的那個優化問題,它有\(n\)個不等式,這裡我們先看有倆個不等式約束條件的情況,
s.t. h_1(x) \leqslant 0,h_2(x) \leqslant 0
\]
我們可以畫出圖形,就是
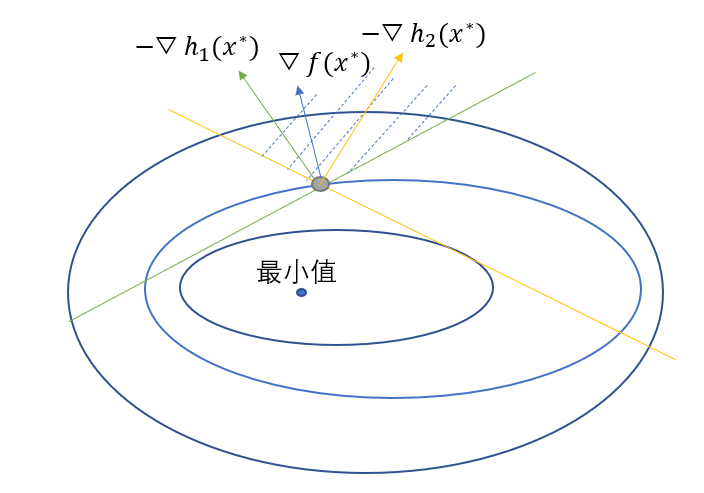
其中的黃線就是不等式約束$h_2(x)$,綠線就是$h_1(x)$,從圖中可以看到函數$f(x)$在極值點處的梯度始終在倆條不等式約束梯度的中間,這在向量空間就是表示$\bigtriangledown f(x^{\ast})$可以由$-\bigtriangledown h_1(x^{\ast})$和$-\bigtriangledown h_2(x^{\ast})$線性表示出來,並且線性表示的係數必定是非負的,公式可以表示
$$
\bigtriangledown f(x^{\ast}) = -\mu_1\bigtriangledown h_1(x^{\ast})-\mu_2\bigtriangledown h_2(x^{\ast}) \\
\mu_1 \geq 0, \mu_2 \geq 0
$$
這個倆個分別是梯度為0條件和可行條件,當然,在約束條件中,還有一種情況,就是線性表示與其中一些不等式梯度無關,比如再加上一個不等式約束為$h_3(x)$,在圖中表示就是
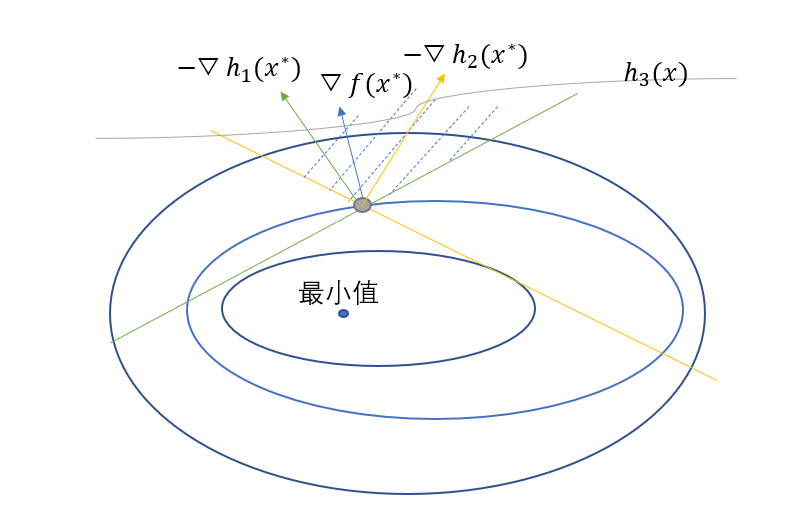
從圖中可以看出灰線所表示的約束與線性表示無關,因為它的最小值不在\(x^{\ast}\),但是我們的條件還是要寫成
\mu_1 \geq 0, \mu_2 \geq 0, \mu_3 \geq 0
\]
那麼其中的\(\mu_3\bigtriangledown h_3(x^{\ast})\)該如何消去呢,那麼再增加一個互補鬆弛條件就是
\]
因為在極值點處,\(h_1(x^{\ast})\)和\(h_2(x^{\ast})\)都是為0的,但是\(h_3(x^{\ast})\)不是0,用圖中線段的話,\(h_3(x^{\ast}) < 0\),那麼\(\mu_3 = 0\),這樣就能彌補上麵條件的缺陷了。這三個條件也被稱為KKT條件,KKT條件就是存在局部極小值點的必要條件,整理起來就是
\bigtriangledown f(x^{\ast}) + \mu_1\bigtriangledown h_1(x^{\ast})+\mu_2\bigtriangledown h_2(x^{\ast})+\mu_3\bigtriangledown h_3(x^{\ast}) =0 \\
\mu_1h_1(x^{\ast})+\mu_2h_2(x^{\ast})+\mu_3 h_3(x^{\ast}) = 0
\]
KKT條件是強對偶關係的充要條件,很多優化原問題很難求解,就需要找出原問題的對偶問題來求解。順便說一下,slater條件是強對偶關係的充分非必要條件。而凸二次規劃問題是一定滿足slater條件,我們的SVM就是一個凸二次規劃問題,因為它的目標函數\(f(x)\)是凸函數,並且約束都是放射函數,所以它一定是滿足強對偶關係的,但是下面推導我們依舊慢慢推導。
上面無論什麼約束,目標函數\(f(x)\)和約束函數\(h(x)\)都是變成一個式子的,因此我們先將之轉變為拉格朗日函數,變成無約束問題。將約束條件轉變為一般形式
\]
之後變成拉格朗日函數
s.t. \lambda_i \geq 0
\]
那麼我們能不能用拉格朗日函數來表示原問題呢?當然也是可以的,原問題是優化問題,可以轉變為極大極小問題,
\]
我們可以分情況來討論,當\(1-y_i(W^Tx_i + b) > 0\)的時候,\(L(x,\lambda)\)沒有最大值,或者說最大值是\(+\infty\),當\(1-y_i(W^Tx_i + b) \leq 0\)的時候,\(L(x,\lambda)\)有最大值,最大值就是\(\frac{1}{2}|W|^2\),那麼上面的極小極大可以變成
\]
其中\(\lambda_i\)用於表達約束,上式中\(\max\limits_{\lambda}L(x,\lambda)\)無法求,更無法使用偏導來求,因為式子\(L(x,\lambda)\)中的\(W\)和\(b\)沒有固定住。那麼這樣不行的話,就使用對偶問題來求,一般式都是滿足弱對偶關係的,也就是
\]
弱對偶關係很簡單,但是我們想要的是強對偶關係,那麼就需要用到上面所說的KKT條件,那麼我們求解KKT條件,先來看自帶的約束條件和KKT乘子條件就是
\lambda_i \geq 0
\]
第二個條件就是梯度為0條件,那麼需要對\(W\)和\(b\)進行求導
\frac{\partial L}{\partial b} = \sum\limits_{i=1}^{n}\lambda_iy_i = 0
\]
第三個條件就是互補鬆弛條件,對於任意的i,都有
\]
滿足了這三條要求,我們就可以轉化為對偶問題了,得到了
\]
那麼先對其中的\(W\)和\(b\)求偏導,其中也就是KKT中的第二個條件,
\frac{\partial L}{\partial b} = \sum\limits_{i=1}^{n}\lambda_iy_i = 0
\]
那麼可以得到
\sum\limits_{i=1}^{n}\lambda_iy_i = 0
\]
將之帶入到原方程中去,
L(x,\lambda) & = \frac{1}{2}W^TW + \sum\limits_{i=1}^{n}\lambda_i(1-y_i(W^Tx_i + b)) \notag \\
& = \frac{1}{2}\sum\limits_{i=1}^{n}\lambda_iy_ix_i^T\sum\limits_{j=1}^{n}\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i-\sum\limits_{i=1}^{n}\lambda_iy_iW^Tx_i -\sum\limits_{i=1}^{n}\lambda_iy_i b \notag \\
& = \frac{1}{2}\sum\limits_{i=1}^{n}\lambda_iy_ix_i^T\sum\limits_{j=1}^{n}\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i-\sum\limits_{i=1}^{n}\lambda_iy_i(\sum\limits_{j=1}^{n}\lambda_jy_jx_j^T)x_i -\sum\limits_{i=1}^{n}\lambda_iy_i b \notag \\
& = -\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i \notag \\
\end{align}
\]
那麼我們可以求得
\]
最終的式子就是
s.t. \lambda_i \geq 0,\sum\limits_{i=1}^{n}\lambda_iy_i = 0 \\
\]
劃分邊界中的\(W^{\ast} = \sum\limits_{i=1}^{n}\lambda_iy_ix_i\),而我們假設最近樣本點就是\((x_k,y_k)\),還可以求出\(b^{\ast} = y_k – \sum\limits_{i=1}^{n}\lambda_iy_ix_i^Tx_k\)。
超平面就是\(f(x) = sign(W^{T\ast}x+b^{\ast})\),還缺少的KKT條件就是
1-y_i(W^Tx_i + b) \leq 0 \\
\lambda_i(1-y_i(W^Tx_i + b)) = 0
\]
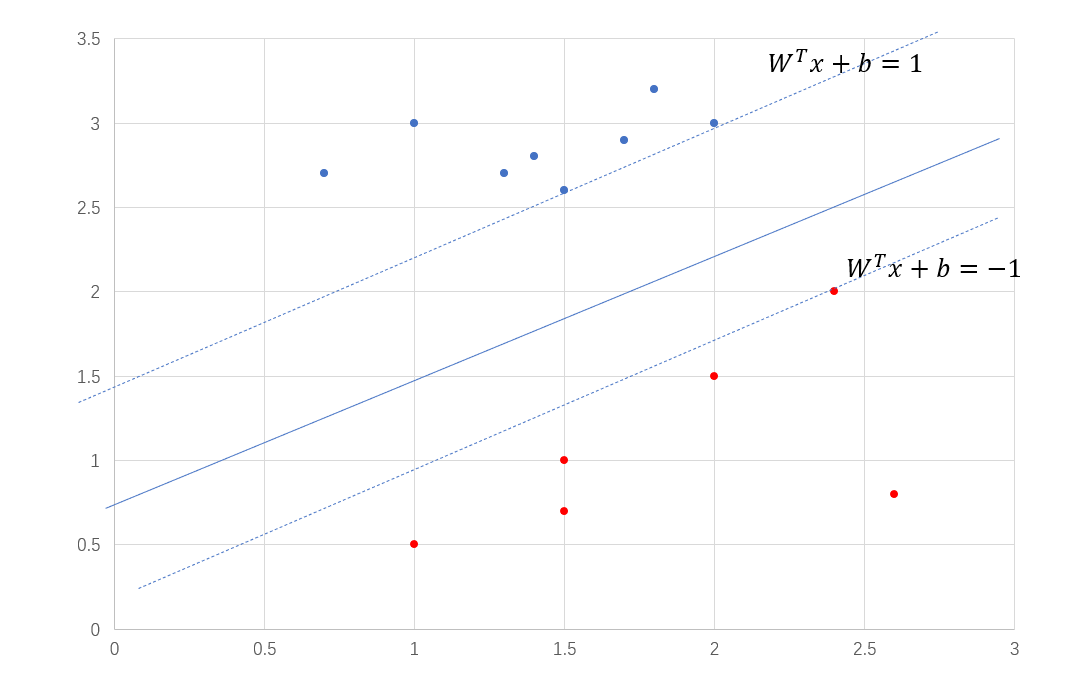
此時會過來看SVM,叫做支持向量機,其中的支持向量,其實就是最近樣本點,為什麼這樣說呢?我們看第四個條件,也就是\(\lambda_i(1-y_i(W^Tx_i + b)) = 0\),只有當\(y_i(W^Tx_i + b) = 1\)的時候,\(\lambda_i\)才不會為0,如果\(y_i(W^Tx_i + b) > 1\),那麼\(\lambda_i\)為0,\(\lambda_i\)為0的話就對超平面起不到任何的作用,你可以看\(W\)和\(b\)的解。所以SVM關注的只有那些最近樣本點,如下圖6中過虛線的那三個點就是支持向量,這也是和邏輯回歸最大的不同,邏輯回歸關注的是所有的樣本點。那麼問題來了,支持向量多還是少的時候,比較好呢?支持向量越多,訓練得到的模型越複雜,就會有過擬合的風險,但是這也不是絕對的。
SMO
對於上面的那個最終式子的求解,這種極值問題,之前邏輯回歸中使用的梯度下降法,但是這種要求的是多個值,使用的就是坐標下降,每次沿着坐標的方向更新一次,就是每個值依次更新,比如在我們這個問題中,我們要更新\(\lambda_1\)的話,我們就需要固定其他的\(\lambda_i\)的值,然後求導進行更新,但是不能忘了我們的問題是有約束條件的,其中\(\sum\limits_{i=1}^{n}\lambda_iy_i = 0\)就說明如果固定其他的話,\(\lambda_1\)就完全等於一個固定的值了,\(\lambda_1 = -\sum\limits_{i=2}^{n}\lambda_iy_i\),不可能再更新啥的。每次更新一個值行不通的話,我們就每次固定住其他值,然後更新倆個值\(\lambda_1\)和\(\lambda_2\),這樣的話,就不會出現上面的情況了,這就是序列最小優化算法SMO的基本思想,其中最小就是最小有倆個。
那麼如何更新這倆個值呢?先來看如何更新最開始的\(\lambda_1\)和\(\lambda_2\),我們拿出最終式,將這個求最大值的式子先轉化為最小值。
\]
我們設置方程\(K(\lambda_1,\lambda_2) = \frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j – \sum\limits_{i=1}^{n}\lambda_i\),然後將這個分解開,其實就是將關於\(\lambda_1\)和\(\lambda_2\)的式子提取出來,因為只有他們倆是未知的,其他都被固定了,可以看成實數。
K(\lambda_1,\lambda_2) & = \frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j – \sum\limits_{i=1}^{n}\lambda_i \notag \\
& = \frac{1}{2}\lambda_1y_1x_1^T\lambda_1y_1x_1+ \lambda_1y_1x_1^T\lambda_2y_2x_2 + \frac{1}{2}\lambda_2y_2x_2^T\lambda_2y_2x_2 – (\lambda_1 + \lambda_2)+\lambda_1y_1\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_1 + \lambda_2y_2\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_2 + C \notag \\
\end{align}
\]
式子中的C就是代表了\(\sum\limits_{i=3}^{n}\lambda_i\),其中\(y_i\)就是標籤,只有1和-1這倆種值,所以\(y_i^2 = 1\),我們將倆個\(x_i\)和\(x_j\)相乘標記為\(k_{ij}\),並且\(v_1 = \sum\limits_{i=3}^{n}\lambda_iy_ix_1x_i, v_2 = \sum\limits_{i=3}^{n}\lambda_iy_ix_2x_i\),那麼上面的式子就可以化簡成
K(\lambda_1,\lambda_2) & = \frac{1}{2}\lambda_1y_1x_1^T\lambda_1y_1x_1+ \lambda_1y_1x_1^T\lambda_2y_2x_2 + \frac{1}{2}\lambda_2y_2x_2^T\lambda_2y_2x_2 – (\lambda_1 + \lambda_2)+\lambda_1y_1\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_1 + \lambda_2y_2\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_2 + C \notag \\
& = \frac{1}{2}\lambda_1^2k_{11}+ \lambda_1\lambda_2y_1y_2k_{12} + \frac{1}{2}\lambda_2^2k_{22} – (\lambda_1 + \lambda_2)+\lambda_1y_1v_1 + \lambda_2y_2v_2 + C \notag \\
\end{align}
\]
因為\(\sum\limits_{i=1}^{n}\lambda_iy_i = 0\),除了\(\lambda_1\)和\(\lambda_2\),其他的都是固定的,那麼\(\lambda_1y_1 + \lambda_2y_2 = \delta\),所以可以表示\(\lambda_1 = y_1(\delta- \lambda_2y_2)\),因此可以帶入式中,式子現在只有一個變量\(\lambda_2\),
\]
可以對\(\lambda\)進行求導,這個求導化簡可以在紙上寫一下,式子很多很長,我怕打錯了,直接寫出化簡的最終式子。
(k_{11} + k_{22} – 2k_{12})\lambda_2 = y_2(y_2 – y_1 + \delta k_{11} – \delta k_{12} + v_1 – v_2)
\]
並且其中的\(\delta = \lambda_1^{old}y_1 + \lambda_2^{old}y_2\),帶入其中進行化簡,為了區分開,將式子左邊的\(\lambda_2\)變成\(\lambda_2^{new}\),設置其中的\(g(x) = \sum\limits_{i=1}^{n}\lambda_iy_ik(x_i,x)+b\),這個\(g(x)\)就代表了預測結果,從上面的\(W\)的求解式可以看出\(g(x) = W^Tx+b\),我們可以使用\(g(x)\)來替換式子中的\(v_i\),那麼\(v_1 = g(x_1) – y_1\lambda_1k_{11} – y_2\lambda_2k_{12}-b\),最終式子化簡變成了
\]
在這個式中,我們需要考慮倆個範圍,第一個就是\(\lambda_i\)的可行域,第二個就是\(k_{11} + k_{22} – 2k_{12}\)的大小。
之前我們提過\(\lambda_1y_1 + \lambda_2y_2 = \delta\),並且\(\lambda_1\)是一個實數,本身就是有範圍的,我們設置為\(0 \leq \lambda_i \leq C\),並且\(\lambda_i\)也是需要滿足\(\lambda_1y_1 + \lambda_2y_2 = \delta\),當\(y_1 = y_2\),那麼\(\lambda_1 + \lambda_2 = \delta\),這邊是1還是-1都是沒有影響,當\(y_1 \ne y_2\),那麼\(\lambda_1 – \lambda_2 = \delta\),我們畫出這倆個式子的圖像,如下圖7所示。
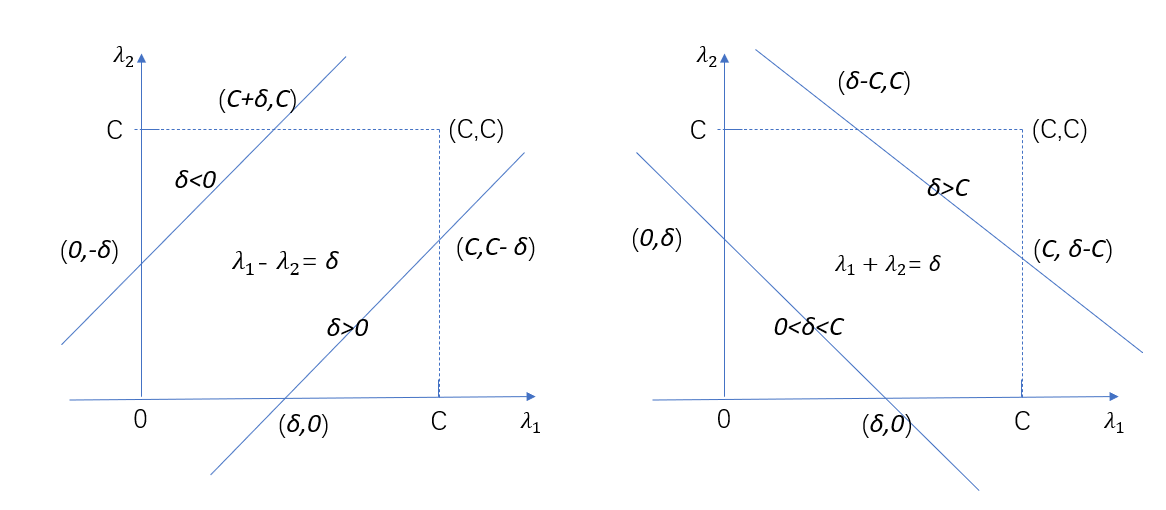
在左圖中,也就是當$y_1 \ne y_2$,$\lambda_1 – \lambda_2 = \delta$的時候,可以看到有倆種情況,第一種情況就是$\delta < 0$,這時$\delta_2 \in [-\delta,C]$,第二種情況就是$\delta > 0$,這時$\delta_2 \in [0,C-\delta]$,那麼最小值$low = max(0,-\delta)$,最大值$high = min(C,C-\delta)$。在右圖中,當$y_1 = y_2$,$\lambda_1 + \lambda_2 = \delta$的時候,也是倆種情況,第一種情況就是$\delta > C$,這時$\delta_2 \in [\delta – C,C]$,第二種情況就是$0 < \delta < C$,這時$\delta_2 \in [0,\delta]$,最小值$low = max(0,\delta)$,最大值$high = min(C,\delta-C)$。所以$low$和$high$是分倆種情況的,這裡我們統一用$low$和$high$表示,在代碼中比較$y_1$和$y-2$即可,這就是它的定義域,因此
$$
\lambda_2^{new} =
\begin{cases}
hight & \lambda_2^{new} > high,\\
\lambda_2^{new} & low \leq \lambda_2^{new} \leq high,\\
low & \lambda_2^{new} < low,\\
\end{cases}
$$
之後我們還需要考慮$k_{11}+k_{22}-2k_{12}$的取值範圍,當它$k_{11}+k_{22}-2k_{12} > 0$,那麼最小值就在可行域中取到,但是如果$k_{11}+k_{22}-2k_{12} \leq 0$,那麼最小值就在邊界$low$和$high$處取到了。
此時\(\lambda_2\)就被計算出來了,下面就是計算\(\lambda_1\),還是通過約束條件\(\lambda_1^{old}y_1 + \lambda_2^{old}y_2 = \lambda_1^{new}y_1 + \lambda_2^{new}y_2\)進行計算,下面就是推導過程。
\lambda_1^{new}y_1 + \lambda_2^{new}y_2 & = \lambda_1^{old}y_1 + \lambda_2^{old}y_2 \notag \\
\lambda_1^{new}y_1 & = \lambda_1^{old}y_1 + \lambda_2^{old}y_2 – \lambda_2^{new}y_2 \notag \\
\lambda_1^{new} & = \lambda_1^{old} + (\lambda_2^{old} – \lambda_2^{new})y_1y_2 \notag \\
\end{align}
\]
在式子\(g(x) = \sum\limits_{i=1}^{n}\lambda_iy_ik(x_i,x)+b\)中也出現了b,那麼我們還可以更新b,因為SMO的本質就是不斷地移動劃分邊界來看誰最好,所以也是需要更新b的。
b_1^{new} & = y_1 – W^Tx_1 \notag \\
& = y_1 – \sum\limits_{i=1}^{n}\lambda_iy_ik_{i1} \notag \\
& = y_1 – \lambda_1^{new}y_1k_{11} – \lambda_2^{new}y_2k_{21} – \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1} \notag \\
\end{align}
\]
我們需要化簡上式中的\(y_1 – \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1}\),我們來看預測差值,也就是
E_1 & = g(x_1) – y_1 \notag \\
& = \sum\limits_{i=1}^{n}\lambda_iy_ik(x_i,x_1)+b^{old} – y_1 \notag \\
& = \lambda_1^{old}y_1k_{11} + \lambda_2^{old}y_2k_{21} + \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1} – y_1 +b^{old} \notag \\
\end{align}
\]
從上式中可以得知\(y_1 – \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1} = -E_1 + \lambda_1^{old}y_1k_{11} + \lambda_2^{old}y_2k_{21} +b^{old}\),因此b中的更新可以進行替換。
b_1^{new} & = -E_1 + \lambda_1^{old}y_1k_{11} + \lambda_2^{old}y_2k_{21} +b^{old} – \lambda_1^{new}y_1k_{11} – \lambda_2^{new}y_2k_{21} \notag \\
& = -E_1 – y_1k_{11}(\lambda_1^{new} – \lambda_1^{old}) + y_2k_{21}(\lambda_2^{new} – \lambda_2^{old}) +b^{old} \notag \\
\end{align}
\]
那麼所有解的推導式子都有了,更新只要根據式子進行更新就行。
上面的式子就能更新,選出倆個\(\lambda_i\),之後根據公式求得\(\lambda_i\),然後進行可行域的判斷,是否超出了上下界,之後更新b。之後在初始選取倆個\(\lambda_i\)方面出現了很多方法,第一個\(\lambda_i\)大多數都是利用KKT條件,也就是選取不滿足KKT條件,那為什麼要選擇呢?這是因為SMO其實就是調整劃分邊界的過程,其中肯定有不滿足\(y_i(W^Tx_i+b) \geq 1\)的存在,如果一個\(\lambda_i\)違背KKT條件程度越大,它就表現得越靠近劃分邊界,最開始的最大值就會越小,它對最開始的最大化函數的減幅也是最大的,所以要先優化它。在代碼中
# 檢查是否滿足KKT條件
if ((labelMat[i]*error < -toler) and (alphas[i] < C)) \
or ((labelMat[i]*error > toler) and (alphas[i] > 0)):
其中labelMat[i]就是數據類別,error就是誤差,表現得就是\(error = W^Tx_i + b – y_i\),toler就是自己設置的容錯率,alphas[i]就是\(\lambda_i\),先看第一個條件,其中的labelMat[i]*error < -toler表明了
y_i(W^Tx_i + b) – 1 + toler < 0 \\
那麼可得y_i(W^Tx_i + b)<1
\]
其中如果有軟間隔的話,下面會講,\(y_i(W^Tx_i + b)<1\)的數據都會被調整到支持向量上,這時\(\lambda_i = C\),但是\(\lambda_i < C\),這樣的數據就不滿足KKT條件了。第二個條件就是labelMat[i]*error > toler,那麼
y_i(W^Tx_i + b) – 1 – toler > 0 \\
那麼可得y_i(W^Tx_i + b)>1
\]
\(y_i(W^Tx_i + b)>1\)代表了它不是支持向量,是那些比較遠的數據,這類數據如果想要滿足KKT條件的話,\(\lambda_i = 0\),但是條件是\(\lambda_i > 0\),那麼自然不滿足KKT條件了。
對於第二個\(\lambda_i\)的選擇,也有很多種方法,其中代表的就是選取與第一個差異最大的數據,能使目標函數有足夠大的變化。
那麼整理一下整個過程:
- 先選取一個\(\lambda_i\),計算它的誤差,查看是否滿足KKT條件(是否被優化);
- 滿足條件,使用方法選擇另外一個\(\lambda_j\),再計算它的誤差;
- 約束\(\lambda_i\)和\(\lambda_j\)的可行域範圍;
- 下面就是求新的\(\lambda_i\)的值了,根據是\(\lambda_i\)新和舊的公式,先計算那個分母,查看它的值;
- 根據公式計算出新的值,優化幅度不大的話,可以結束,進行下一輪;
- 計算出另外一個aj的新值;
- 計算出b的值;
- 如果已經沒有被優化的次數超過了限制次數,說明不用優化了;
軟間隔SVM
到目前為止,我們的SVM還很脆弱,它只能被用在線性可分的數據,並且還不能有噪聲點,這樣的模型是無法使用到現實數據中,因為現實數據的複雜性,會出現很多噪聲點和離群點,
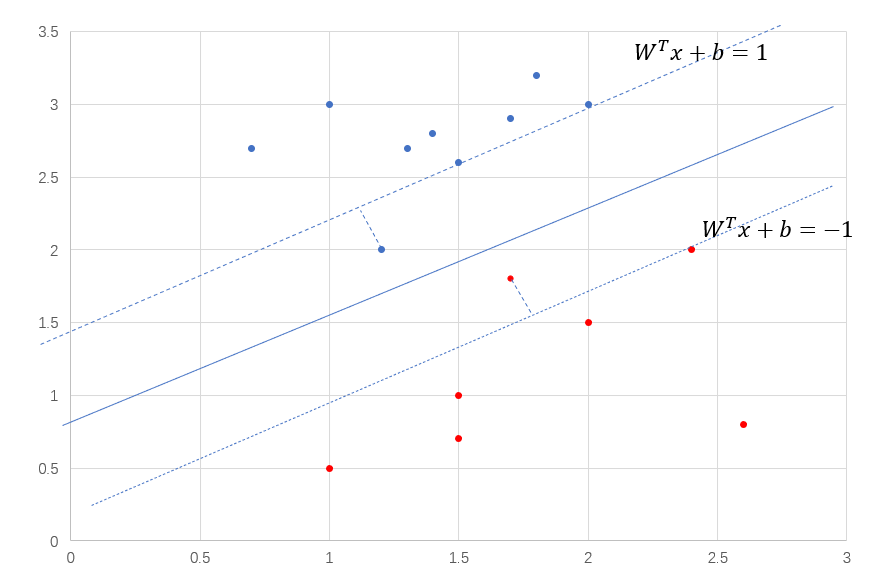
從圖8中看出,SVM的要求很嚴格,即使你分類正確了,也要達到一定的置信度,小於這個置信度,你依然會有損失的存在。我們需要處理這些在虛線內部的點,也就是讓SVM放寬條件,允許模型犯一點小錯誤,讓目標函數加上損失。
\]
關鍵是什麼樣的損失函數能夠滿足SVM?SVM模型只是由支持向量點決定的,對於普通的點,那是沒有任何關係的,所以損失函數也要考慮到這一點,我們可以先來列出要求
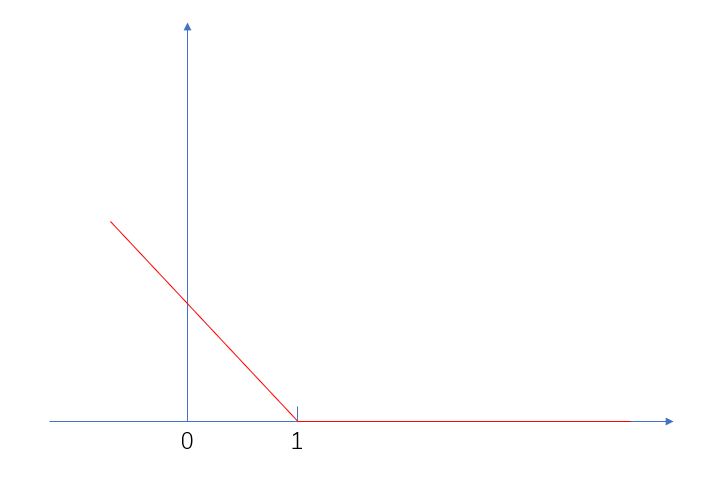
- 如果\(y_i(W^Tx_i + b) \geq 1\),\(loss = 0\)。
- 如果\(y_i(W^Tx_i + b) < 1\),\(loss = 1 – y_i(W^Tx_i + b)\)
這樣的話,我們將之組合起來,變成
\]
這樣就能保持SVM解的稀疏性,我們將之稱為hingle loss,合頁損失。簡單畫一下它的圖像就是
這樣我們就可以將損失帶入到目標函數中,變成
$$
\min\limits_{W,b}\frac{1}{2}|W|^2 + C\sum\limits_{i=1}^nmax\{0, 1-y_i(W^Tx_i + b)\} \\
s.t. y_i(W^Tx_i + b) \geq 1,i=1,2,\dots,n
$$
這樣是可以繼續簡化的,就是將
$$
\xi_i = 1-y_i(W^Tx_i + b), \xi_i \geq 0
$$
目標函數就變成了
$$
\min\limits_{W,b}\frac{1}{2}|W|^2 + C\sum\limits_{i=1}^n\xi_i \\
s.t. y_i(W^Tx_i + b) \geq 1 – \xi_i,i=1,2,\dots,n \\
\xi_i \geq 0
$$
上面這個就是軟間隔SVM的目標函數,它的求解與上面的硬間隔SVM是一樣的。軟間隔SVM是允許有一點點錯誤的數據存在,但是如果數據完全不是線性可分的呢,那麼上面的方法都無法解決,那該如何?
核函數
我們來看一個經典的異或問題,
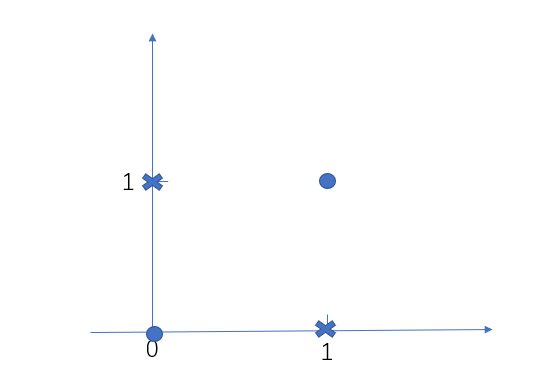
圖中有四個點,原點為一類,叉點為一類,這些數據就不是線性可分,那麼上面的SVM不能應用到這類數據中,這樣的話,我們辛辛苦苦推導了那麼久的SVM,原來這麼雞肋,因為現實中還有更複雜的數據,SVM難道都不行嗎?我們先來看這個異或問題該如何解決,SVM所處理的數據肯定是線性可分的,這一點無法改變,那我們能不能改變其他方面,比如將這些線性不可分的點變成線性可分的點,可以試一試,畢竟實踐出真知,我們將二維變成三維,再加上一個特徵,這個特徵值為$(x_1 – x_2)^2$,那麼其中的叉點變成了(0,1,1)和(1,0,1),圓點變成了(0,0,0)和(1,1,0),畫出這個三維圖像就是
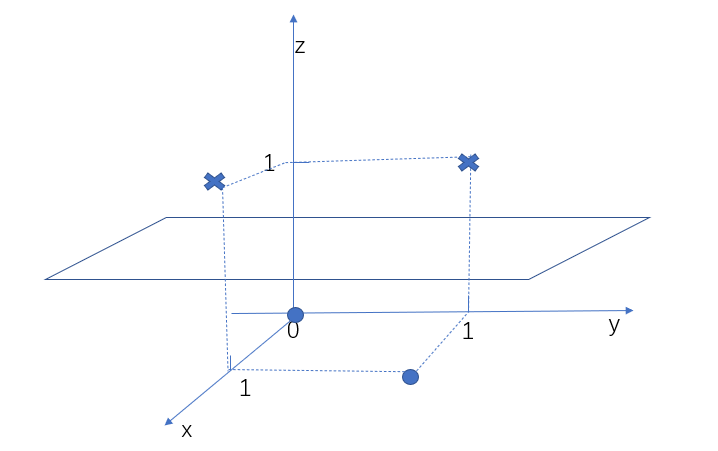
我們可以看到三維之後,數據就變得線性可分了,這也是cover定理,高維比低維更易線性可分,那麼我們可以直接在SVM中將數據更成高維,讓它變得線性可分,這種利用高維線性可分的方法也被稱為核方法,我們將$\phi(x)$稱為數據變成高維的方法,那麼所有的數據$x$都要變成$\phi(x)$,我們上面求出SVM的最終解就變成了
$$
\max\limits_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i \to \max\limits_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_i\phi(x_i)^T\lambda_jy_j\phi(x_j) + \sum\limits_{i=1}^{n}\lambda_i \notag
$$
在很多實際的應用中,$\phi(x)$函數需要將數據變成很高的維度甚至無限維,這樣的話,$\phi(x)$的計算就會變得很複雜,一旦複雜,就很難計算,式中需要先計算$\phi(x_i)^T$,再計算$\phi(x_j)$,最後還要計算倆個式子的乘機$\phi(x_i)^T\phi(x_j)$。一看就知道很複雜,那麼我能不能直接計算出$\phi(x_i)^T\phi(x_j)$的值呢,不用計算其中的$\phi(x_i)^T$和$\phi(x_j)$,當然也是可以的,這種直接計算的技巧被稱為核技巧,那麼我們定義出
$$
K(x_i,x_j) = \phi(x_i)^T\phi(x_j) = <\phi(x_i), \phi(x_j)>
$$
其中$<>$代表內積,$K(x_i,x_j)$就被稱為核函數,在很多文獻中也會嚴格的稱它為正定核函數,而一般核函數的定義就是
$$
K: \chi \times \chi \to R \\
\forall x,z \in \chi,稱K(x,z)為核函數
$$
可以看出一般核函數只要是能將數據映射到實數域中就可以了,並不要求是某個函數的內積。而正定核函數是要求內積的,定義就是
$$
K: \chi \times \chi \to R, \forall x,z \in \chi,有K(x,z), \\
如果\exists \phi: \chi \to R, 並且\phi \in 希爾伯特空間, \\
K(x,z) = <\phi(x), \phi(z)>,那麼稱K(x,z)為正定核函數.
$$
那麼我們怎麼證明一個函數是正定核函數呢?不能用定義來證明啊,也無法證明,那麼就有了下面的條件
$$
K: \chi \times \chi \to R, \forall x,z \in \chi,有K(x,z), \\
如果K(x,z)滿足對稱性和正定性,那麼K(x,z)就是正定核函數。
$$
其中的對稱性就是$K(x,z) = K(z,x)$,而正定性就是任意取N個元素,都是屬於$\chi$,對應的gram matrix是半正定的,而其中的gram matrix就是$G = [K(x_i,x_j)]$,下面就是數學知識了,先來看希爾伯特空間,可能一上來就說希爾伯特空間比較懵,我們先來看最簡單的線性空間,線性空間只定義了數乘與加法,但是我們想研究向量的長度怎麼辦,就加入範式,還想研究向量的角度怎麼辦,就加入內積,變成了內積空間,如果我們還想研究收斂性,就要定義完備性,而完備的內積空間就是希爾伯特空間,完備性就是空間函數的極限還是在希爾伯特空間中,內積也是有對稱性、正定性和線性,其中的對稱性也是上面那種,$
這裡我們例舉出幾個常見的核函數,對於這方面,我的了解也不是很深,
- 線性核,\(K(x_i,x_j) = x_i^Tx_j\),其實就是沒核,還是以前樣子。
- 多項式核,\(K(x_i,x_j) = (x_ix_j + R)^d\),R代表一個設定的數,d就是次方,當d=1的時候,就是線性核。
- 高斯核,也稱為RBF核,\(K(x_i,x_j) = e^{-\frac{|x_i – x_j|^2}{2\sigma^2}}\),這是最常用的核函數。
- 拉普拉斯核,\(K(x_i,x_j) = e^{-\frac{|x_i – x_j|}{\sigma}}\)。
- sigmoid核,\(K(x_i,x_j) = tanh(\beta x_i^Tx_j + \theta)\)。
下面我們看一下最常見的RBF核函數是如何將數據變成無限維的,其中用到了泰勒公式
\]
推導如下:
K(x_i,x_j) & = e^{-\frac{|x_i – x_j|^2}{2\sigma^2}} \notag \\
& = e^{-\frac{x_i^2}{2\sigma^2}} e^{-\frac{x_j^2}{2\sigma^2}} e^{\frac{x_ix_j}{\sigma^2}} \notag \\
& = e^{-\frac{x_i^2}{2\sigma^2}} e^{-\frac{x_j^2}{2\sigma^2}} \sum\limits_{n=0}^{N}\frac{(\frac{x_ix_j}{\sigma^2})^n}{n!} \notag \\
& = \sum\limits_{n=0}^{N} \frac{1}{n!\sigma^{2n}} e^{-\frac{x_i^2}{2\sigma^2}}x_i^n e^{-\frac{x_j^2}{2\sigma^2}}x_j^n \notag \\
& = \sum\limits_{n=0}^{N}(\frac{1}{n!\sigma^{2n}} e^{-\frac{x_i^2}{2\sigma^2}}x_i^n)( \frac{1}{n!\sigma^{2n}}e^{-\frac{x_j^2}{2\sigma^2}}x_j^n) \notag \\
& = \phi(x_i)^T\phi(x_j)
\end{align}
\]
從上面可以看出RBF核函數已經將\(x_i\)和\(x_j\)變成了無限維的
\]
核函數不只是在SVM中應用到,其他機器學習模型中也會用到核函數這一概念,畢竟它的思想都是通用,就是高維比低維更加線性可分。
總結
支持向量機在我的研究中用的很少,主要我一直認為它只用於二分類中,並且我一直對核函數並沒有深入的了解過,對於SVM最新的發展研究也沒有關注過,以前用過一次,就用到我的集成模型中作為我的基學習器,並且也用到了SVM的增量學習,其實我看的是一個中文文獻中的SVM增量學習,算法也是非常簡單,主要還是看後來的數據是不是支持向量,但是後來那個模型失敗了,就沒搞過SVM。本文中所有的代碼都在我的github。

