渲染管线中的顶点变换
概述
在图形学渲染管线中,一个顶点坐标,大概要经历局部坐标系、世界坐标系、相机坐标系、裁剪坐标系,最后到窗口坐标系,显示在屏幕上。
在这些过程中,从一个坐标系到另一个坐标系,都需要进行一定的变换。下面,将介绍每次变换的方式。
注意,本文是针对OpenGL的。
局部空间->世界空间
这一变换过程,主要是将模型放置在世界空间中,进行一定的缩放、旋转或平移。这一步比较简单,只要将相应的矩阵作用到模型的局部空间坐标即可。
比如,对模型缩放(left(S_{x},S_{y},S_{z} right)) ,然后绕Z轴旋转(theta) 度,再进行(left(T_{x},T_{y},T_{z} right)) 的平移。注意,这里的变换顺序是不能变的,即要先进行缩放,再进行旋转,最后进行平移。据此,我们可以构建模型变换矩阵。
[M_{model}= begin{bmatrix} 1 & 0 & 0 & T_{x} \ 0 & 1 & 0 & T_{y} \ 0 & 0 & 1 & T_{z} \ 0 & 0 & 0 & 1 \ end{bmatrix} begin{bmatrix} cos{theta} & -sin{theta} & 0 & 0 \ sin{theta} & cos{theta} & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} begin{bmatrix} S_{x} & 0 & 0 & 0 \ 0 & S_{y} & 0 & 0 \ 0 & 0 & S_{z} & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} ]
世界空间->相机空间
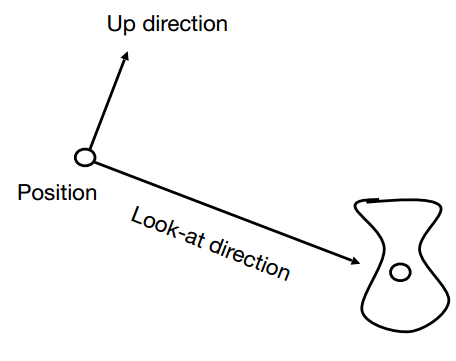
首先定义一下相机:
坐标为(vec{e})
观察方向(vec{g})
向上方向(vec{t})
示意图如下所示:
有一个性质注意一下:当相机和相机“看“到的物体一起变换时,相机”看“到的内容是不变的。 这样,可以将相机的坐标移动到世界坐标的原点,向上方向对齐世界坐标的Y轴,观察方向对齐世界坐标的-Z轴。然后,对物体进行相同的变换即可。
在数学上,这个过程大概这样:
将相机移动到坐标原点
旋转观察方向(vec{g}) 到-Z轴
旋转向上方向(vec{t}) 到Y轴
旋转((vec{g} times vec{t}) )到X轴
大体分为两步:先位移,后旋转。即(M_{view} = R_{view}T_{view}) 。
平移部分:
[T_{view} = begin{bmatrix} 1 & 0 & 0 & -x_{e} \ 0 & 1 & 0 & -y_{e} \ 0 & 0 & 1 & -z_{e} \ 0 & 0 & 0 & 1 \ end{bmatrix} ]
对于旋转部分,先补充一些知识点。对于二维空间来说:
[R_{theta} = begin{pmatrix} cos{theta} & -sin{theta} \ sin{theta} & cos{theta} \ end{pmatrix} ]
[R_{-theta} = begin{pmatrix} cos{theta} & sin{theta} \ -sin{theta} & cos{theta} \ end{pmatrix} = R_{theta}^mathrm{T} ]
根据定义,旋转(theta) 角度和旋转(-theta) 角度是互逆的,即:(R_{-theta} = R_{theta}^{-1}) 。
所以,对于旋转变换,可以得出旋转矩阵的逆等于它的转置,即:
[R_{theta}^mathrm{T} = R_{theta}^{-1} ]
回到上面的旋转部分,直接求相机的坐标轴旋转到世界坐标轴的矩阵不是很方便,但是反过来,求世界坐标轴旋转到相机的坐标轴很容易:
[R_{view}^{-1} = begin{bmatrix} x_{vec{g} times vec{t}} & x_{vec{t}} & x_{-vec{g}} & 0 \ y_{vec{g} times vec{t}} & y_{vec{t}} & y_{-vec{g}} & 0 \ z_{vec{g} times vec{t}} & z_{vec{t}} & z_{-vec{g}} & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} ]
根据旋转矩阵的逆等于它的转置,得出:
[R_{view} = (R_{view}^{-1})^mathrm{T} = begin{bmatrix} x_{vec{g} times vec{t}} & y_{vec{g} times vec{t}} & z_{vec{g} times vec{t}} & 0 \ x_{vec{t}} & y_{vec{t}} & z_{vec{t}} & 0 \ x_{-vec{g}} & y_{-vec{g}} & z_{-vec{g}} & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} ]
根据(M_{view} = R_{view}T_{view}) ,可以得出:
[M_{view} = R_{view}T_{view} = begin{bmatrix} x_{vec{g} times vec{t}} & y_{vec{g} times vec{t}} & z_{vec{g} times vec{t}} & 0 \ x_{vec{t}} & y_{vec{t}} & z_{vec{t}} & 0 \ x_{-vec{g}} & y_{-vec{g}} & z_{-vec{g}} & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} begin{bmatrix} 1 & 0 & 0 & -x_{e} \ 0 & 1 & 0 & -y_{e} \ 0 & 0 & 1 & -z_{e} \ 0 & 0 & 0 & 1 \ end{bmatrix} ]
相机空间->裁剪空间
在一个顶点着色器运行的最后,期望所有的坐标都能落在一个特定的范围内,且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略,所以剩下的坐标就将变为屏幕上可见的片段。这也就是裁剪空间(Clip Space)名字的由来。
因为将所有可见的坐标都指定在-1.0到1.0的范围内不是很直观,所以我们会指定自己的坐标集(Coordinate Set)并将它变换回标准化设备坐标系。
由投影矩阵创建的观察箱(Viewing Box)被称为平截头体(Frustum),每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将特定范围内的坐标转化到标准化设备坐标系的过程(而且它很容易被映射到2D观察空间坐标)被称之为投影(Projection),因为使用投影矩阵能将3D坐标投影(Project)到很容易映射到2D的标准化设备坐标系中。
这里要注意一下,OpenGL是右手坐标系的,但是在NDC中,是左手坐标系的,这里要特别注意!!!
相机空间转换到裁剪空间,有需要用到投影变换。有两种投影变换:正交投影和透视投影。下面分别介绍一下。
正交投影
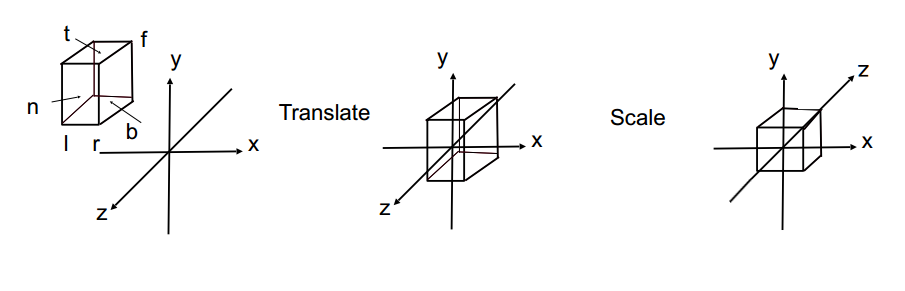
我们先定义一个正交投影的视锥体([l,r] times [b,t] times [f,n]) (注意,n和f都是负数,f是远平面,所以f<n),它是一个长方体。我们需要做的,就是将正交投影的视锥体转换到标准立方体(即标准化设备坐标,([-1,1]^{3}) )。注意,这里([f,n]) 映射到NDC中的[1,-1]。
这里,分成两个步骤:平移和缩放。正交投影的矩阵如下:
[M_{ortho} = begin{bmatrix} frac{2}{r-l} & 0 & 0 & 0 \ 0 & frac{2}{t-b} & 0 & 0 \ 0 & 0 & frac{2}{f-n} & 0 \ 0 & 0 & 0 & 1 \ end{bmatrix} begin{bmatrix} 1 & 0 & 0 & -frac{r+l}{2} \ 0 & 1 & 0 & -frac{t+b}{2} \ 0 & 0 & 1 & -frac{n+f}{2} \ 0 & 0 & 0 & 1 \ end{bmatrix}= begin{bmatrix} frac{2}{r-l} & 0 & 0 & -frac{r+l}{r-l} \ 0 & frac{2}{t-b} & 0 & -frac{t+b}{t-b} \ 0 & 0 & frac{2}{f-n} & -frac{f+n}{f-n} \ 0 & 0 & 0 & 1 \ end{bmatrix} ]
透视投影
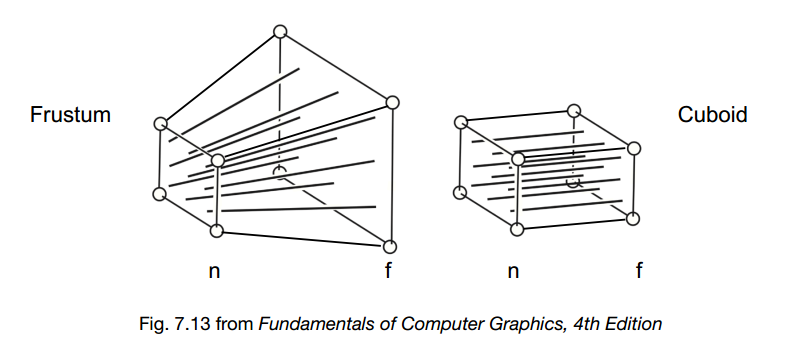
对于透视投影,分成两步操作:
首先,“压扁”视锥体成一个长方体(n->n,f->f)((M_{persp->ortho}) );
然后,做正交投影操作((M_{ortho}) ,即上面的正交投影)。
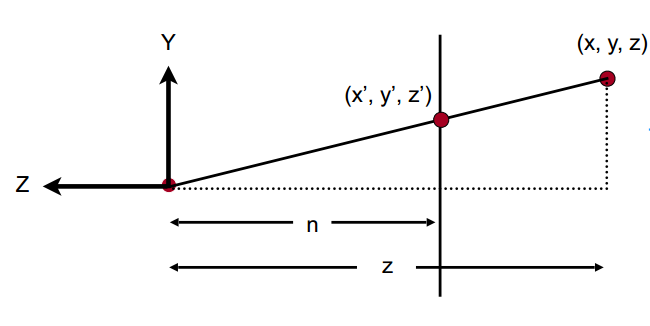
观察下图:
根据相似三角形的关系,可以得出:
[y^{‘} = frac{n}{z}y ]
类似的,可以得出:
[x^{‘} = frac{n}{z}x ]
由此,可以得出下面的关系:
[M_{persp->ortho}^{(4 times 4)} begin{pmatrix} x\ y\ z\ 1\ end{pmatrix}= begin{pmatrix} frac{n}{z}x \ frac{n}{z}y \ unknown \ 1 \ end{pmatrix} ]
下面,说一个齐次坐标的性质:在3D坐标系统中,(left ( x,y,z,1 right )) ,(left ( kx,ky,kz,k neq 0 right )) ,(left ( xz,yz,z^{2},z neq 0 right )) 都表示相同的坐标—(left ( x,y,z right )) 。例如:(left ( 1,0,0,1 right )) 和(left ( 2,0,0,2 right )) 都表示坐标(left ( 1,0,0 right )) 。
所以,有如下关系:
[M_{persp->ortho}^{(4 times 4)} begin{pmatrix} x\ y\ z\ 1\ end{pmatrix}= begin{pmatrix} frac{n}{z}x \ frac{n}{z}y \ unknown \ 1 \ end{pmatrix} = begin{pmatrix} nx \ ny \ unknown \ z \ end{pmatrix} ]
更进一步的,可以得到:
[M_{persp->ortho} = begin{pmatrix} n & 0 & 0 & 0 \ 0 & n & 0 & 0 \ ? & ? & ? & ? \ 0 & 0 & 1 & 0 \ end{pmatrix} ]
现在,还剩下第三列是未知的。
经过观察上面的透视投影视锥体,可以得出以下推论:
近平面上的点的坐标都不会改变;
远平面上的点,Z坐标不改变。
根据推论1,近平面上的点(left (x,y,n,1 right )) 经过变换后,不会改变。即:
[M_{persp->ortho} begin{pmatrix} x \ y \ n \ 1 \ end{pmatrix} = begin{pmatrix} x \ y \ n \ 1 \ end{pmatrix} = begin{pmatrix} nx \ ny \ n^{2} \ n \ end{pmatrix} ]
根据:
[M_{persp->ortho} begin{pmatrix} x\ y\ z\ 1\ end{pmatrix}= begin{pmatrix} nx \ ny \ unknown \ z \ end{pmatrix} ]
因为(n^{2}) 与x和y都没有关系,所以可以得出(M_{persp->ortho}) 的第三列的形式是(left (0,0,A,B right )) 。
根据:
[left(0,0,A,B right) begin{pmatrix} x \ y \ n \ 1 \ end{pmatrix} = n^{2} ]
可以得出:
[An+B = n^{2} ]
根据推论2,远平面的中心点(left (0,0,f,1 right)) ,经过变换后,还是本身。如下:
[M_{persp->ortho} begin{pmatrix} 0 \ 0 \ f \ 1 \ end{pmatrix} = begin{pmatrix} 0 \ 0 \ f \ 1 \ end{pmatrix} = begin{pmatrix} 0 \ 0 \ f^{2} \ f \ end{pmatrix} ]
所以,可以得出:
[left(0,0,A,B right) begin{pmatrix} 0 \ 0 \ f \ 1 \ end{pmatrix} = f^{2} ]
即:
[Af + B = f^{2} ]
到这里,可以得出方程组:
[begin{cases} An + B = n^{2} \ Af + B = f^{2} \ end{cases} Rightarrow begin{matrix} A = n + f \ B = -nf \ end{matrix} ]
到这里,可以得出(M_{persp->ortho}) :
[M_{persp->ortho} = begin{bmatrix} n & 0 & 0 & 0 \ 0 & n & 0 & 0 \ 0 & 0 & n+f & -nf \ 0 & 0 & 1 & 0 \ end{bmatrix} ]
最终,透视投影矩阵:
[M_{persp} = M_{ortho}M_{persp->ortho} = begin{bmatrix} frac{2n}{r-l} & 0 & frac{l+r}{l-r} & 0 \ 0 & frac{2n}{t-b} & frac{b+t}{b-t} & 0 \ 0 & 0 & frac{f+n}{f-n} & frac{2nf}{n-f} \ 0 & 0 & 1 & 0 \ end{bmatrix} ]
裁剪空间->窗口空间
在裁剪空间的最后,所以的可见的点都在标准设备坐标系(NDC)中,即坐标坐落在范围([-1,1]^{3}) 内。
先不考虑Z轴的变换。
从NDC到窗口空间,需要经过视口变换。定义一个屏幕空间:(left (0,0,w,h right)) 。平面左下角的坐标位(left (0,0 right)) ,右上角的坐标为(left (w,h right)) 。对于X和Y坐标的变换,即从(left(-1,1right) times left(-1,1right)) 到(left(0,wright) times left(0,hright)) 。
这里,经过两步变换:
将NDC的中心平移到窗口的中心;
[T_{viewport} = begin{pmatrix} 1 & 0 & 0 & frac{w}{2} \ 0 & 1 & 0 & frac{h}{2} \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ end{pmatrix} ]
将NDC的大小缩放到屏幕的大小。
[R_{viewport} = begin{pmatrix} frac{w}{2} & 0 & 0 & 0 \ 0 & frac{h}{2} & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ end{pmatrix} ]
合并到一起:
[M_{viewport} = R_{viewport}T_{viewport} = begin{pmatrix} frac{w}{2} & 0 & 0 & frac{w}{2} \ 0 & frac{h}{2} & 0 & frac{h}{2} \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ end{pmatrix} ]
对于Z坐标,从(left(-1,1right)) 映射到了(left(0,1right)) 。这里只是简单的线性映射。假设(z^{‘} = Az+B) ,当(z) 等于-1时,(z^{‘}) 等于0;当(z) 等于1时,(z^{‘}) 等于1。可得如下方程组:
[begin{cases} A(-1) + B = 0 \ A(1) + B = 1 \ end{cases} Rightarrow begin{cases} A = frac{1}{2} \ B = frac{1}{2} \ end{cases} ]
所以,(z^{‘} = frac{1}{2}z + frac{1}{2}) 。代入上述(M_{viewport}) 矩阵,可得:
[M_{viewport} = begin{pmatrix} frac{w}{2} & 0 & 0 & frac{w}{2} \ 0 & frac{h}{2} & 0 & frac{h}{2} \ 0 & 0 & frac{1}{2} & frac{1}{2} \ 0 & 0 & 0 & 1 \ end{pmatrix} ]
参考