数据结构高阶–八大排序汇总
排序总览
什么是排序?
🔥排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
✍️排序的稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
排序的分类
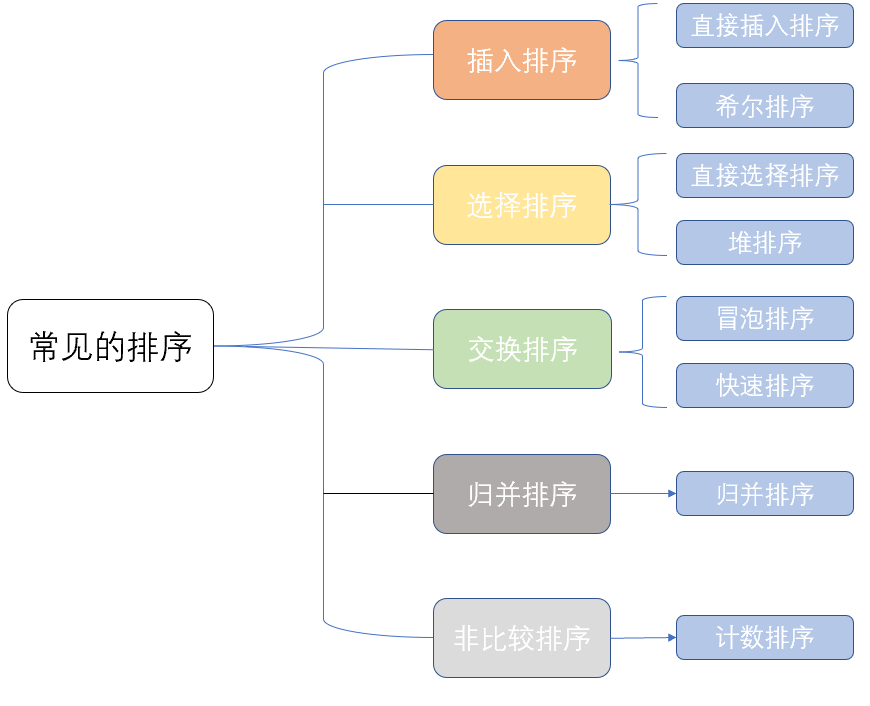
插入排序
直接插入排序
⛅基本思想:把待排序的数逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
✍️一般地,我们把第一个看作是有序的,所以我们可以从第二个数开始往前插入,使得前两个数是有序的,然后将第三个数插入直到最后一个数插入
口头说还是太抽象了,那么我们用一个具体例子来介绍一下吧

所以直接插入排序的代码实现如下:
void InsertSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)
{
int end = i;
//先定义一个变量,将要插入的数保存起来
int x = a[end + 1];
//直到后面的数比前面大的时候就不移动,就直接把这个数放在end的后面
while (end >= 0)
{
if (a[end] > x)
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = x;
}
}
时间复杂度和空间复杂度
⛅时间复杂度: 第一趟end最多往前移动1次,第二趟是2次……第n-1趟是n-1次,所以总次数是1+2+3+……+n-1=n*(n-1)/2,所以说时间复杂度是O(n^2)
最好的情况: 顺序
最坏的情况: 逆序
⛅空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
直接插入排序稳定性
✍️直接插入排序在遇到相同的数时,可以就放在这个数的后面,就可以保持稳定性了,所以说这个排序是稳定的。
希尔排序
🐾基本思想:希尔排序是建立在直接插入排序之上的一种排序,希尔排序的思想上是把较大的数尽快的移动到后面,把较小的数尽快的移动到后面。先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。(直接插入排序的步长为1),这里的步长不为1,而是大于1,我们把步长这个量称为gap,当gap>1时,都是在进行预排序,当gap==1时,进行的是直接插入排序
🔥同样的我们看图说话!
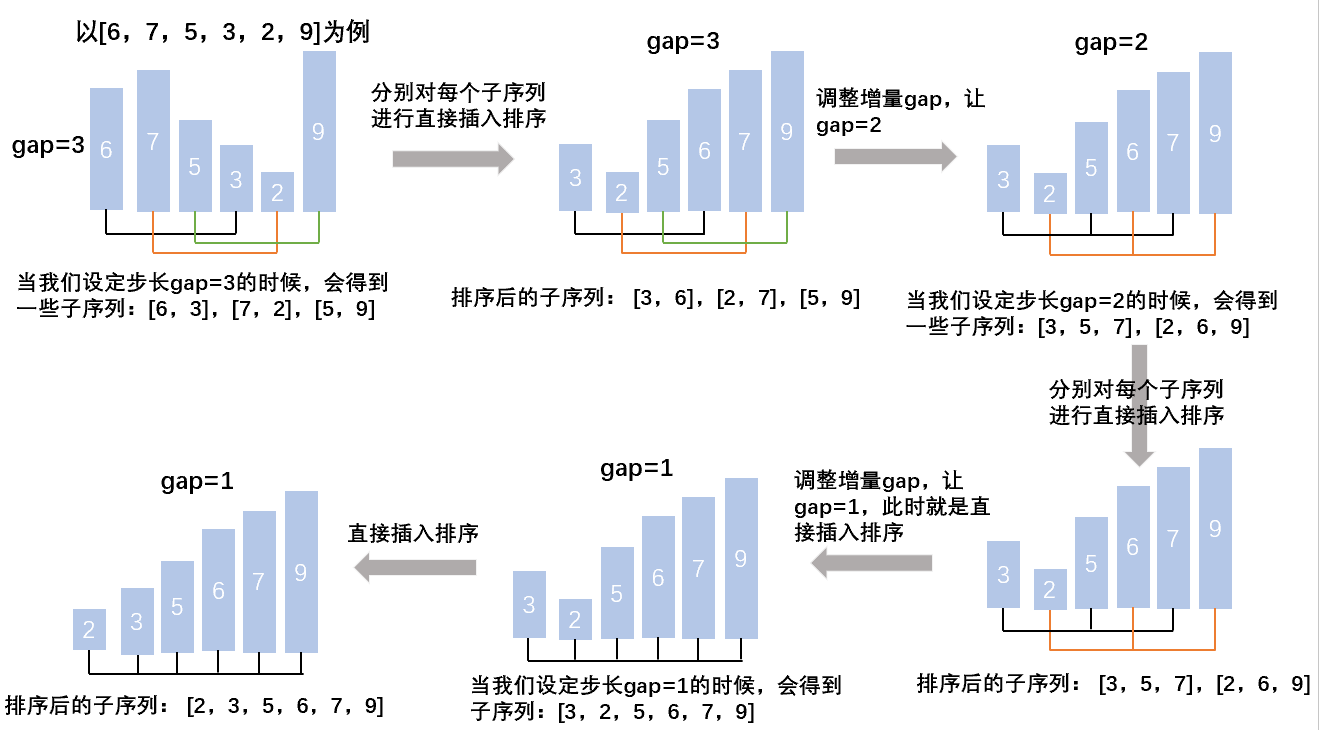
我们先来一个单趟的排序:
int end = 0;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end =end - gap;
}
else
{
break;
}
}
a[end + gap] = x;
这里的单趟排序的实现和直接插入排序差不多,只不过是原来是gap = 1,现在是gap了。
由于我们要对每一组都进行排序,所以我们可以一组一组地排,像这样:
// gap组
for (int j = 0; j < gap; j++)
{
int i = 0;
for (i = 0; i < n-gap; i+=gap)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
}
也可以对代码进行一些优化,直接一起排序,不要一组一组地,代码如下:
int i = 0;
for (i = 0; i < n - gap; i++)// 一起预排序
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
当gap>1时,都是在进行预排序,当gap==1时,进行的是直接插入排序。
- gap越大预排越快,预排后越不接近有序
- gap越小预排越慢,预排后越接近有序
- gap==1时,进行的是直接插入排序。
- 所以接下来我们要控制gap,我们可以让最初gap为n,然后一直除以2直到gap变成1,也可以这样:gap = gap/3+1。只要最后一次gap为1就可以了。
所以最后的代码实现如下:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)// 不要写等于,会导致死循环
{
// gap > 1 预排序
// gap == 1 插入排序
gap /= 2;
int i = 0;
for (i = 0; i < n - gap; i++)// 一起预排序
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
}
}
时间复杂度和空间复杂度
⛅时间复杂度:外层的循环次数,复杂度是O(logN)
每一组的数的个数大概是N/gap,总共有N/n/gap个组,所以调整的次数应该是(1+2+……+N/gap-1)*gap,所以我们分成两种极端来看待这个问题:
当gap很大,也就是gap = N/2的时候,调整的次数是N/2,也就是O(N)
当gap很小,也就是gap = 1的时候,按道理来讲调整的次数应该(1+2+……+N-1)*gap,应该是O(n^2),但是这时候应该已经接近有序,次数没有那么多,所以我们不如就看作时间复杂度为O(N)
综上:希尔排序的时间复杂度应该是接近O(N*logN)
⛅空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
希尔排序稳定性
✍️我们可以这样想,相同的数被分到了不同的组,就不能保证原有的顺序了,所以说这个排序是不稳定的。
选择排序
直接选择排序
🐾基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
🔥同样的我们看图说话!

整体排序就是begin往前走,end往后走,相遇就停下,所以整体代码实现如下:
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin;
int maxi = begin;
int i = 0;
for (i = begin; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
// 如果maxi和begin相等的话,要对maxi进行修正
if (maxi == begin)
{
maxi = mini;
}
swap(a[begin], a[mini]);
swap(a[end], a[maxi]);
begin++;
end--;
}
}
}
这里说明一下,其中加了一段修正maxi的代码,就是为了防止begin和maxi相等时,mini与begin交换会导致maxi的位置发生变化,而此时begin就是maxi,若此时交换maxi和end,换到end处的不是最大值,而是最小值mini,所以提前将mini赋值给maxi,当begin与mini交换的时候,mini处就是begin也就是最大值,这样maxi与end交换就不会出现错误
时间复杂度和空间复杂度
⛅ 时间复杂度:第一趟遍历n-1个数,选出两个数,第二趟遍历n-3个数,选出两个数……最后一次遍历1个数(n为偶数)或2个数(n为奇数),所以总次数是n-1+n-3+……+2,所以说时间复杂度是O(n^2)
✍️最好的情况: O(n^2)(顺序)
✍️最坏的情况: O(n^2)(逆序)
⛅空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
选择排序稳定性
直接选择排序是不稳定的
举个例子:假设顺序是3 2 3 0,遍历选出最小的0,此时0与3交换,两个3的前后顺序明显发生了变化,所以是不稳定的
堆排序
数据结构初阶–堆排序+TOPK问题 – 一只少年a – 博客园 (cnblogs.com)
这篇已经介绍过了
补充一点:堆排序是不稳定的
交换排序
冒泡排序
🐾基本思想:它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成(依次向后比较两个元素,将大的元素放到后面)
🔥同样的我们看图说话!
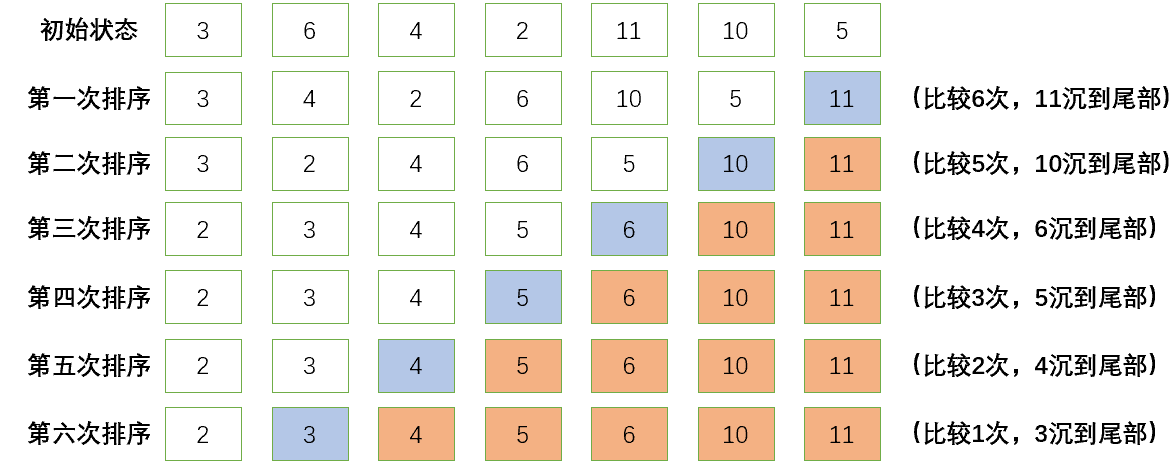
冒泡排序整体代码实现如下:
void BubbleSort(int* a, int n)
{
int i = 0;
//外层循环,需要进行几次排序
for (i = 0; i < n - 1; i++)
{
int j = 0;
//内部循环,比较次数
for (j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
swap(a[j], a[j + 1]);
}
}
}
}
✍️我们思考一个问题,假设当前的序列已经有序了,我们有没有什么办法直接结束排序?就像图中的情况,在第三次排序的时候已经有序,后面的比较是没必要的
这当然是有的,我们可以定义一个exchange的变量,如果这趟排序发生交换就把这个变量置为1,否则就不变,不发生交换的意思就是该序列已经有序了,利用这样一个变量我们就可以直接结束循环了
优化后的冒泡排序代码:
void BubbleSort(int* a, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)
{
int exchange = 0;
int j = 0;
for (j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
exchange = 1;
Swap(&a[j], &a[j + 1]);
}
}
// 不发生交换
if (exchange == 0)
break;
}
}
时间复杂度和空间复杂度
⛅时间复杂度: 第一趟最多比较n-1次,第二趟最多比较n-2次……最后一次最多比较1次,所以总次数是n-1+n-2+……+1,所以说时间复杂度是O(n^2)
最好的情况: O(n)(顺序)
最坏的情况: O(n^2)(逆序)
⛅空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
冒泡排序稳定性
✍️冒泡排序在比较遇到相同的数时,可以不进行交换,这样就保证了稳定性,所以说冒泡排序数稳定的。
快速排序(递归版本)
🐾基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
✍️快速排序的基本流程
- 首先在待排序列中确定一个基准值,遍历整个序列,将小于(可包含等于)基准值的元素放到基准值左边,将大于(可包含等于)基准值的元素放到其右边。(降序序列可将位置调整)
- 此时基准值将序列分割成俩个部分,左边的元素全部小于基准值,右边的元素全部大于基准值
- 将分割的左右俩部分进行如上俩步操作,实则为递归
- 通过递归将左右俩侧排好序,直至分割的小序列个数为1,排序全部完成
hoare版本
🐾基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
🔥同样的我们看图说话!

🌰我们要遵循一个原则:关键词取左,右边先找小再左边找大;关键词取右,左边找先大再右边找小。
🌰一次过后,2也就来到了排序后的位置,接下来我们就是利用递归来把key左边区间和右边的区间递归排好就可以了,如下:
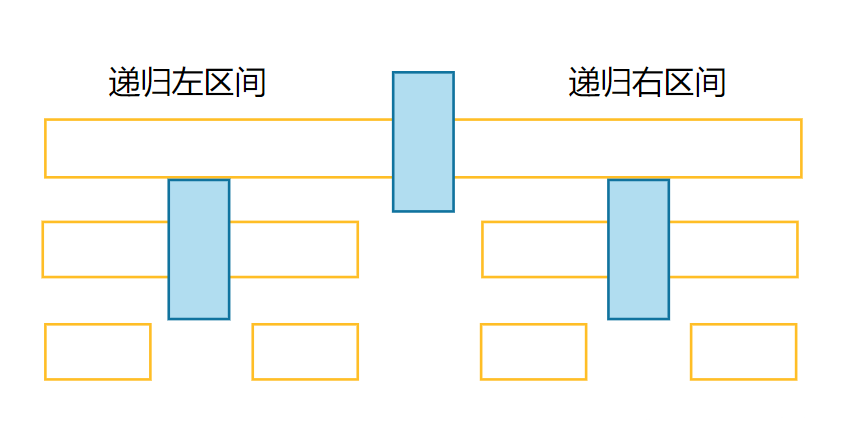
递归左区间:[left, key-1] key 递归右区间:[key+1, right]
hoare版本找key值代码实现如下:
int PartSort1(int* a, int left, int right)
{
int key = left;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= a[key])
{
right--;
}
// 左边找大
while (left < right && a[left] <= a[key])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}
快排代码实现如下:
void QuickSort(int* a, int left, int right)
{
if (left > right)
return;
int div = PartSort1(a, left, right);
// 两个区间 [left, div-1] div [div+1, right]
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
}
✍️我们考虑这样一种情况,当第一个数是最小的时候,顺序的时候会很糟糕,因为每次递归right都要走到头,看下图:
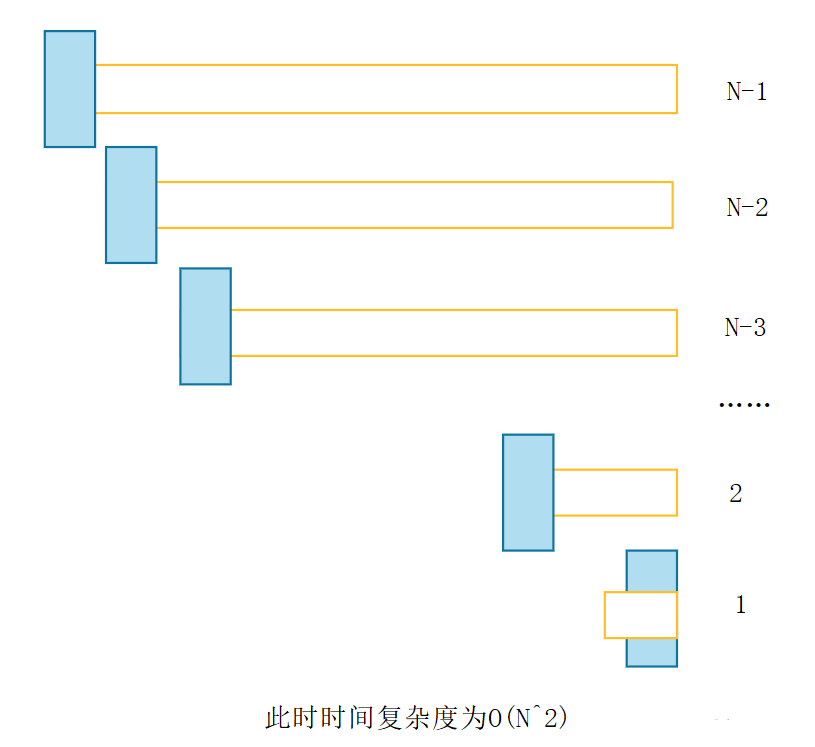
为了优化这里写了一个三数取中的代码,三数取中就是在序列的首、中和尾三个位置选择第二大的数,然后放在第一个位置,这样就防止了首位不是最小的,这样也就避免了有序情况下,情况也不会太糟糕。
下面是三数取中代码:
int GetMidIndex(int* a, int left, int right)
{
int mid = left + (right - left) / 2;
if (a[mid] > a[left])
{
if (a[right] > a[mid])
{
return mid;
}
// a[right] <= a[mid]
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
// a[mid] <= a[left]
else
{
if (a[mid] > a[right])
{
return mid;
}
// a[mid] <= a[right]
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
所以加上三数取中优化后的代码如下:
int PartSort1(int* a, int left, int right)
{
int index = GetMidIndex(a, left, right);
Swap(&a[index], &a[left]);
int key = left;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= a[key])
{
right--;
}
// 左边找大
while (left < right && a[left] <= a[key])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}
挖坑法
🐾基本思想:设定一个基准值(一般为序列的最左边元素,也可以是最右边的元素)此时最左边的是一个坑。开辟两个指针,分别指向序列的头结点和尾结点(选取的基准值在左边,则先从右边出发。反之,选取的基准值在右边,则先从左边出发)。 从右指针出发依次遍历序列,如果找到一个值比所选的基准值要小,则将此指针所指的值放在坑里,左指针向前移。 后从左指针出发(选取的基准值在左边,则后从左边出发。反之,选取的基准值在右边,则后从右边出发),依次便利序列,如果找到一个值比所选的基准值要大,则将此指针所指的值放在坑里,右指针向前移。 依次循环步骤,直到左指针和右指针重合时,我们把基准值放入这两个指针重合的位置。
🔥同样的我们看图说话!
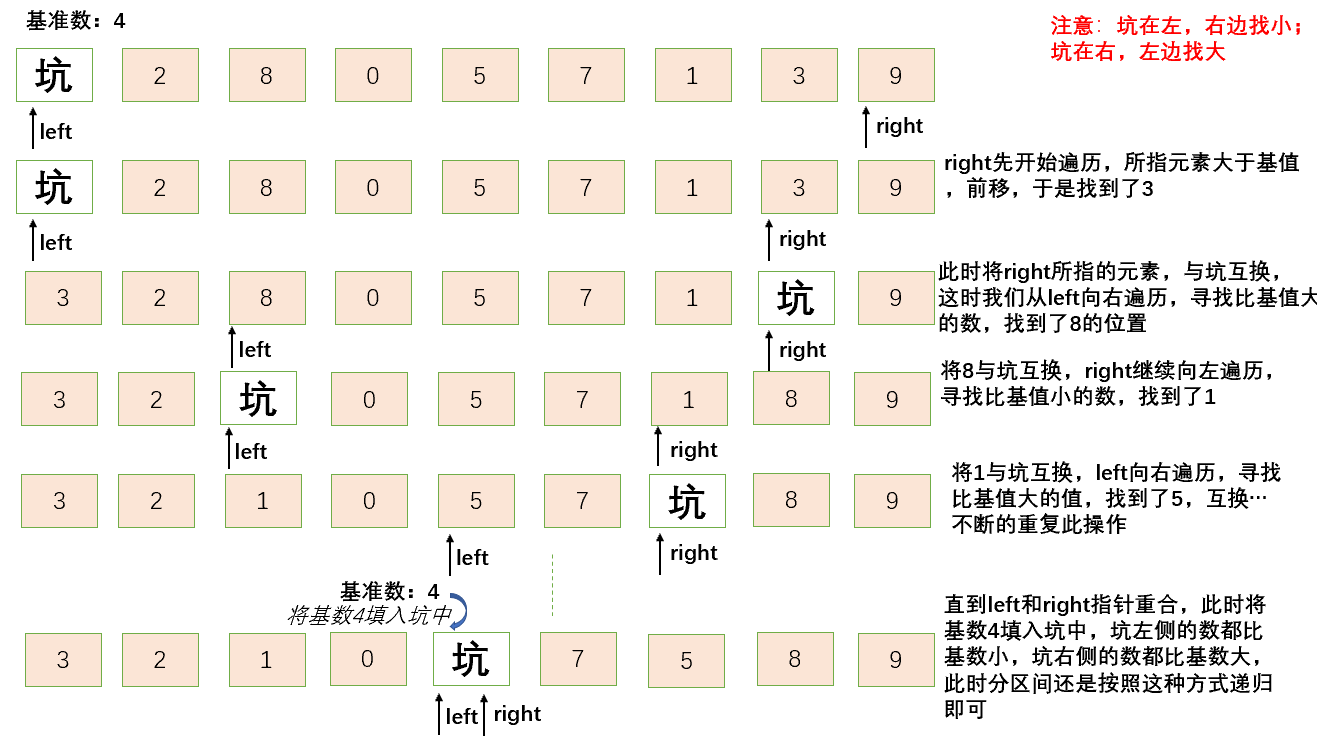
挖坑法我们要遵循一个原则:坑在左,右边找小;坑在右,左边找大。
挖坑法代码实现如下(加了三数取中算法):
int PartSort2(int* a, int left, int right)
{
int index = GetMidIndex(a, left, right);
Swap(&a[index], &a[left]);
//pivot就是那个坑
int pivot = left;
int key = a[pivot];
while (left < right)
{
// 坑在左边,右边找小
while (left < right && a[right] >= key)
{
right--;
}
Swap(&a[pivot], &a[right]);
pivot = right;
// 坑在右边边,右边找大
while (left < right && a[left] <= key)
{
left++;
}
Swap(&a[pivot], &a[left]);
pivot = left;
}
a[pivot] = key;
return pivot;
}
前后指针法
🐾基本思想:前后指针法就是有两个指针prev和cur,cur个在前,prev在后,cur在前面找小,找到了,prev就往前走一步,然后交换prev和cur所在位置的值,然后cur继续找小,直到cur走到空指针的位置就结束,最后将prev的值与key交换就完成了一次分割区间的操作
🔥同样的我们看图说话!
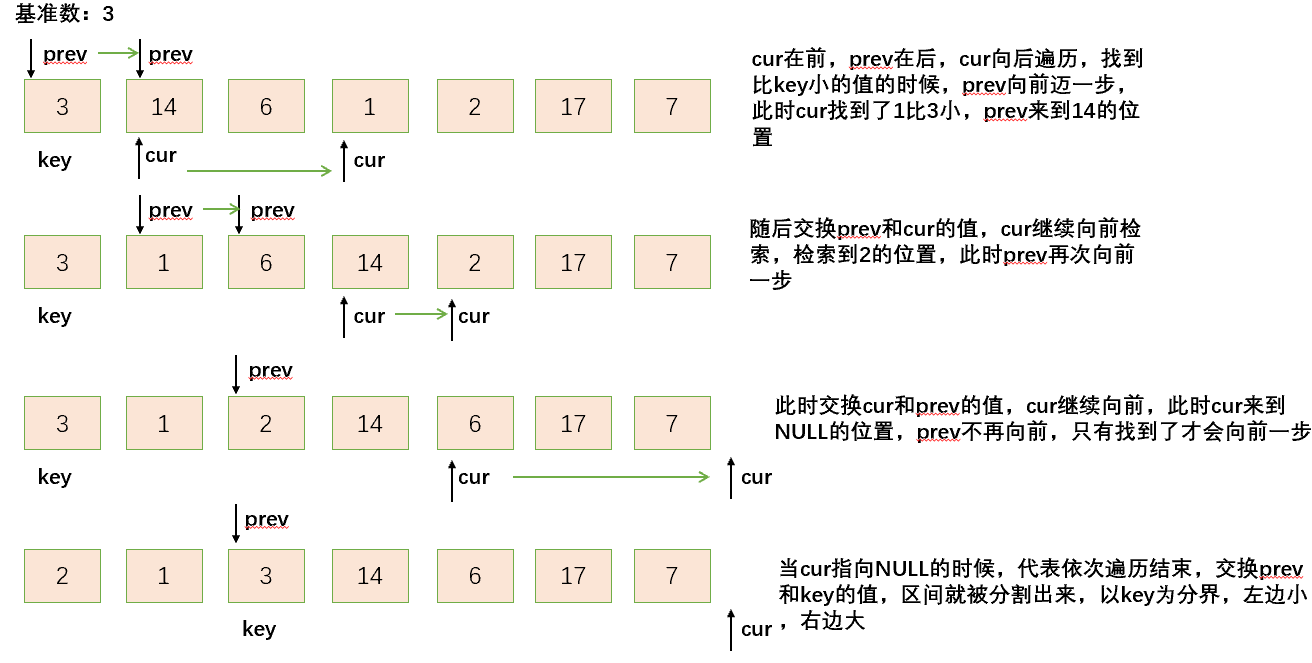
代码实现:
int PartSort3(int* a, int left, int right)
{
int index = GetMidIndex(a, left, right);
Swap(&a[index], &a[left]);
int key = a[left];
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < key)
{
prev++;
if (prev != cur)
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[prev], &a[left]);
return prev;
}
小区间优化快速排序
🐾小区间优化原理:当快速排序在递归过程中一直切分区间时,最后会被分成很小的区间,当区间中的数据个数很小时,其实这是已经是没有必要进行再分割的,且最后一层基本上占据了快速排序一半的递归,这是我们可以选择其他的排序来解决这个小区间的排序
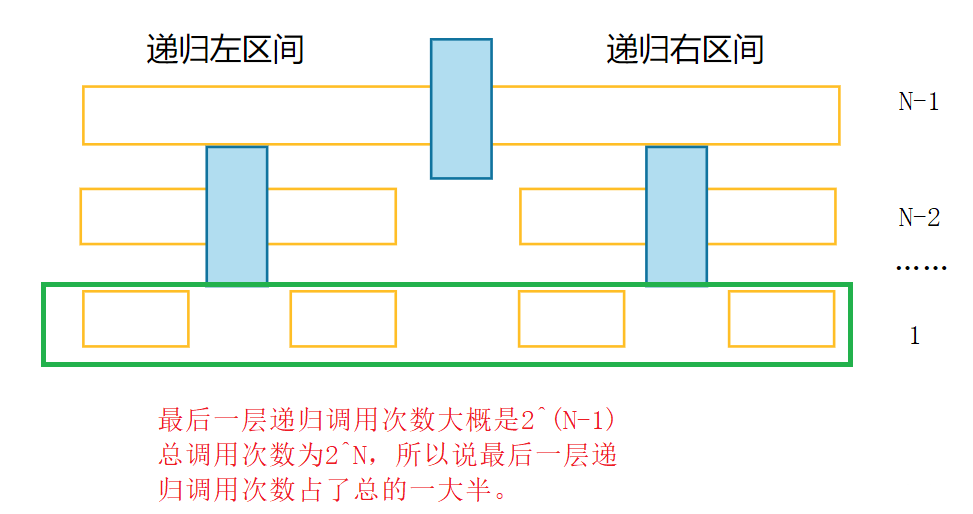
🐾还有一个我们要思考的问题就是最后这段小区间用什么排序比较好?
希尔排序适应的是比较多的数据才有优势,堆排序也不行,需要建堆,有点杀鸡用牛刀的感觉,其他三个插入排序、选择排序和冒泡排序相比,还是插入排序比较优,所以我们小区间选择用插入排序进行排序
void QuickSort(int* a, int left, int right)
{
if (left > right)
return;
int div = PartSort3(a, left, right);
// 两个区间 [left, div-1] div [div+1, right]
if (div - 1 - left > 10)
{
QuickSort(a, left, div - 1);
}
else
{
InsertSort(a + left, (div - 1) - left + 1);
}
if (right - div - 1 > 10)
{
QuickSort(a, div + 1, right);
}
else
{
InsertSort(a + div + 1, right - (div + 1) + 1);
}
}
快速排序(非递归版本)
🐾 基本思想:利用栈来模拟实现递归调用的过程,利用压栈的顺序来实现排序的顺序。
给大家看一个利用栈模拟实现的动图
🔥同样的我们看图说话!
我们拿数组arr=[5,2,4,7,9,1,3,6]来举个例子:
第一步:我们先把区间的右边界值7进行压栈,然后把区间的左边界值0进行压栈,那我们取出时就可以先取到左边界值,后取到后边界值
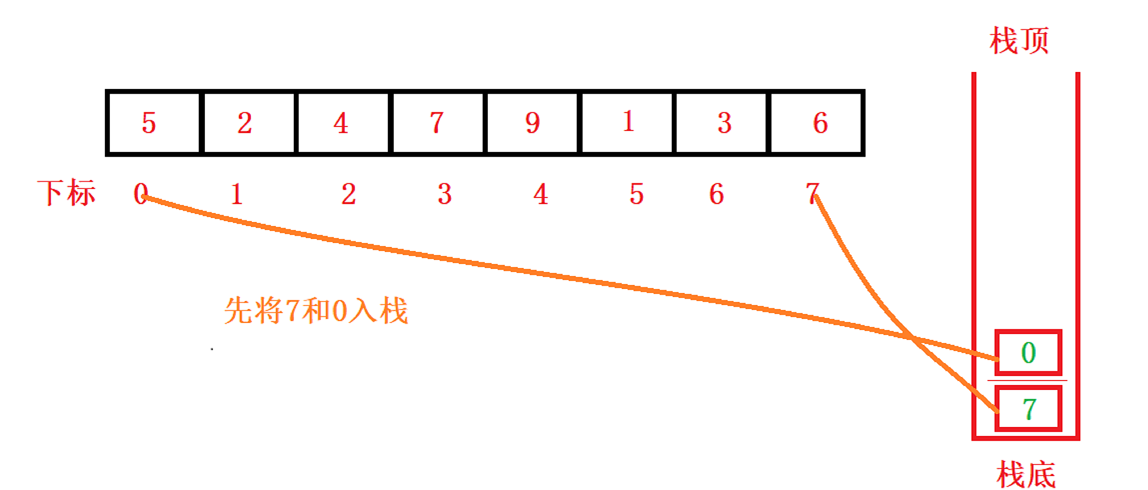
第二步:我们获取栈顶元素,先取到0给left,后取到7给right,进行单趟排序

第三步:第一趟排完后,区间被分为左子区间和右子区间。为了先处理左边,所以我们先将右子区间压栈,分别压入7和5,然后压入左子区间,3和0

第四步:取出0和3进行单趟排序

第五步:此时左子区间又被划分为左右两个子区间,但是右子区间只有4一个值,不再压栈,所以只入左子区间,将1和0压栈

第六步:取出0和1进行单趟排序

第七步:至此,左子区间全部被排完,这时候才可以出5和7排右子区间,是不是很神奇?这个流程其实和递归是一模一样的,顺序也没变,但解决了递归的致命缺陷——栈溢出。后面的流程就不一一展现了
void QuickSortNonR(int* a, int left, int right)
{
stack<int> s;
s.push(right);
s.push(left);
while (!s.empty())
{
int newLeft = s.top();
s.pop();
int newRight = s.top();
s.pop();
//挖洞法
int div = PartSort2(a, newLeft, newRight);
// 两个区间 [left, div-1] div [div+1, right]
// 压右区间
if (div + 1 < newRight)
{
s.push(newRight);
s.push(div + 1);
}
// 压左区间
if (newLeft < div - 1)
{
s.push(div - 1);
s.push(newLeft);
}
}
}
快速排序时间复杂度和空间复杂度
⛅空间复杂度:
最优的情况下空间复杂度为:O(logN) ;每一次都平分数组的情况
最差的情况下空间复杂度为:O( N ) ;退化为冒泡排序的情况
⛅时间复杂度:
快速排序最优的情况下时间复杂度为:O( NlogN )
快速排序最差的情况下时间复杂度为:O( N^2 )
快速排序的平均时间复杂度也是:O(NlogN)
快速排序稳定性
快速排序显然是不稳定的,我们试想一下:5 ….5…1….5,这种情况,交换第一个5和1的时候,显然三个5的前后顺序发生了变化,是不稳定的
归并排序
递归版本
🐾 基本思想:(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
🌴归并条件: 左区间有序 右区间有序
🔥同样的我们看图说话!
上半部分递归树为将当前长度为 n 的序列拆分成长度为 n/2 的子序列,下半部分递归树为合并已经排序的子序列
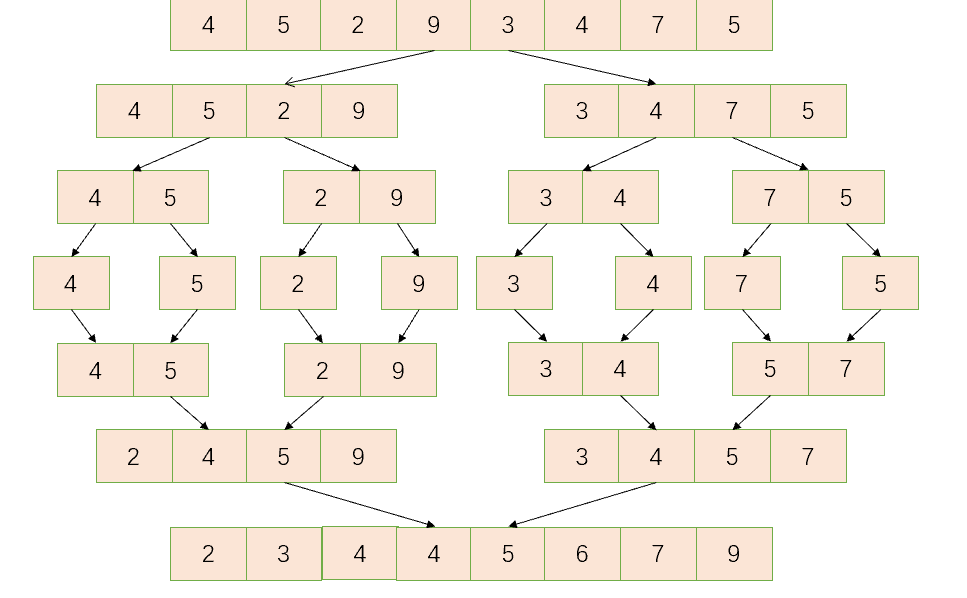
再来一张动态图应该更好理解吧~
归并排序代码实现:
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
return;
int mid = left + (right - left) / 2;
// 归并条件:左区间有序 右区间有序
// 如何做到?递归左右区间
// [left, mid] [mid + 1, right]
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
//归并
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;
//对归并的数组进行排序,暂存到tmp数组中
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//两个while循环将两个归并数组未加入tmp中的元素加入到tmp当中
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//将tmp数组的值赋值给数组a,因为a是指针,所以对形参进行修改对应实参也会修改
for (i = left; i <= right; i++)
{
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
归并排序时间复杂度和空间复杂度
⛅时间复杂度:O(N*logN)
⛅空间复杂度: O(N),要来一个临时空间存放归并好的区间的数据
归并排序稳定性
归并排序在遇到相同的数时,可以就先将放前一段区间的数,再放后一段区间的数就可以保持稳定性了,所以说这个排序是稳定的
非递归版本
🐾 基本思想: 这里我们用循环来实现这个非递归的归并排序,我们可以先两两一组,在四个四个一组归并……
🔥同样的我们看图说话!(分两种情况讨论)
特殊情况(元素个数为2^i)
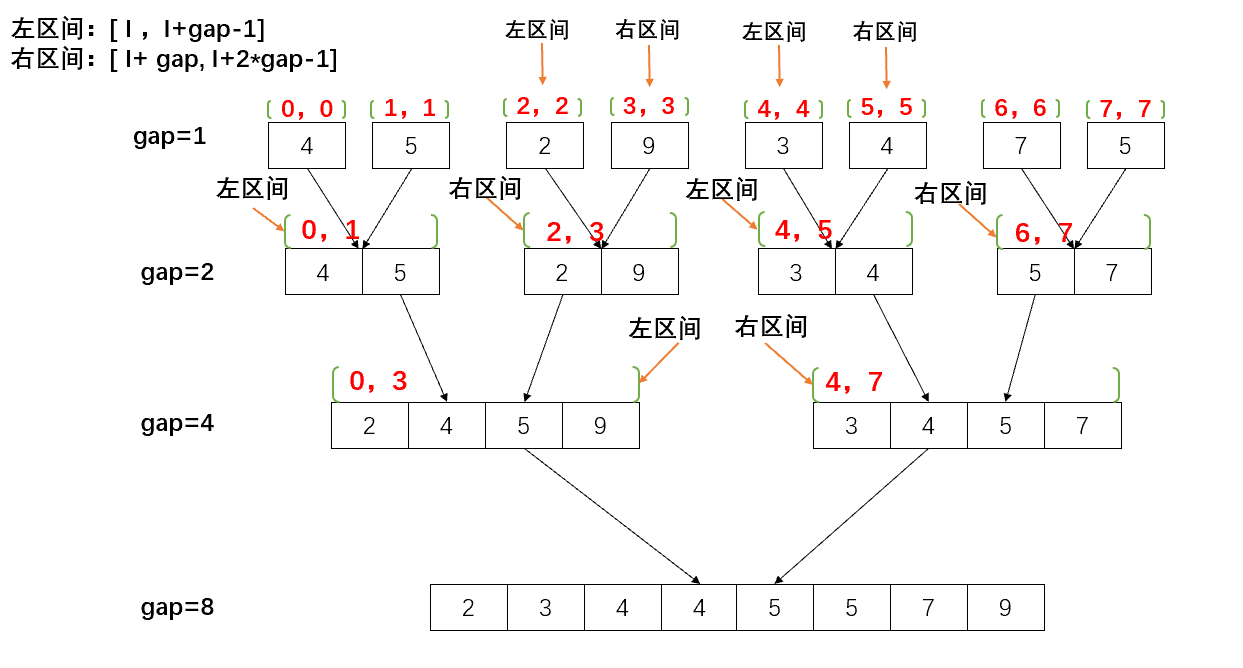
根据上面这个图,我们可以很快的写出一个框架,例如下面的代码:
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;//每趟合并后序列的长度
while (gap < n)//合并趟数的结束条件是:最后合并后的序列长度>=数组元素的个数
{
int i = 0;
//每趟进行两两合并
for (i = 0; i < n; i += 2 * gap)
{
// [i, i+gap-1] [i+gap, i+2*gap-1]
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
int j = 0;
for (j = i; j <= end2; j++)
{
a[j] = tmp[j];
}
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
一般情形(数组的元素个数不一定是2^i )
虽然元素个数不一定是 2^i 个,但是任意元素的个数为n,都必然可以拆写成 2^j+m 个元素的情况
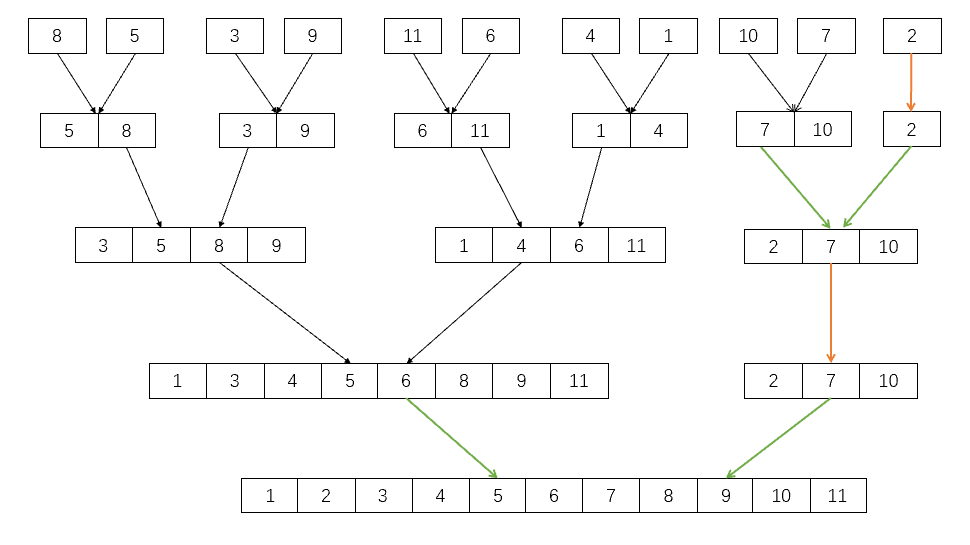
由图可知,这种情况下存在两种特殊情况:
- 橙色箭头代表无需合并,因为找不到配对的元素,造成该情况的原因是归并过程中,右半区间不存在,此时我们可以不进行这次归并,直接跳出循环,也就是begin2>=n的时候,我们就break跳出这次循环,不进行归并
- 绿色箭头代表两个长度不相等的元素也要合并,归并过程中,左区间存在,右区间也存在,但是右区间和左区间长度不一样,就意味着end2>=n的情况,此时我们只需要对end2进行调整,使得右区间范围缩小,不越界,就可以继续归并
我们可以看到这种情况在一次归并中仅存在一次或者零次。
所以调整后的代码如下:
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
int i = 0;
for (i = 0; i < n; i += 2 * gap)
{
// [i, i+gap-1] [i+gap, i+2*gap-1]
// 两种需要调整的情况:
// 1.右区间不存在
// 2.正要归并的右区间和左区间长度不一样
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
int index = i;
// 情况1:当右区间不存在的时候,右区间的范围是[begin2,end2],所以begin2越界,就代表着右区间不存在的情况
if (begin2 >= n)
break;
// 情况2,左右区间长度不一,同样此时右区间是存在的,但是end2越界,就代表了左右区间长度不一的情况,此时我们需要做调整
//将end2的长度设置成n-1,将原来的end2(越界)设置成数组a的最后一个元素的位置,因为不平衡的区间最后一个元素一定是数组a的最后一个元素
if (end2 >= n)
end2 = n - 1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
int j = 0;
for (j = i; j <= end2; j++)
{
a[j] = tmp[j];
}
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
🌾这样非递归的归并排序就这样被我们实现了。非递归归并排序的实现的难点不在框架,而在边界控制,我们要把边界控制的到位,这样就能够很好地实现这个非递归
计数排序
🐾 基本思想: 它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 当然这是一种牺牲空间换取时间的做法
🔥同样的我们看图说话!
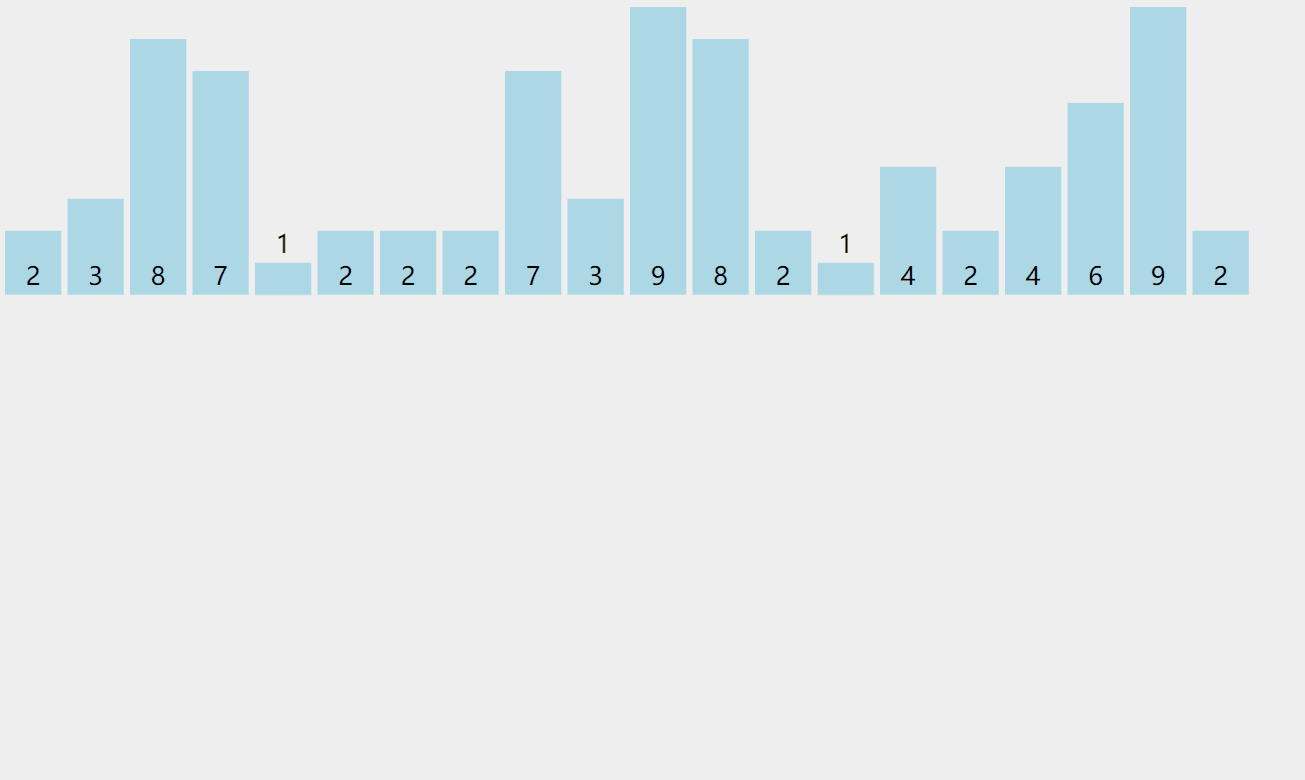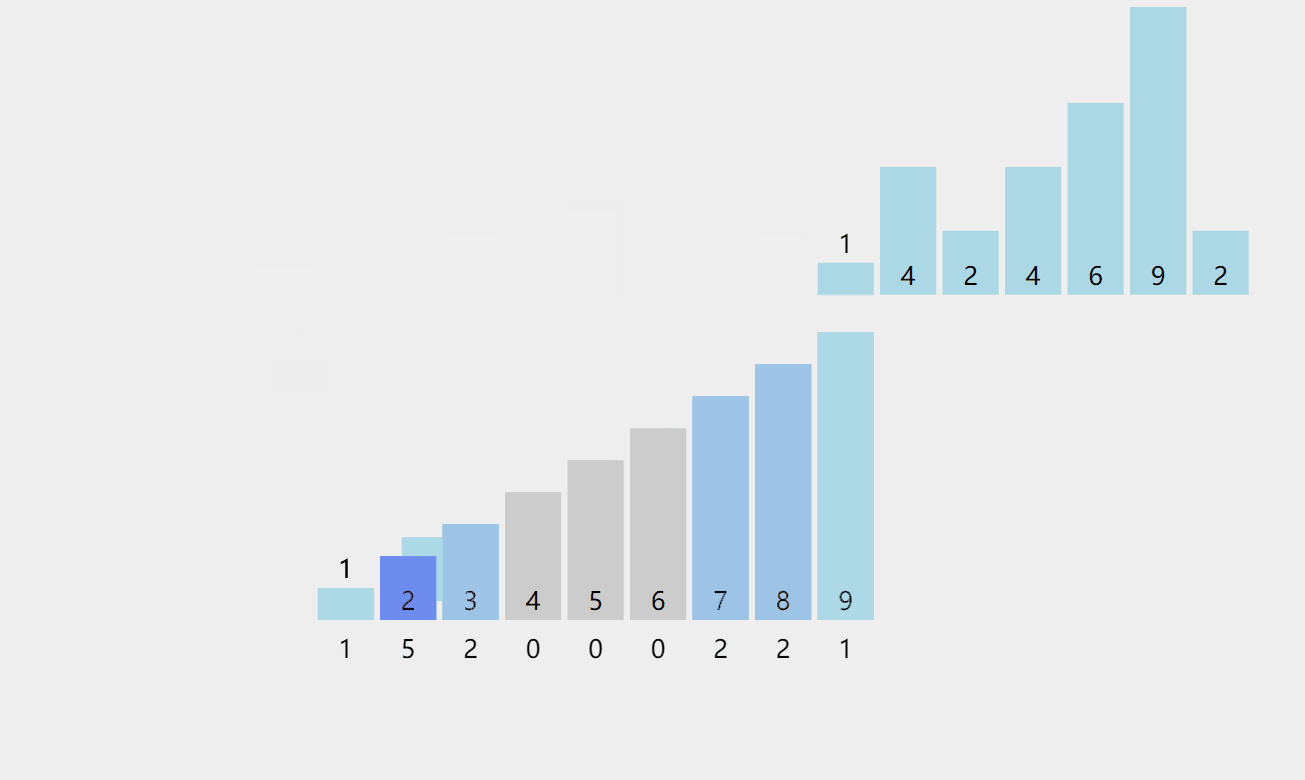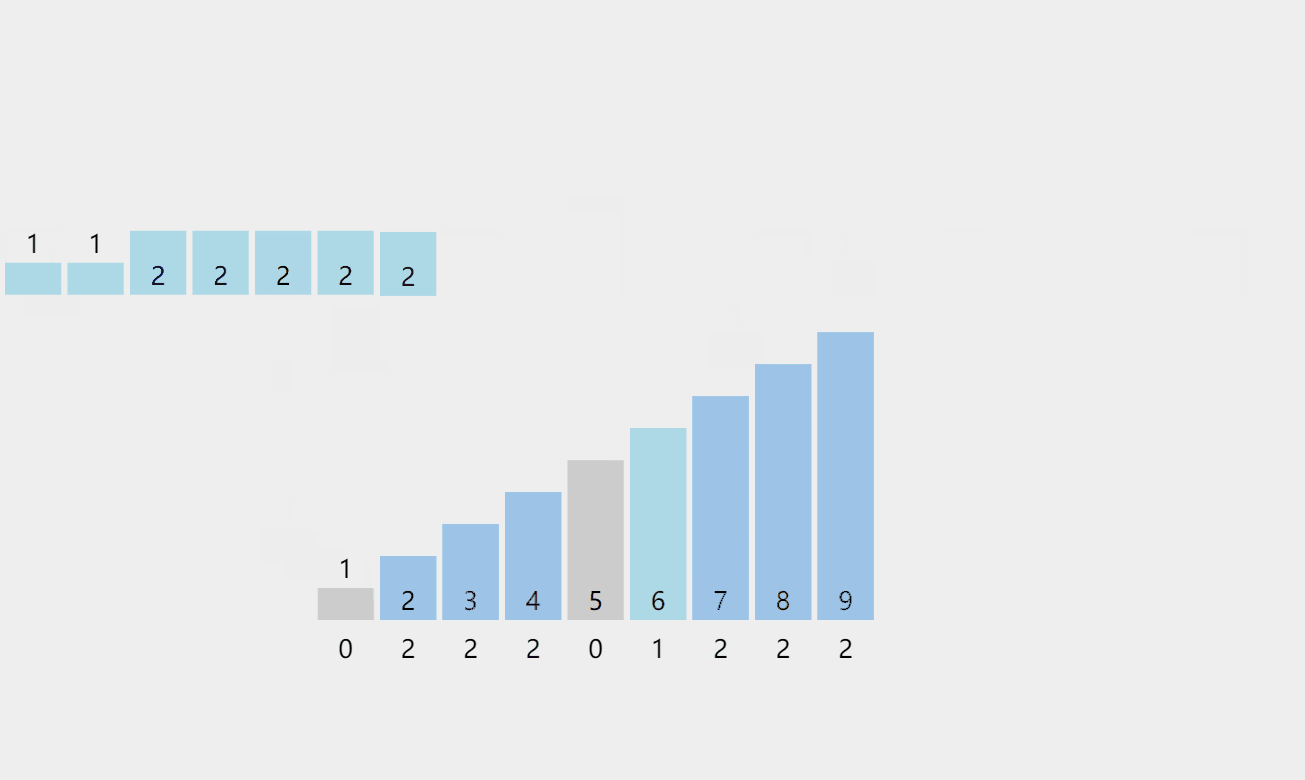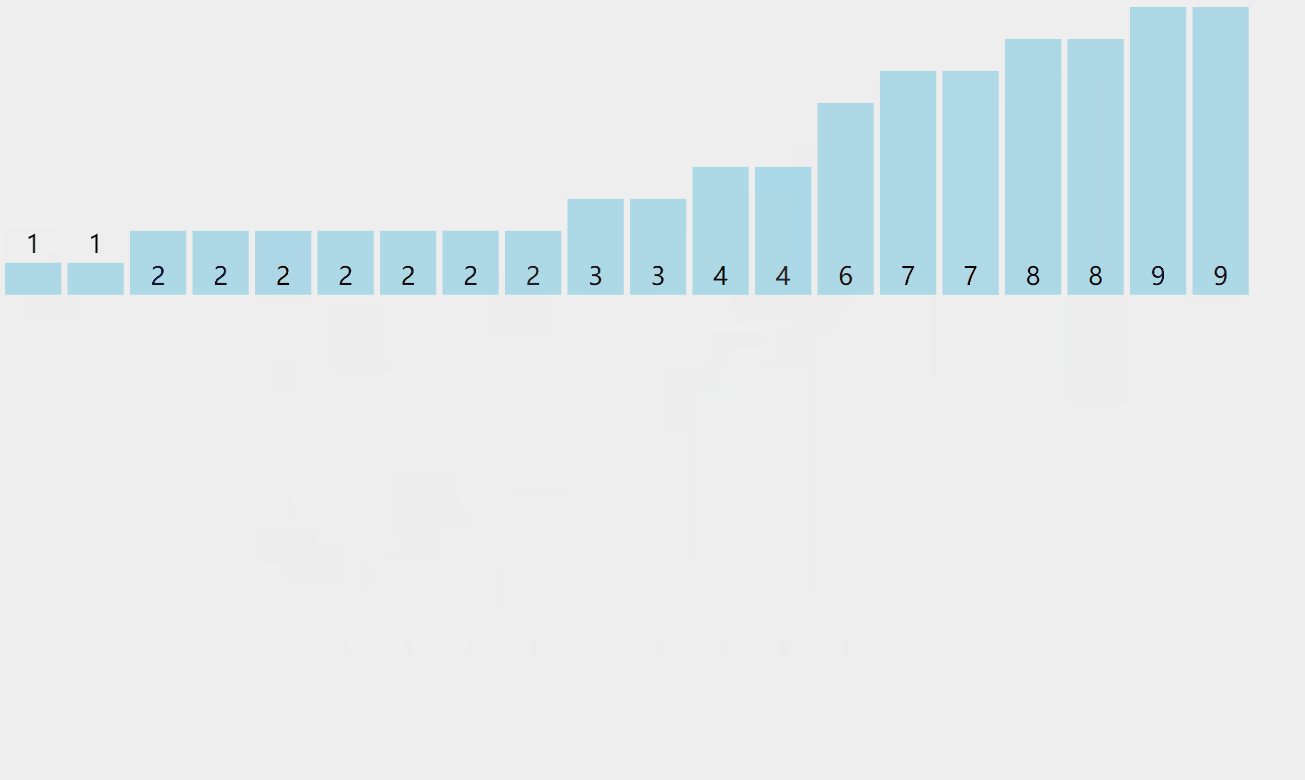
我们可以先计数出这个序列数据的范围也就是range = max – min + 1,最大值和最小值都可以通过遍历一遍序列来选出这两个数。然后我们可以开一个大小为range的计数的空间count中,然后将序列中的每一个数都减去min,然后映射到count这个空间中,然后我们再一次取出并加上min依次放进原数组空间中,这样我们就顺利地完成了排序
具体代码实现如下:
void CountSort(int* a, int n)
{
int min = a[0];
int max = a[0];
int i = 0;
for (i = 1; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
printf("malloc error\n");
exit(-1);
}
// 初始化开辟的空间
memset(count, 0, sizeof(int) * range);
for (i = 0; i < n; i++)
{
count[a[i] - min]++;
}
int index = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[index++] = i + min;
}
}
free(count);
count = NULL;
}
计数排序时间复杂度和空间复杂度
⛅空间复杂度: O(N),要来一个临时空间存放归并好的区间的数据
⛅时间复杂度:O(MAX(N,范围))(以空间换时间)
计数排序稳定性
计数排序在我们这个实现里是不稳定的
排序比较
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(nlogn~n^2) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 直接选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |