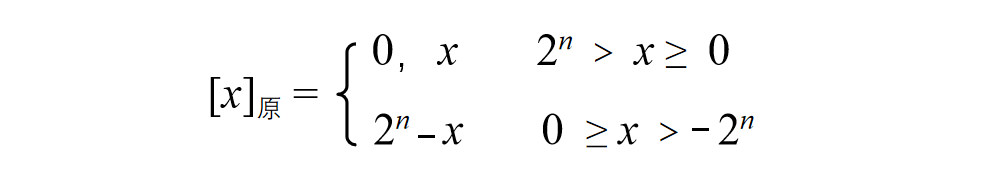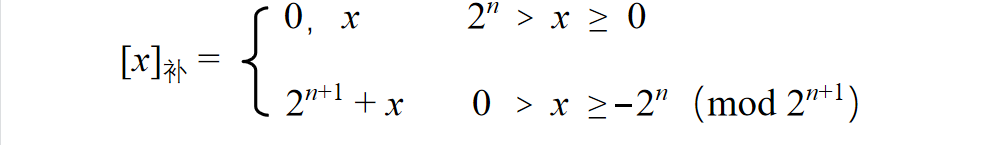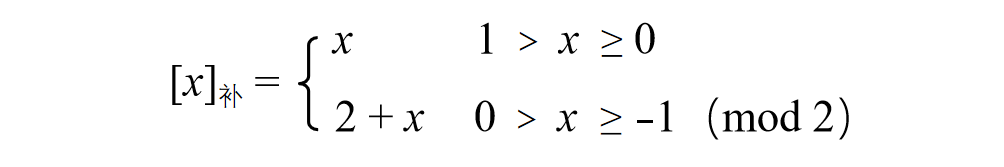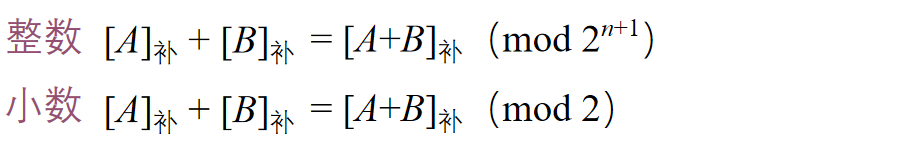【计算机组成原理】第6章 计算机的运算方法
教材基于《计算机组成原理 第3版》 ——唐朔飞
无符号数和有符号数
无符号数
无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
寄存器的位数用来反映无符号数的范围。

有符号数
原码
🌅 原码的定义:
-
整数
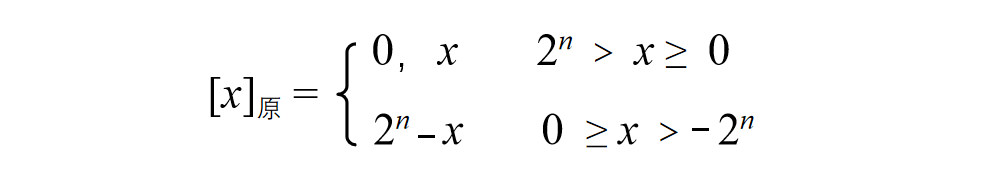
-
小数

🌰 举例:




反码
🌅 反码的定义:
-
整数

-
小数


补码
🌅 补码的定义
-
整数
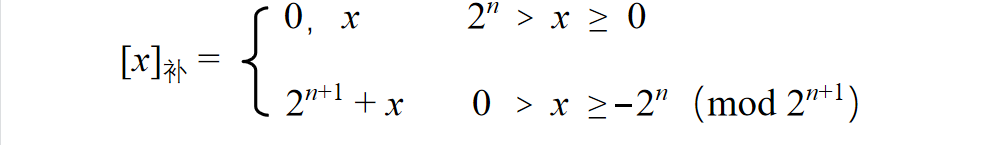
-
小数
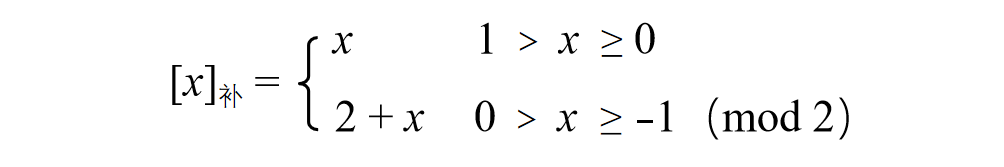

🔔 当真值为 负 时,原码 可用 补码除符号位外 每位取反,末位加 1 求得
⚠️ 求补码的另一种方法:从原码的最右端开始向左数,数到第一个 1 停止,该位置左边的所以位数(除了符号位)取反。

1️⃣ 一个负数加上 “模” 即得该负数的补数
2️⃣ 一个正数和一个负数互为补数时,它们绝对值之和即为模数
🌰 举例:

移码
🌅 移码的定义


🔔 最小真值的移码为全 0

练习

三种机器数的小结
1️⃣ 最高位为符号位,书写上用“,”(整数)或“.”(小数)将数值部分和符号位隔开
2️⃣ 对于正数,原码 = 补码 = 反码
3️⃣ 对于负数 ,符号位为 1,其数值部分
- 原码除符号位外每位取反末位加 1 -> 补码。
- 原码除符号位外每位取反 -> 反码

- 原码和反码的真值 0 有两种表示
- 补码和移码的真值 0 只有一种表示
- 补码和移码可以多表示一个负数
数的定点表示和浮点表示
定点表示

浮点表示
浮点数的表示形式


浮点数的表示范围


IEEE 754 标准




定点运算
移位运算
🌈 算术移位规则



🌈 算术移位和逻辑移位的区别

加减法运算
补码加减运算公式
-
加法
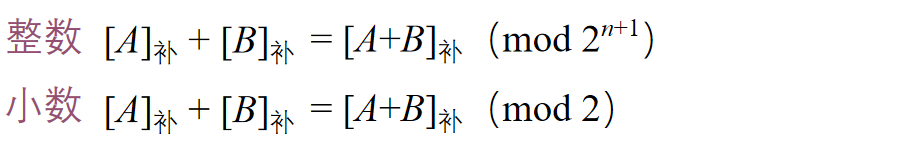
-
减法
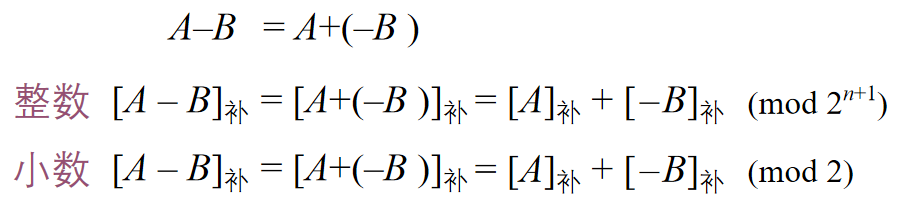
-
连同符号位一起相加,符号位产生的进位自然丢掉

-
溢出判断
-
一位符号位判溢出:参加操作的 两个数(减法时即为被减数和“求补”以后的减数)符号相同,其结果的符号与原操作数的符号不同,即为溢出
-
两位符号位判溢出:结果的双符号位 相同:未溢出;结果的双符号位 不同:溢出。最高符号位 代表其 真正的符号
-
乘法运算
原码乘法
- 原码一位乘运算规则



补码乘法
-
补码一位乘运算规则

-
Booth 算法(被乘数、乘数符号任意)
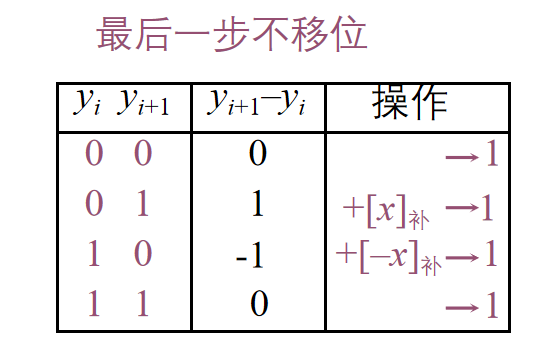
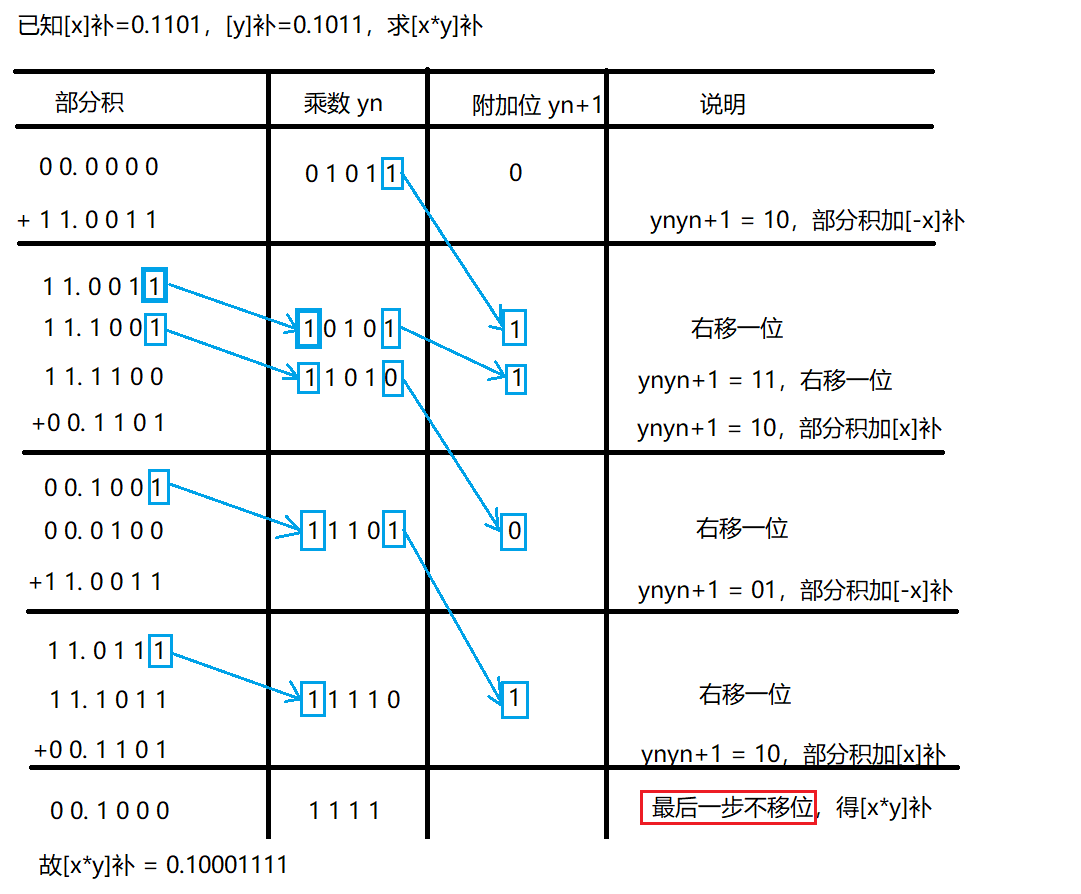
除法运算
原码除法

-
恢复余数法
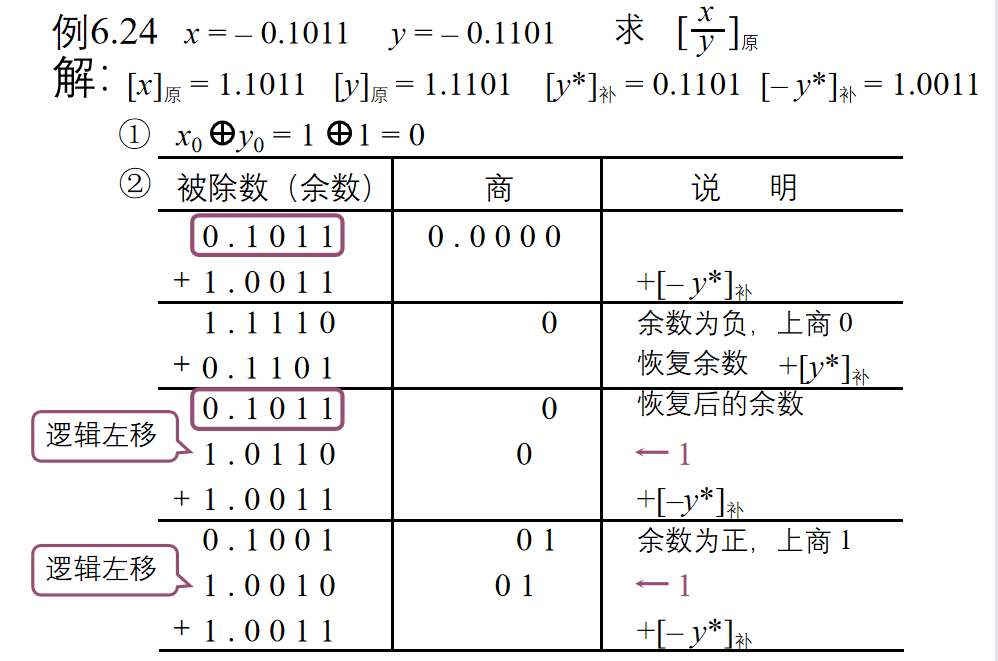
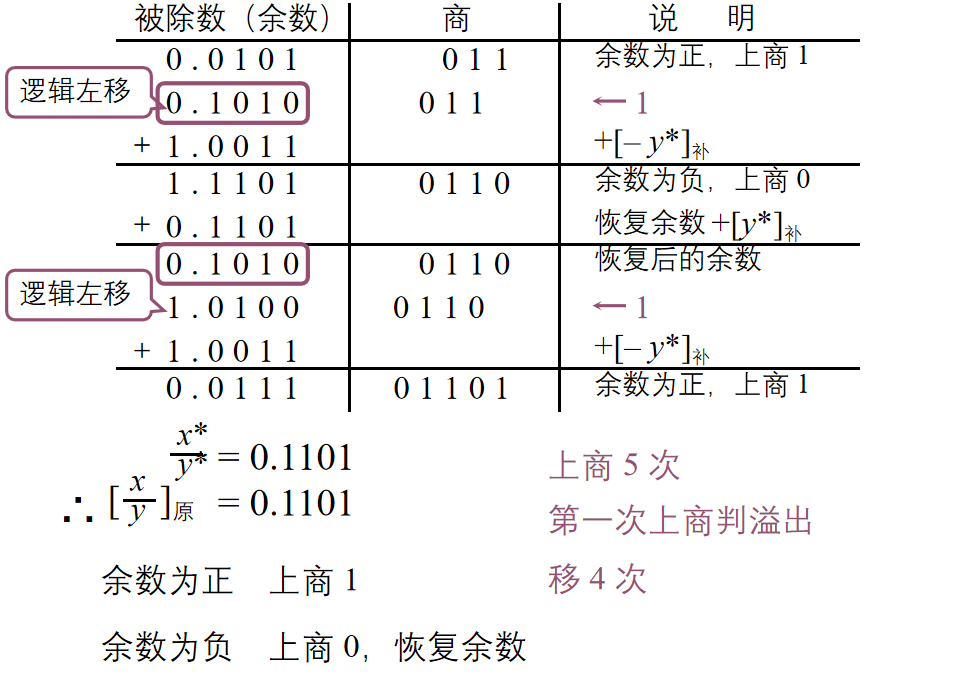
-
不恢复余数法(加减交替法)
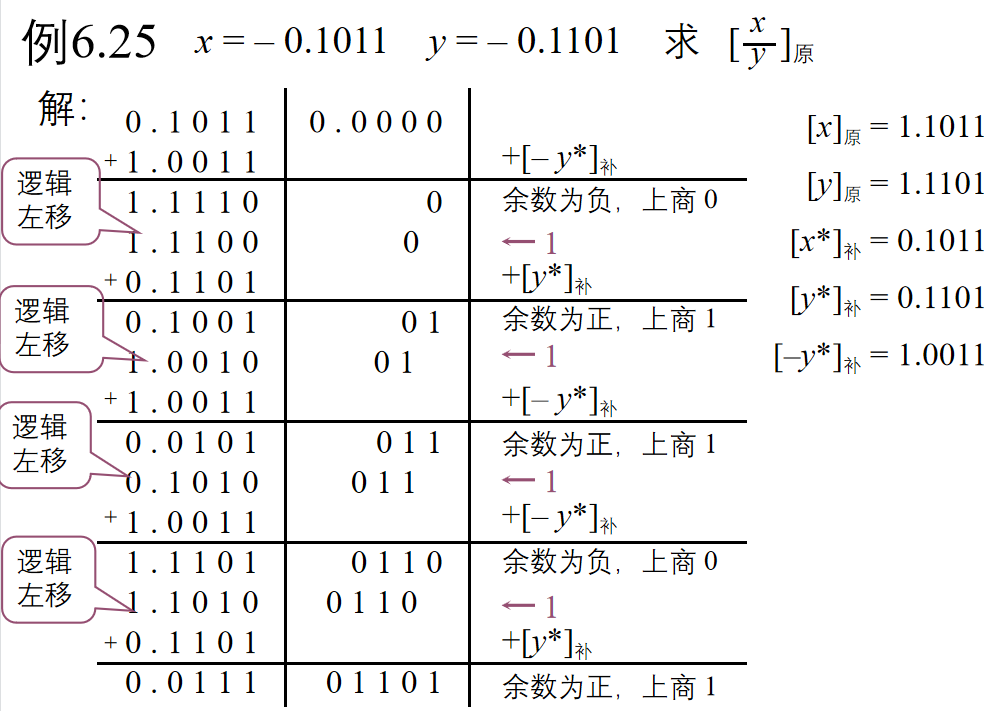

补码除法
- 余数补码与除数补码同号:上商“1”;不同号:上商“0”
- 末位商恒置“1”


补码除和原码除(加减交替法)比较