【UV统计】海量数据统计的前世今生
背景
在互联网公司中,每个项目都需要数据统计、分析,便于项目组利用详细数据研究项目的整体情况,进行下一步的调整。在数据统计中,UV统计是最常见的,也是最普遍的。有的场景要求实时性很高,有点场景要求准确性很高,有的场景比较在意计算过程中的内存。不同的场景使用不同的算法,下面我们从0到1简单介绍下UV统计领域。
什么是UV统计
假设我们的场景是商家这边上架一系列水果,然后需要统计出一共上架几种水果。具体如下所示:
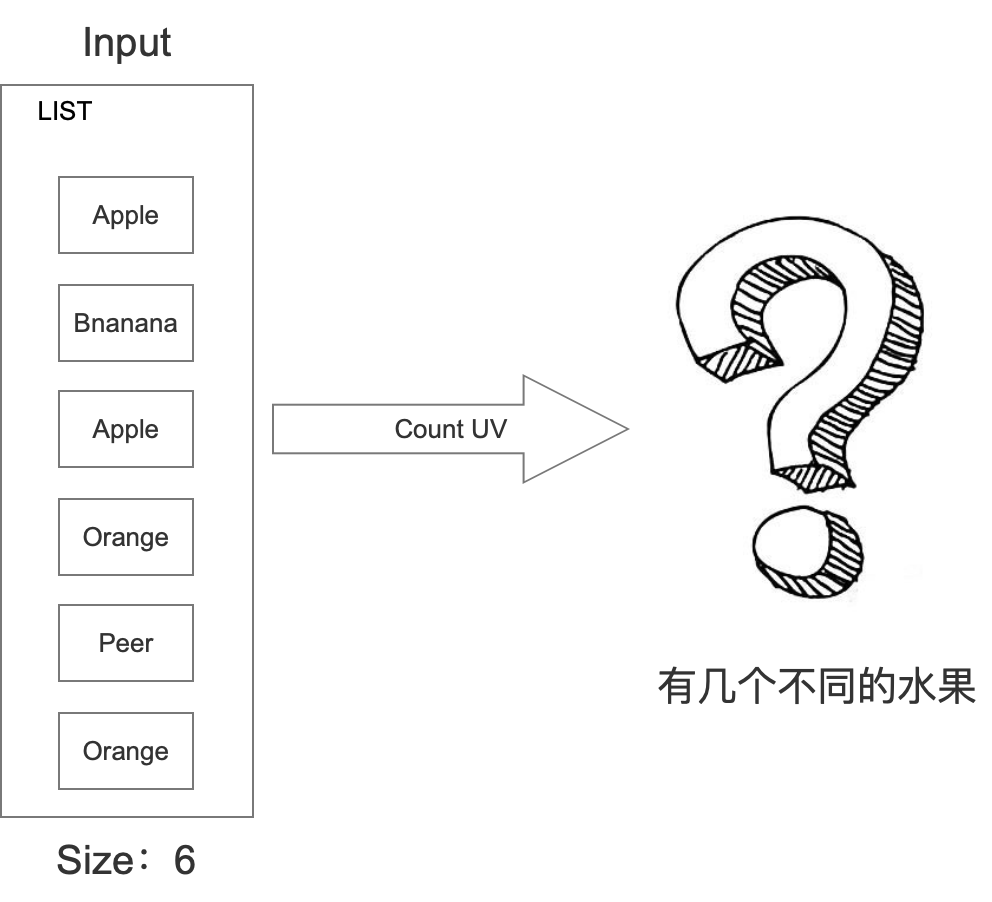
针对这个问题,我们想到的最简单的方式就是利用STL中的set处理。
SET
上架一个水果的时候,也同时在set中插入。最后需要统计的时候,直接计算set中一共有几个水果即可。具体如下所示:
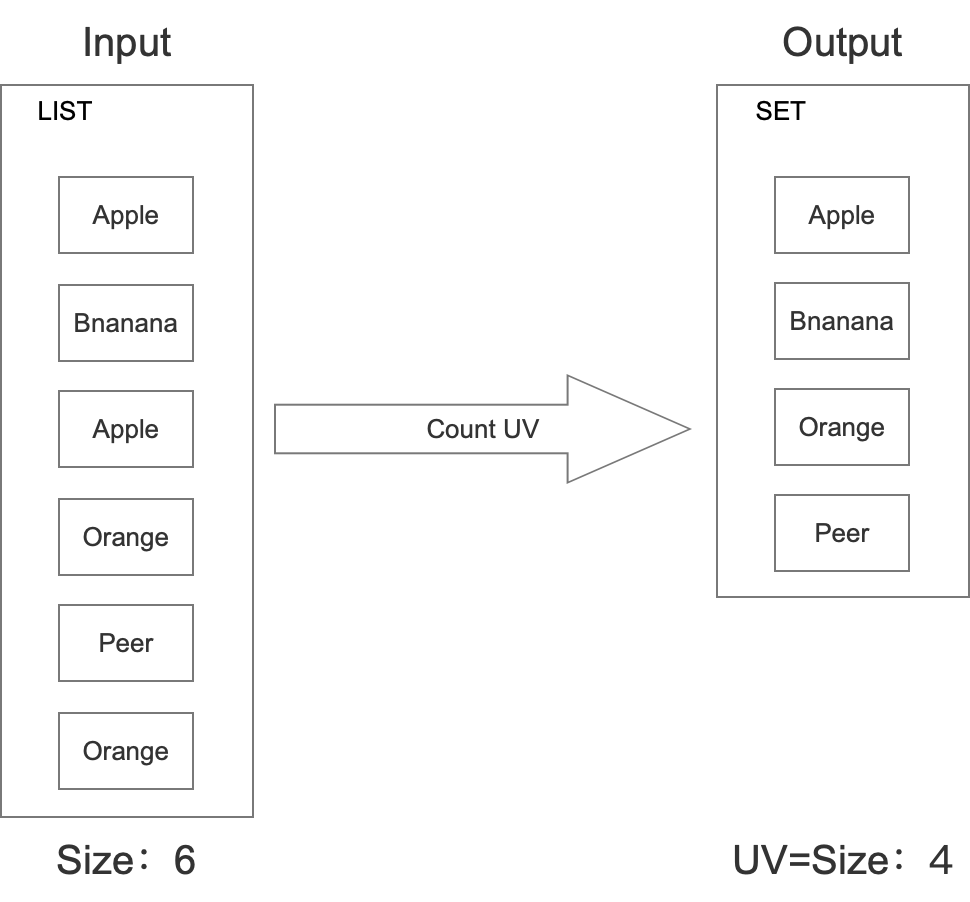
这种方式准确率是绝对准确的,但是这种方式耗费的内存是很大的。
假设每个水果需要 K 字节,那么如果有 M 个水果,一共需要 K * M 字节。那么我们能不能缩小这里的内存呢?
稍微损失一点准确率换取内存?具体见下面HashMap的方式
HASHMAP
这种算法在上架一个水果的时候,只需要在特定的位置置1即可,而不需要存储这个位置上究竟是何种水果。然后在统计的时候,只需要统计hashmap里面有多少个1即可。具体如下所示:
具体如下所示:
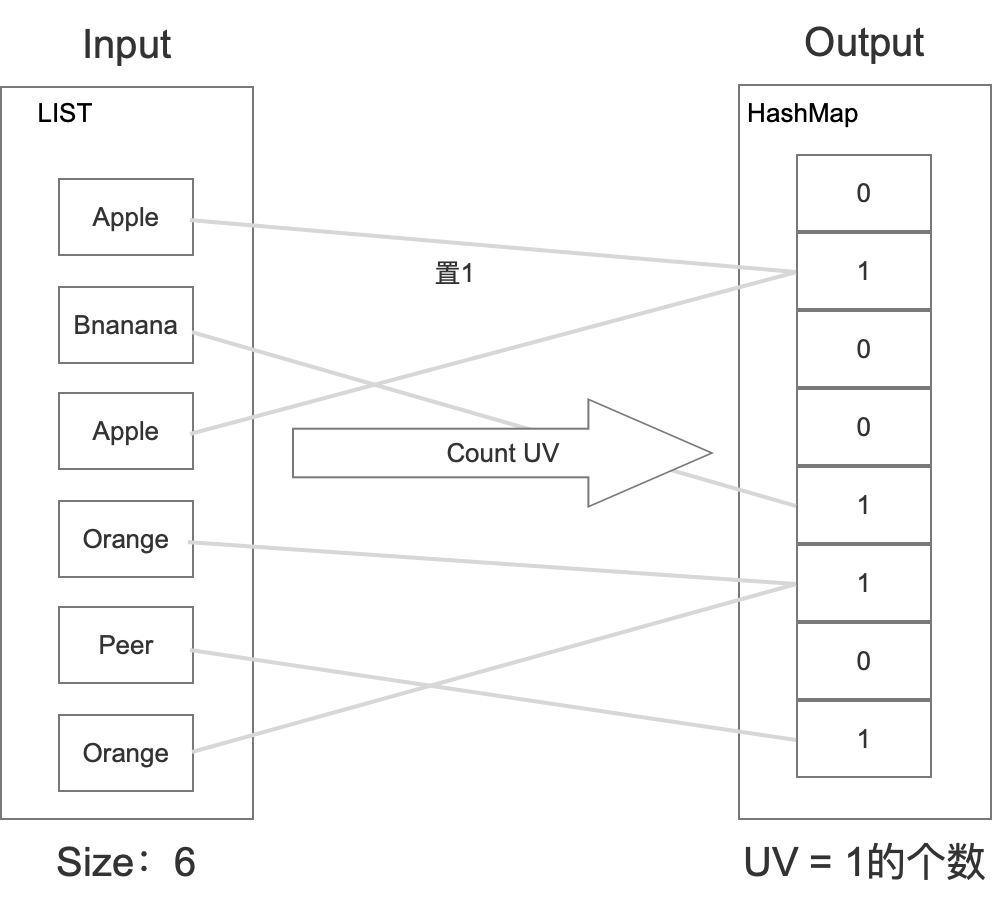
那么如果有M个水果,这里其实只需要 M / 8 字节,相比set的方式内存直接缩小到1/8。当然Hash肯定会有冲突的,所以这里肯定有一定准确率的损失。
但是如果涉及到海量数据的UV统计,这里的内存还是很大的。
能否用上统计学进一步缩小内存呢?具体见下面的Linear Count的方式。
Linear Count
这种算法在上架一个水果的时候,完全跟hashmap一致,在相应位置置1。
然后在统计的时候,利用统计学的方式,根据hashmap中零的个数给出一个估算值。具体如下所示:
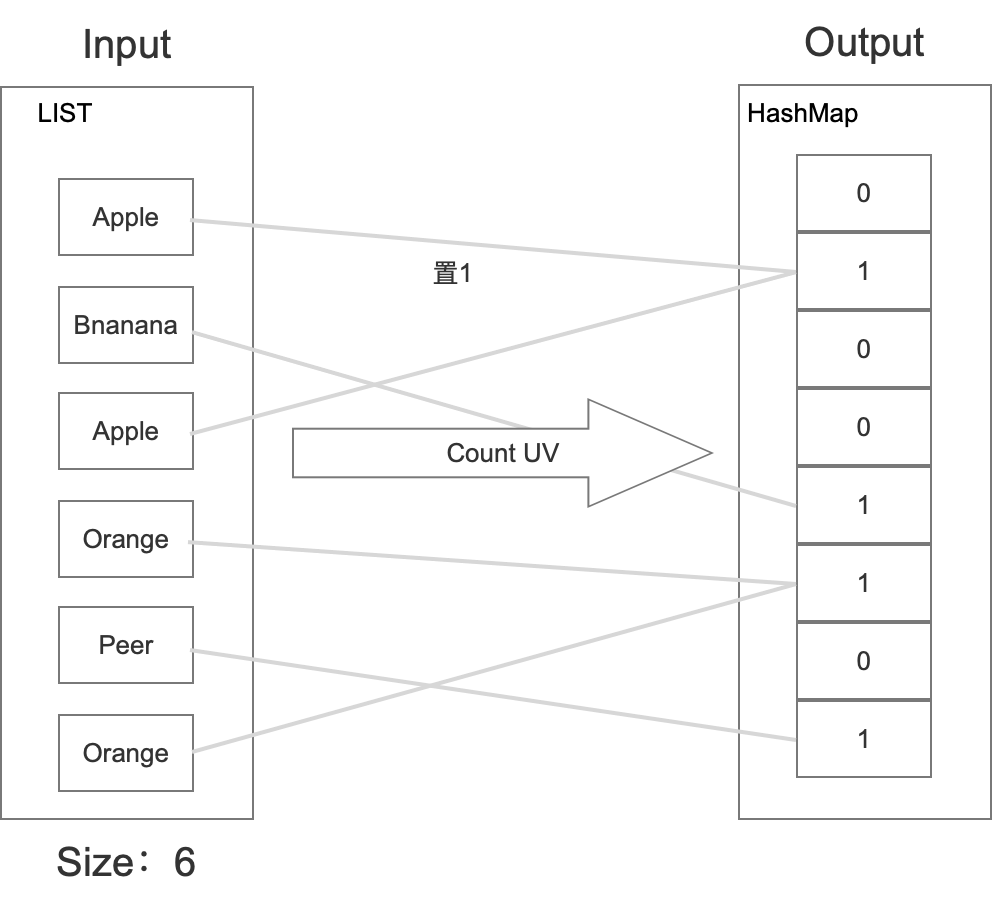
假设M为哈希桶长度,那么每次上架水果,每个桶被选中的概率为:
$$\frac{1}{M}$$
然后在上架N个元素后,某个桶为0的概率为:
$$(1-\frac{1}{M}) ^N$$
所以在上架n个元素后,哈希桶中零的个数期望为:
$$ZeroNum=\sum_{i=1}^M (1-\frac{1}{M}) ^N = M (1-\frac{1}{M}) ^N= M ((1+\frac{1}{-M}){-M}){-\frac{N}{M}}) \approx Me^{- \frac{N}{M}}$$
所以最终:
$$
N = UV = -M ln(\frac{ZeroNum}{M})
$$
所以Linear Count算法中,只需统计下hashmap中零的个数,然后代入上式即可。
这种算法在N很小的时候,准确率是很高的,但是N很大的时候,它的准确率急剧下降。
针对海量数据的情况,LogLog Count的算法更加鲁棒
LogLog Count
这种算法跟上面几种都不同,上架水果的时候,在相应桶里面记录的是二进制数后面最长的连续零个数。然后统计的时候,利用统计学的方式,根据存储中最长连续后缀零个数,得出一个估计值。具体如下所示:
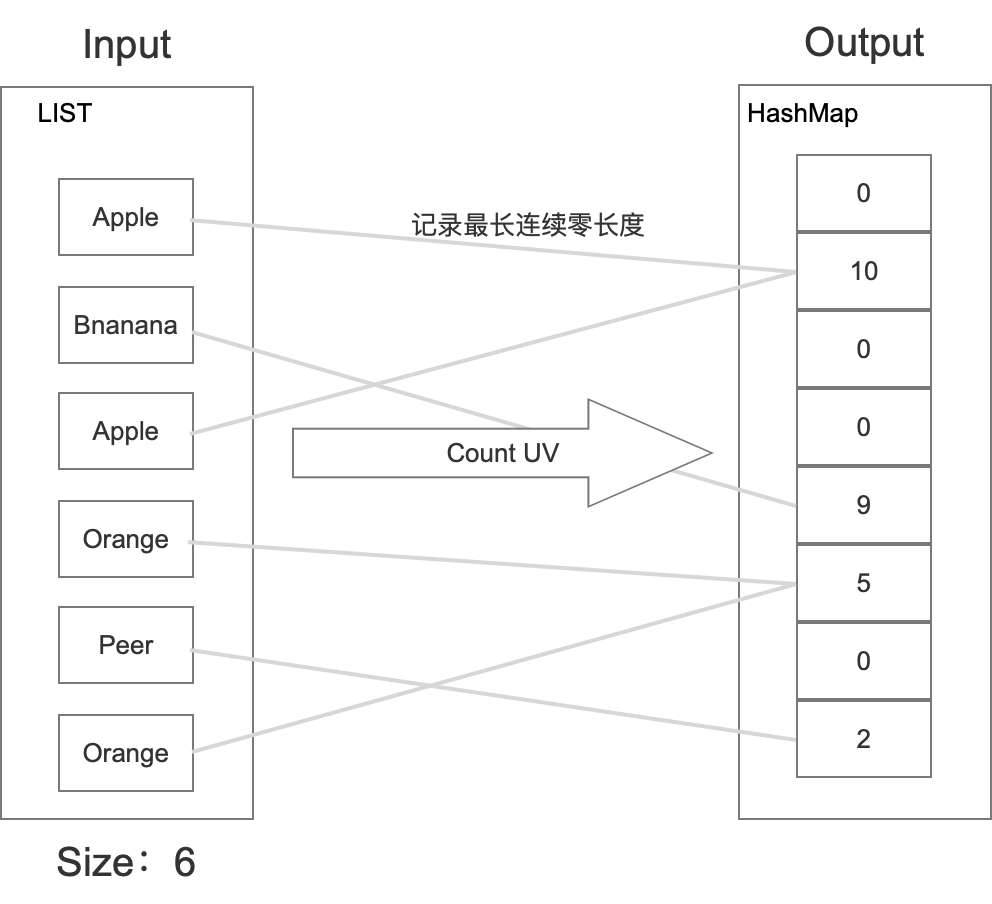
它的原理如下:


这里如果只使用一个桶来估计的话,它的误差是很大,需要用分桶平均的方式来减少它的误差。
分桶平均
既然这里利用了分桶来减少误差,那么这里统计的时候就必须合起来,这里有4种方式:
- 算术平均:$$UV=\frac{\sum_{j=1}^mUV_j} { m}$$
- 几何平均:$$UV=\sqrt[m]{UV_1…UVm}$$
- 调和平均:$$UV=\frac{m}{\sum_{j=1}mUV_j{-1}}$$
- 中位数:$$UV=mediam {UV_1,…,UV_m}$$
LogLog Count利用的是算术平均的方式,所以最终估计值为:
$$UV=2{\frac{\sum_{j=1}m{UV_j}}{m}}$$
这种算法对于基数大的情况下准确率挺高的,但是基数小的情况下准确率很低。
HyperLogLog Count
这种算法跟LogLog Count 类似,有个区别点就是它在求均值的时候利用了调和平均数,而不是算术平均数。这里最终估计值为:
$$UV=mm(\sum_{j=1}m{2{-M_j}})^{-1}$$
然后它还引入了分段误差修正。
误差修正

具体可以看我github上的代码:HyperLogLog
总结
| 准确率 | 内存 | 耗时 | |
|---|---|---|---|
| Set | 绝对准确 | K * M | O(Mlog(M)) |
| HashMap | 很高 | M/8 | O(M) |
| Linear Count | 基数小高,基数大低 | M/8 | O(M/8) |
| LogLog Count | 基数小低,基数大高 | ||
| HyperLogLog Count | 高 |


