算法 | 归并排序
- 2020 年 4 月 30 日
- 筆記
归并排序
归并排序算法的核心就是 “归并”,将两个有序的数列合并,形成更大的有序数组。
归并排序的原理
上面说了,归并排序的核心就是“归并”。如果排序一个数组,那么将数组从中间分成前后两部分,对前后两部分分别进行排序,然后再将排序好的合并在一起,那么这样整个数组就会成为更大的有序数组。例如下面示图:
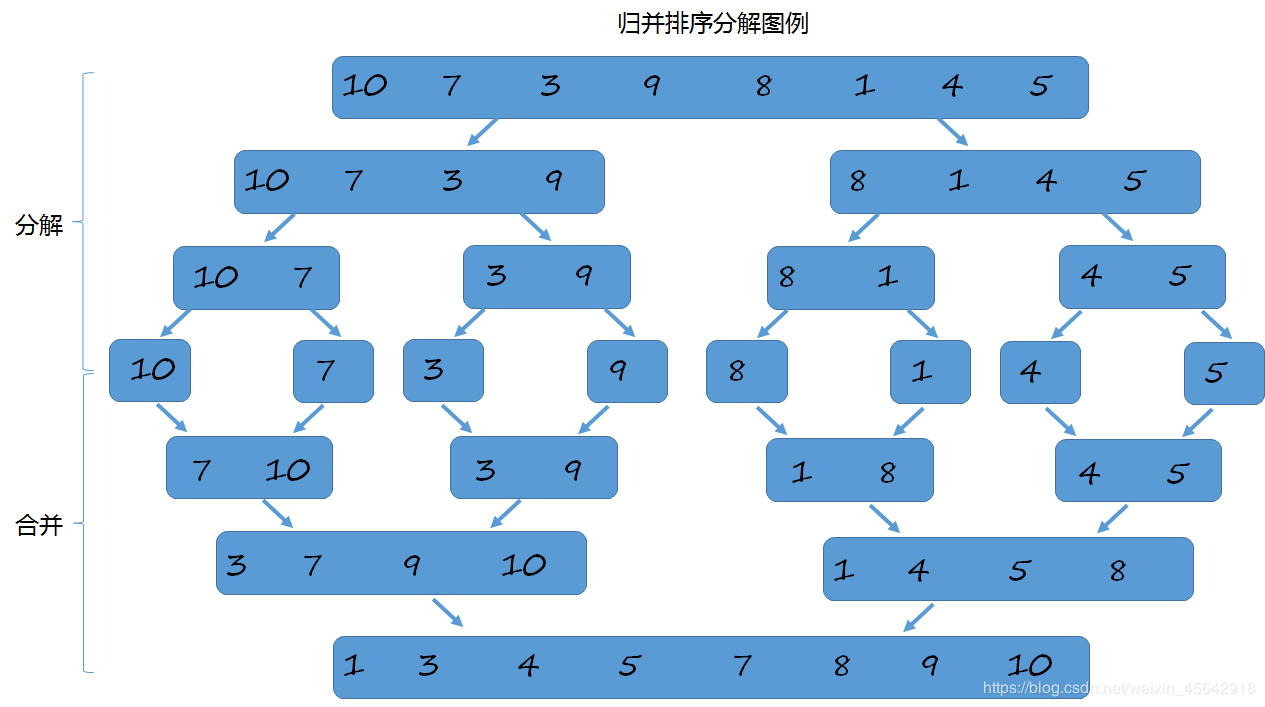
归并排序使用的思想是分治思想,即是分而治之。将复杂问题分解成两个或者多个规模相同或类似的子问题,然后继续细化,当子问题足够简单,能够被求解,那么复杂的问题也就能够被求解出来。
这里跟递归的思想很像。递归也是将大问题细化为小问题,找出终止条件和递推公式。分治算法一般都是用递归实现的。分治的思想是一种解决问题的处理思想,递归是一种编程技巧,两者不会冲突。
上面说了,归并排序能够使用递归实现,那么现在先写出递推公式和终止条件。
# 递推公式
merge_sort(a...b) = merge(merge_sort(a...k), merge_sort(k+1, b))
# 终止条件
a >= b,不再继续分解
这里解释下上面的公式,终止条件不细讲,这里表示的,索引 a 大于等于 索引 b,即是已经到达数组末尾,不能够再细分。
讲下递推公式,merge_sort(a...b),表示给索引 a 到 k 之间的数组进行排序。这里将分体转为为两个子问题,merge_sort(a...k) 和 merge_sort(k+1...b),其中 k 表示原数组中间的位置。而 merge() 函数表示当两个将两个排好序的子数组合并,这样就能够使原数组实现排序。
现在将这个递推公式转化为代码(这里使用伪代码):
# nums 表示数组,a 为起始点,b 为数组末尾索引
def merge_sort(nums, a, b):
# 终止条件
if a >= b:
return
# 取中间位置
k = (a + b) // 2
# 分治递归
merge_sort(nums, a, k)
merge_sort(nums, k+1, b)
merge(nums[a...b], nums[a...k], nums[k+1, b])
最后 merge() 函数的作用,就是将后面两个子数组合并好后放到 nums[a…b] 中。现在主要的问题是如何实现分解后排序合并?
先用一个简单的示例,如下示图:

先申请临时数组 temp,定义指针 i,j 分别指向 两个子数组的第一个元素。比较 nums[i],nums[j],较小的元素放入临时数组中,同时该元素的指针向右移动。
循环上面的过程,直到其中一个子数组的所有数据都放入临时数组中,这个时候,将另外一个数组剩下的部分也放到临时数组中。这个临时数组就是最终合并的结果,将其复制回原数组即可。
现在用伪代码实现这个过程:
def merge(nums[a...b], nums[a...k], nums[k+1, b]):
# length 表示数组大小
temp = [0] * length
# 初始化指针,i, j, ti
i, j, ti, = a, k+1, 0
# 取小值放入临时数组中,
while (i <= k and j <= b):
if (nums[i]<=nums[j]):
temp[ti]=nums[i]
i+=1
else:
temp[ti]=nums[j]
j+=1
ti+=1
# 合并时会出现一个数组全部放入临时数组中,
# 另外一个数组还有剩余,这里将剩余部分也放到临时数组中
if i < nums[a...k].length:
for x in range(i, nums[a...k].length):
temp[ti] = nums[x]
ti += 1
else:
for x in range(j, nums[k+1...b].length):
temp[ti] = nums[x]
ti += 1
# 如果需要复制回原数组,也可以直接复制
return temp
以上本篇幅就是关于归并排序的主要内容。
欢迎关注微信公众号《书所集录》


