动态规划-最长上升子序列模型
1. 题目描述
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数N。
第二行包含N个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
\(1≤N≤1000\),
\(−10^9≤数列中的数≤10^9\)
输入样例:
7
3 1 2 1 8 5 6
输出样例:
4
2. (DP)朴素解法\(O(n^2)\)
本题是一个简单的DP问题。
令\(a[i]\)表示数组中第\(i\)个数,\(f[i]\)表示以数组中第\(i\)个数结尾的最长上升子序列的长度。
则\(f[i] = max(f[j]) + 1,j < i 且a[j] < a[i]\)
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N], a[N];
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
int res = 0;
for(int i = 1; i <= n; i ++)
{
// 注意初始化f[i] = 1.
f[i] = 1;
for(int j = 1; j < i ; j ++)
if(a[j] < a[i])
f[i] = max(f[i],f[j] + 1);
res = max(res, f[i]);
}
cout << res << endl;
return 0;
}
3. (DP+贪心)优化版本\(O(nlgn)\)
通过对本题的观察与思考。我们可以得到如下的事实:
- 对于两个长度相同的子序列,假设两个子序列的最后一个值分别是\(x_1, x_2\),且\(x_1 > x_2\)。假设我们的\(a[i]\)可以放在最后一个值为\(x_1\)的序列的后面,则其一定能够放在最后一个值为\(x_2\)的序列的后面。故,对于长度相同的序列,我们只需要存储最后一个值小的序列即可。
当我们扫描到第\(i\)个数的时候,可以将其前面的数构成的子序列按长度进行分类,长度为\(1\)的最长上升子序列只存储结尾值最小的,长度为\(2\)的最长上升子序列只存储结尾值最小的,那么我们可以证明:不同长度最长上升子序列最后一个数的值是随长度严格单调递增的。
证明:
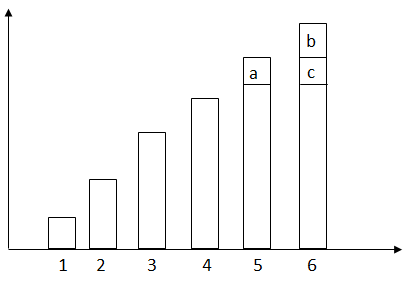
假设长度为\(5\)的最长上升子序列最后一个数为\(a\),长度为\(6\)的最长上升子序列最后一个数为\(b\),倒数第二个数为\(c\)。
反证法:如果\(a>=b\),由于\(b > c\),则\(a>c\)。又由于对于长度相同的子序列我们只存储最后一个数值较小值。故\(a< c\)。推出矛盾。
这样的话,当我们扫描到第\(i\)个数的时候,就可以通过二分法,找到小于\(a[i]\),且最后一个数最大的子序列,将其该数添加到子序列后面。
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N];
int q[N];
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)cin >> a[i];
int len = 0;
q[0] = -2e9;
for(int i = 0; i < n; i ++)
{
int l = 0, r =len ;
while(l < r) // 二分法找出小于等于a[i]的最大的子序列。
{
int mid = l + r + 1 >> 1;
if(q[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1); // 更新长度
q[r + 1] = a[i]; // 更新末尾值
}
cout << len << endl;
return 0;
}
注:代码中含有部分细节没有详细说明,供读者思考
