算法学习笔记：最近公共祖先（LCA问题）

当我们处理树上点与点关系的问题时（例如，最简单的，树上两点的距离），常常需要获知树上两点的最近公共祖先（Lowest Common Ancestor，LCA）。如下图所示：

2号点是7号点和9号点的最近公共祖先

我们先来讨论朴素的做法。

首先进行一趟dfs，求出每个点的深度：

int dep[MAXN];
bool vis[MAXN];
void dfs(int cur, int fath = 0)
{
    if (vis[cur])
        return;
    vis[cur] = true;
    dep[cur] = dep[fath] + 1; // 每个点的深度等于父节点的深度+1
    for (int eg = head[cur]; eg != 0; eg = edges[eg].next)
        dfs(edges[eg].to, cur);
}

现在A点的深度比B点深，所以我们先让B点往上“爬”，爬到与A点深度相等为止。然后A点和B点再一起往上爬，直到两点相遇，那一点即为LCA：

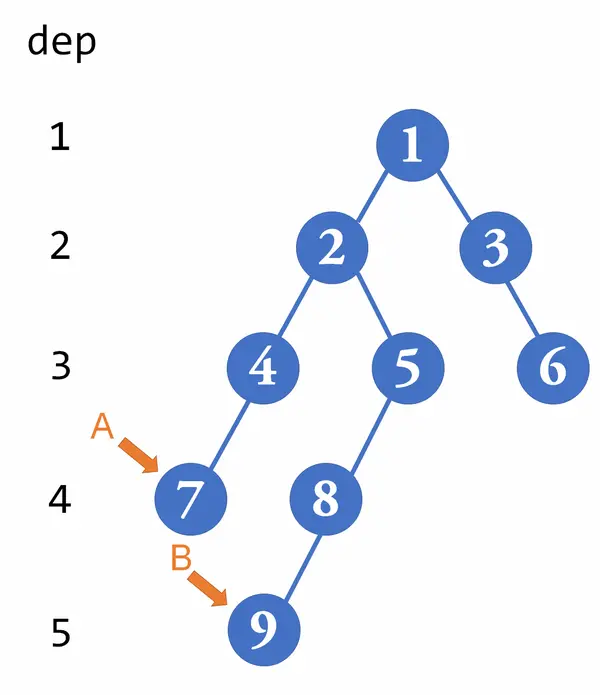
这样下来，每次查询LCA的最坏时间复杂度是 $O(n)$ 的。

有时候，我们需要进行很多次查询，这时朴素的 $O(n)$ 复杂度就不够用了。我们考虑空间换时间的倍增算法。

倍增的思想直观体现就在 ST表中提及过。我们用一个数组fa[i][k]存储 $i$ 号点的 $2^k$ 级祖先。（父节点为1级祖先，祖父结点为2级祖先……以此类推）

那么这可以在dfs途中动态规划得出：

// 在dfs中...
fa[cur][0] = fath;
for (int i = 1; i <= Log2[dep[cur]]; ++i) // Log2的预处理参见ST表的笔记
    fa[cur][i] = fa[fa[cur][i - 1]][i - 1]; // 这个DP也参见ST表的笔记

这样，往上爬的次数可以被大大缩短（现在变成“跳”了）。

首先还是先让两点深度相等：

if (dep[a] > dep[b]) // 不妨设a的深度小于等于b
    swap(a, b);
while (dep[a] != dep[b]) // 跳到深度相等为止
    b = fa[b][Log2[dep[b] - dep[a]]]; // b不断往上跳

例如，a和b本来相差22的深度，现在b不用往上爬22次，只需要依次跳16、4、2个单位，3次便能达到与a相同的距离。

两者深度相等后，如果两个点已经相遇，那么问题就得以解决。如果尚未相遇，我们再让它们一起往上跳。问题在于，如何确定每次要跳多少？正面解决也许不太容易，我们逆向思考：如何在a、b不相遇的情况下跳到尽可能高的位置？如果找到了这个位置，它的父亲就是LCA了。

说来也简单，从可能跳的最大步数Log2[dep[a]]（这样至多跳到0号点，不会越界）开始，不断减半步数（不用多次循环）：

for (int k = Log2[dep[a]]; k >= 0; k--)
    if (fa[a][k] != fa[b][k])
        a = fa[a][k], b = fa[b][k];

以刚刚那棵树为例，先尝试Log2[4]=2，A、B点的 $2^2$ 级祖先都是0（图中未画出），所以不跳。然后尝试1，A、B的 $2^1$ 祖先都是2，也不跳。最后尝试0，A、B的1级祖先分别是4和5，跳。结束。

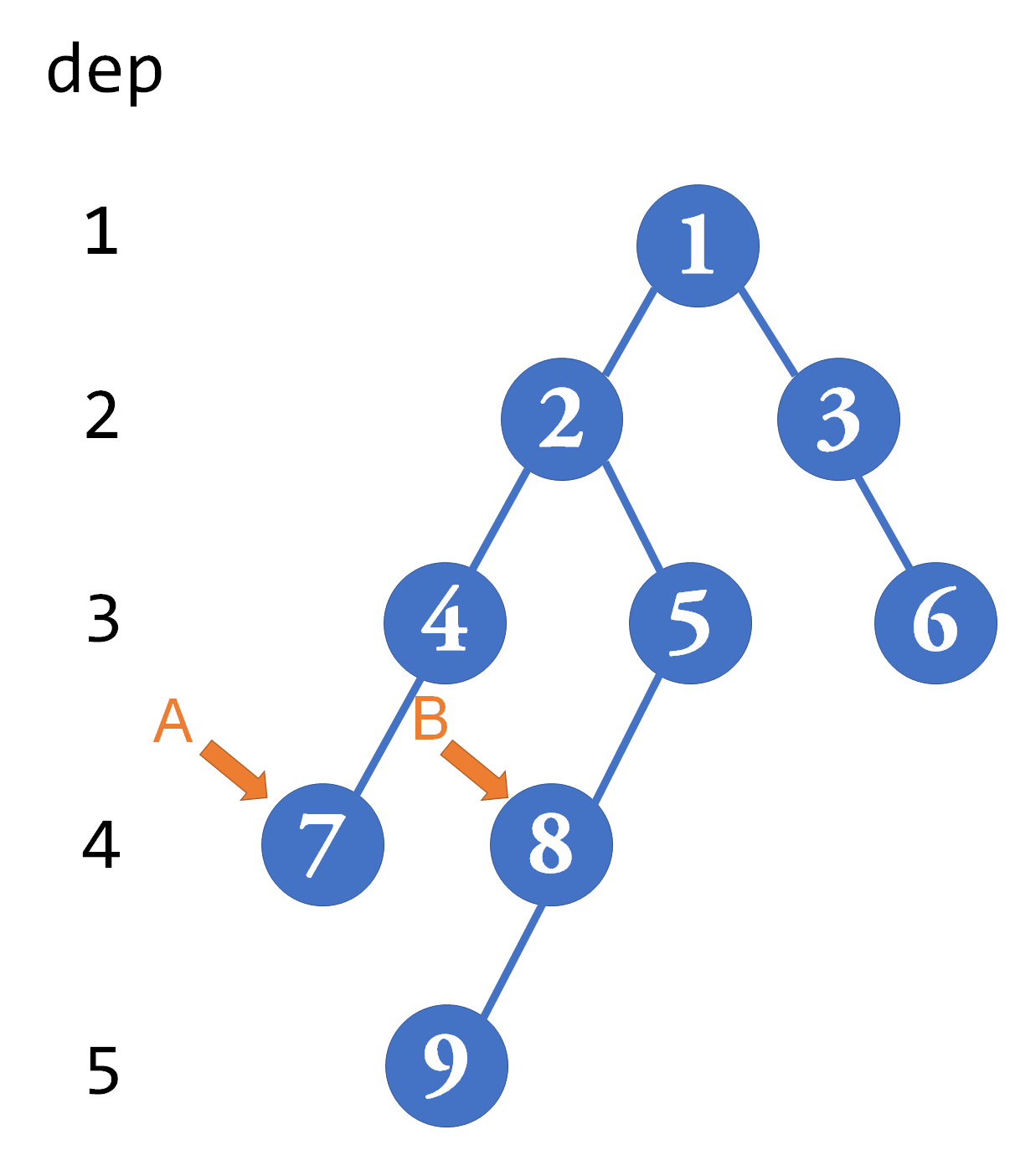
这样下来，再往上一格所得到的2号点就是所求的最近公共祖先。

主要代码如下：

int Log2[MAXN], fa[MAXN][20], dep[MAXN]; // fa的第二维大小不应小于log2(MAXN)
bool vis[MAXN];
void dfs(int cur, int fath = 0)
{
    if (vis[cur])
        return;
    vis[cur] = true;
    dep[cur] = dep[fath] + 1;
    fa[cur][0] = fath;
    for (int i = 1; i <= Log2[dep[cur]]; ++i)
        fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
    for (int eg = head[cur]; eg != 0; eg = edges[eg].next)
        dfs(edges[eg].to, cur);
}
int lca(int a, int b)
{
    if (dep[a] > dep[b])
        swap(a, b);
    while (dep[a] != dep[b])
        b = fa[b][Log2[dep[b] - dep[a]]];
    if (a == b)
        return a;
    for (int k = Log2[dep[a]]; k >= 0; k--)
        if (fa[a][k] != fa[b][k])
            a = fa[a][k], b = fa[b][k];
    return fa[a][0];
}
int main()
{
    // ...
    for (int i = 2; i <= n; ++i)
        Log2[i] = Log2[i / 2] + 1;
    // ...
    dfs(s); // 无根树可以随意选一点为根
    // ...
    return 0;
}

至于树上两点 $u,v$ 的距离，有公式 $dis_{u,v}=dep_u+dep_v-2dep_{\mathrm{LCA}(u,v)}$ （很好推）。 $O(n\log n)$ 预处理， $O(\log n)$ 查询，空间复杂度为 $O(n\log n)$ 。