圖解AI數學基礎 | 線性代數與矩陣論
- 2022 年 2 月 24 日
- 筆記
作者：韓信子@ShowMeAI 教程地址：//www.showmeai.tech/tutorials/83 本文地址：/ …
Continue ReadingSVD專題1 運算元的奇異值分解——矩陣形式的推導
- 2021 年 11 月 14 日
- 筆記
目錄 SVD專題1 運算元的奇異值分解——矩陣形式的推導 前言 Preface 幾點說明 預備知識 Prerequisit …
Continue Reading線性代數問題集錦
- 2021 年 11 月 7 日
- 筆記
如何理解線性代數中當一個矩陣的值不等於零，其就代表組成矩陣的向量線性無關？ 矩陣的秩按定義就是構成矩陣的線性無關向量的數 …
Continue Reading線性代數1 行列式
- 2021 年 6 月 6 日
- 筆記
二階行列式 所謂二階行列式，是由四個數，如 \(a_{11}\)，\(a_{12}\)，\(a_{21}\)，\(a_{ …
Continue ReadingCauchy-Binet 公式的應用
- 2021 年 5 月 8 日
- 筆記
Binet-Cauchy 公式 我們知道，方陣的行列式不是方陣的線性函數，即對 \(\forall \lambda\in …
Continue Reading特徵向量和特徵值
- 2021 年 2 月 8 日
- 筆記
特徵向量和特徵值 定義1：\(A\)為\(n\times n\)的矩陣，\(x\)為非零向量，若存在\(\lambda\ …
Continue Reading兩個多維高斯分布之間的KL散度推導
- 2020 年 10 月 12 日
- 筆記
在深度學習中，我們通常對模型進行抽樣並計算與真實樣本之間的損失，來估計模型分布與真實分布之間的差異。並且損失可以定義 …
Continue Reading機器學習 | SVD矩陣分解演算法，對矩陣做拆分，然後呢？
- 2020 年 7 月 17 日
- 筆記
本文始發於個人公眾號：TechFlow，原創不易，求個關注 今天是機器學習專題第28篇文章，我們來聊聊SVD演算法。 SV …
Continue Reading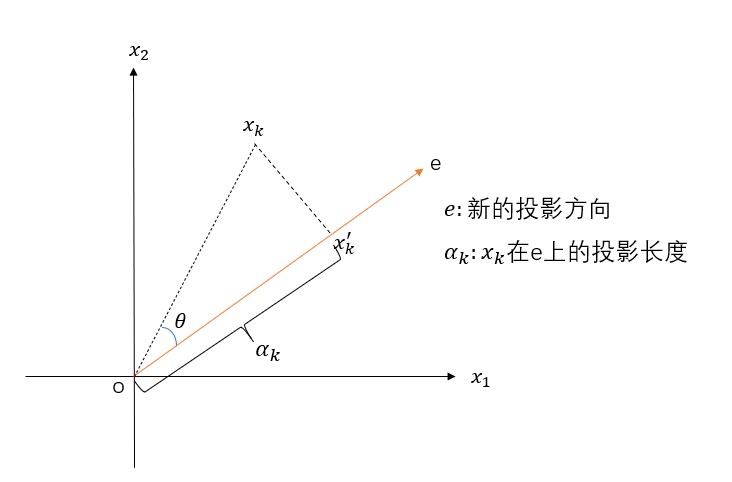
淺談 PCA與SVD
- 2020 年 4 月 14 日
- 筆記
前言 在用數據對模型進行訓練時，通常會遇到維度過高，也就是數據的特徵太多的問題，有時特徵之間還存在一定的相關性，這時如果 …
Continue Reading