數據挖掘入門系列教程（十）之k-means演算法

2020 年 4 月 23 日
筆記
數據挖掘

簡介

這一次我們來講一下比較輕鬆簡單的數據挖掘的演算法——K-Means演算法。K-Means演算法是一種無監督的聚類演算法。什麼叫無監督呢？就是對於訓練集的數據，在訓練的過程中，並沒有告訴訓練演算法某一個數據屬於哪一個類別。對於K-Means演算法來說，他就是通過某一些騷操作，將一堆「相似」的數據聚集在一起然後當作同一個類別。例如下圖：最後將數據聚集成了3個類別。

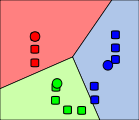
K-Means演算法中的\(K\)就是代表類別的個數，它可以根據用戶的需求進行確定，也可以使用某一些方法進行確定（比如說elbow method）。

演算法

演算法簡介

對於給定的樣本集\(D=\left\{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \ldots, \boldsymbol{x}_{m}\right\}\)，k-means演算法針對聚類所得到的簇為\(\mathcal{C}=\left\{C_{1}, C_{2}, \ldots, C_{k}\right\}\)，則劃分的最小化平方誤差為：

\[\begin{equation}
E=\sum_{i=1}^{k} \sum_{\boldsymbol{x} \in C_{i}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{i}\right\|_{2}^{2} \\
其中\boldsymbol{\mu}_{i}=\frac{1}{\left|C_{i}\right|} \sum_{\boldsymbol{x} \in C_{i}}x
\end{equation}
\]

\(E\)越小則表示數據集樣本中相似度越高。我們想得到最小的\(E\)，但是直接求解並不容易，因此我們採用啟發式演算法進行求解。

演算法流程

演算法的流程很簡單，如下所示：

選取初始化質心

首先假如我們有如下的數據集，我們隨機選取\(k\)個點（稱之為質心，這裡\(k =3\)），也就是下圖中紅綠藍三個點。

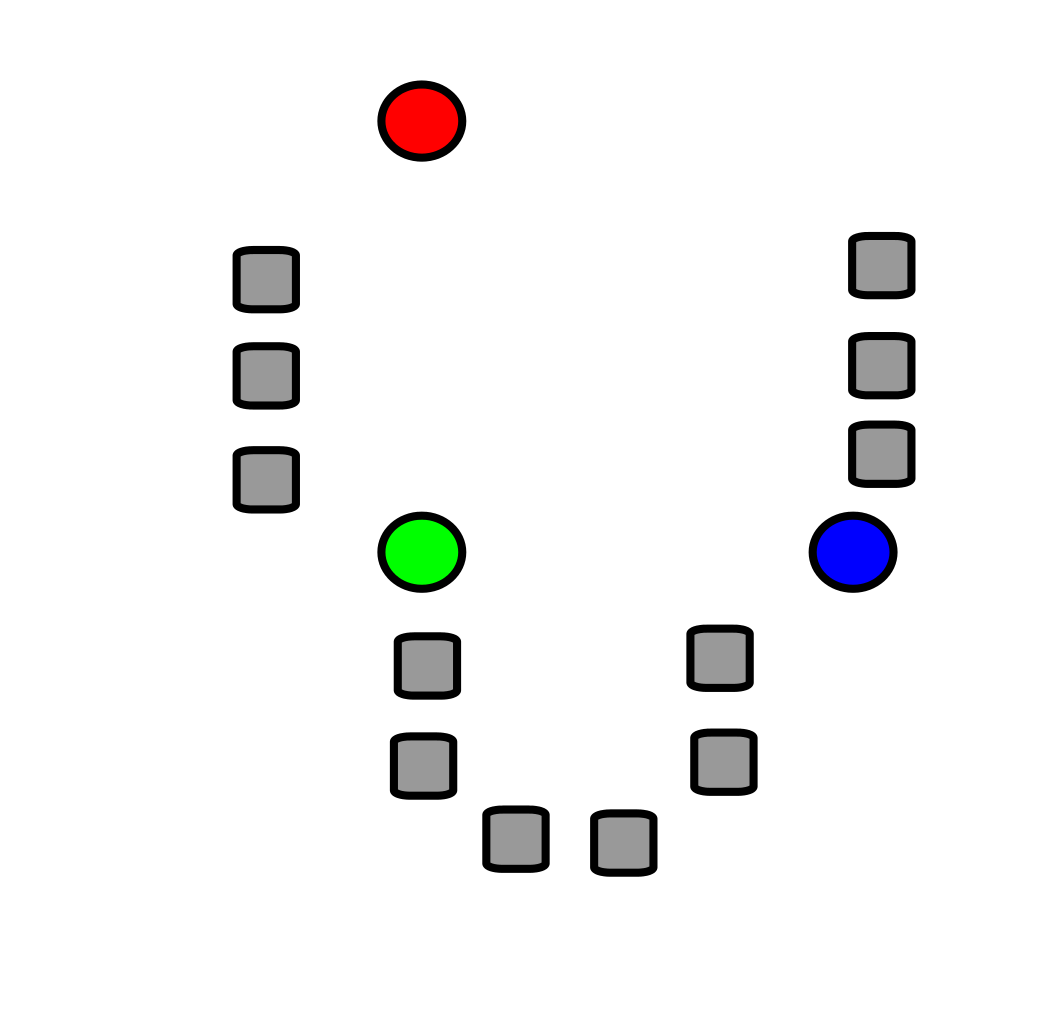
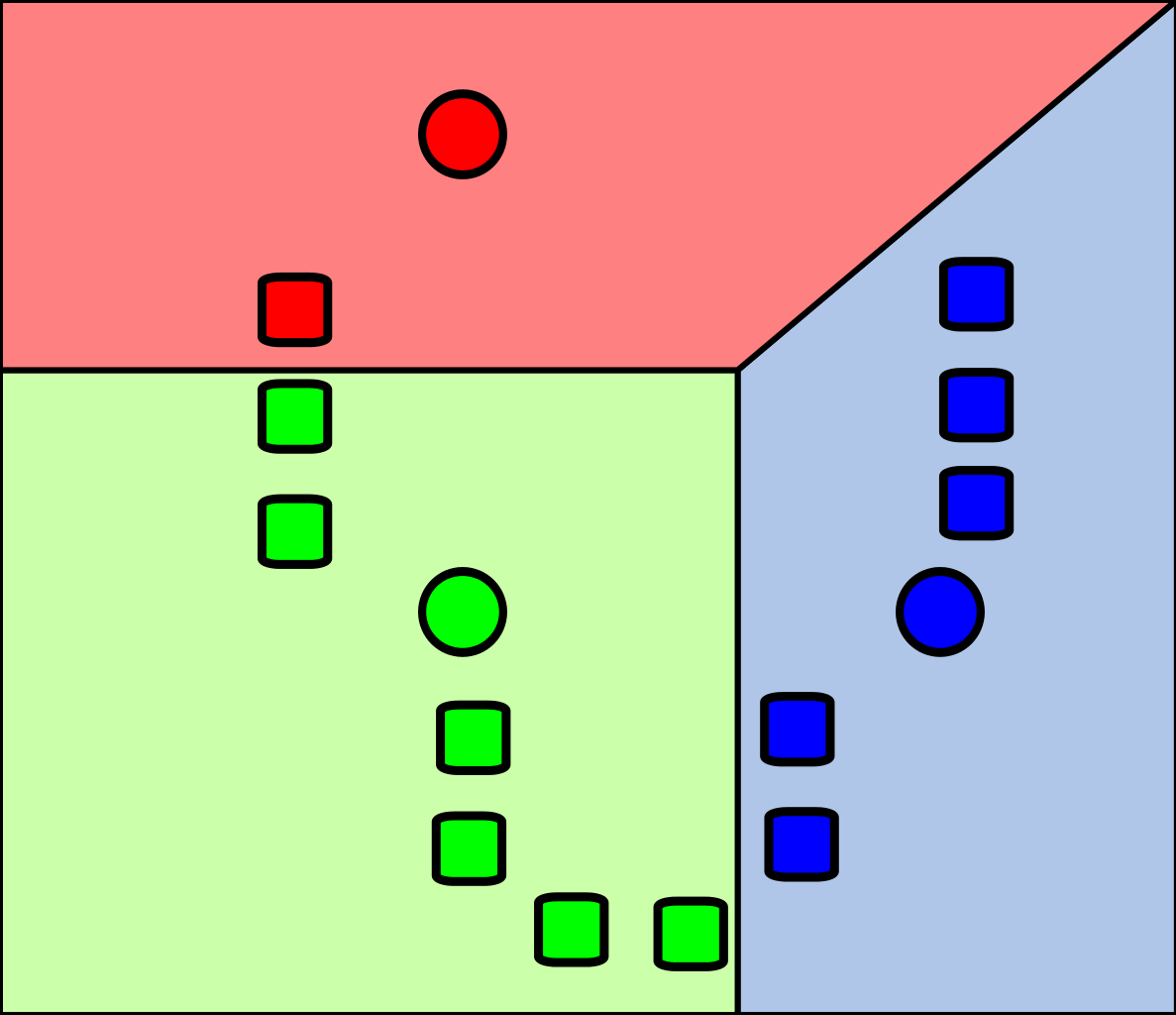
計算數據集樣本中其它的點到質心的距離，然後選取最近質心的類別作為自己的類別。

我們可以將其理解為「近朱者赤近墨者黑」，對於樣本點來說，哪個質心離我近，我就認誰做「爸爸」。同時對於「距離」，有很多種計算方式，比如說「歐氏距離」，「曼哈頓距離」等等。
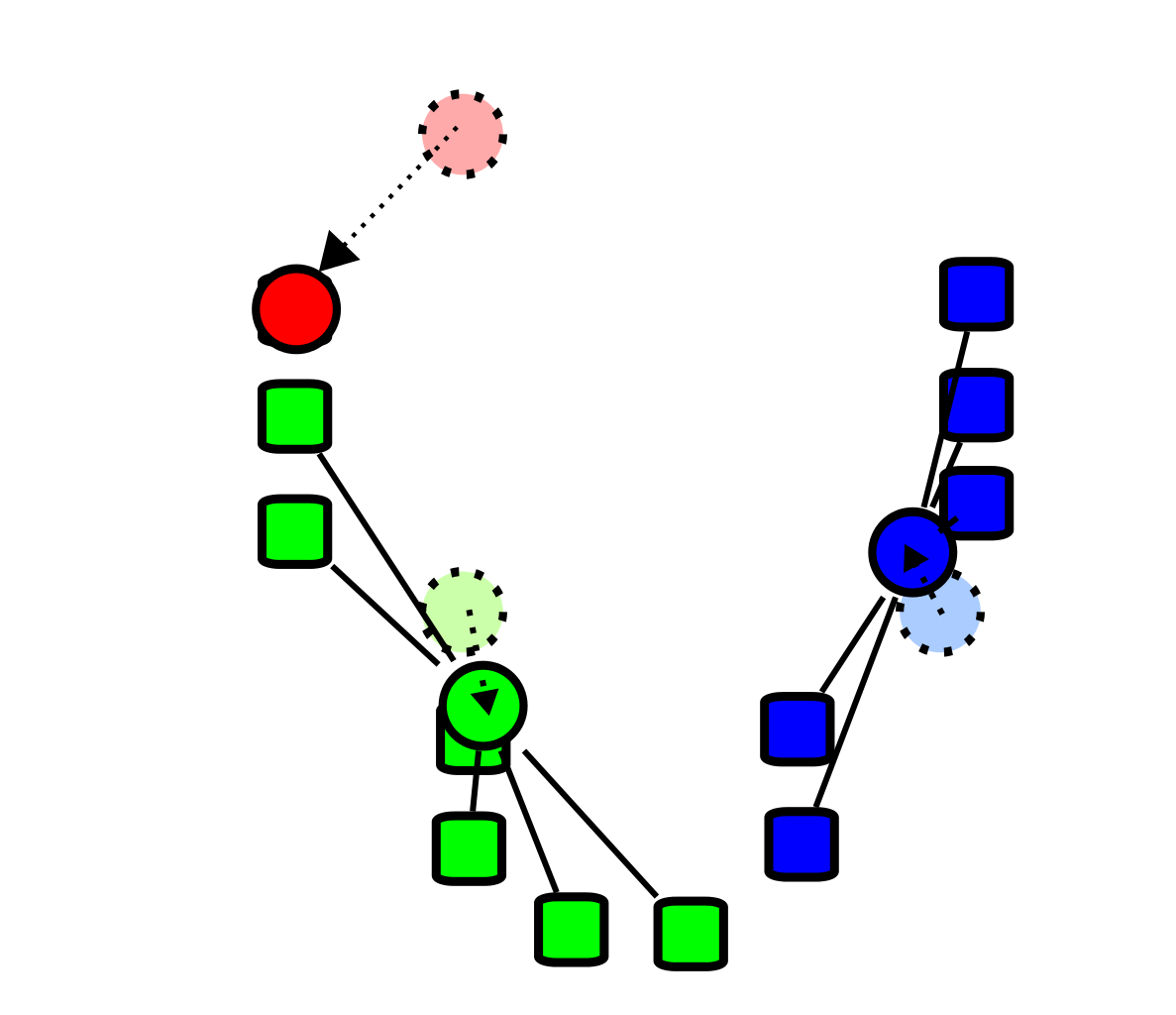
重新計算質心

通過上面的步驟我們就得到了3個簇，然後我們從這三個簇中重新選舉質心，也就是我們選舉出一個新的「爸爸」，這個”爸爸”可以為樣本點（比如說紅點），也可以不是樣本中的點（比如說藍點和綠色點）。選舉方式很簡單，就是計算每一個簇中樣本點的平均值。
重新進行劃分

按照第二步的計算方法重新對樣本進行劃分。
重複第3，4步驟，直到達到某一個閾值

這個閾值可以是迭代的輪數，也可以是當質心不發生改變的時候或者質心變化的幅度小於某一個值得時候停止迭代。

這裡引用《西瓜書》中得演算法步驟：

演算法gif圖如下所示：

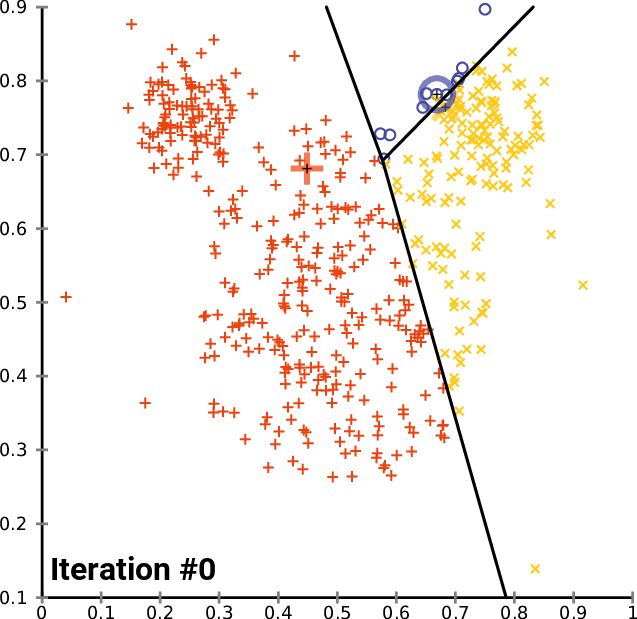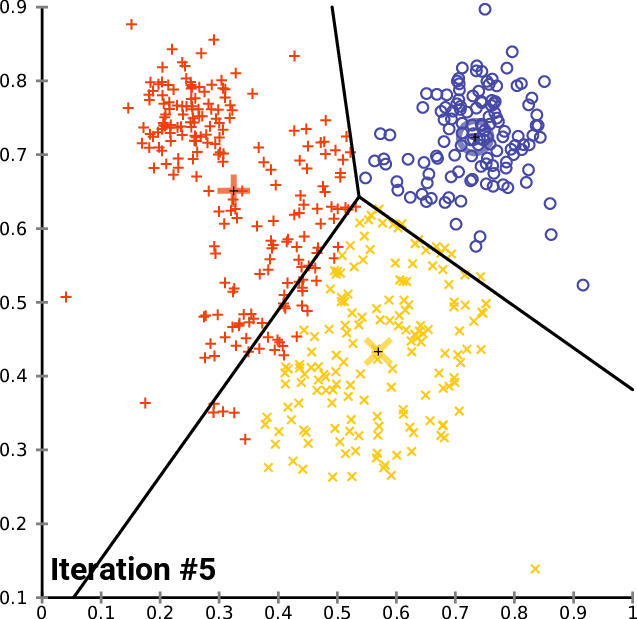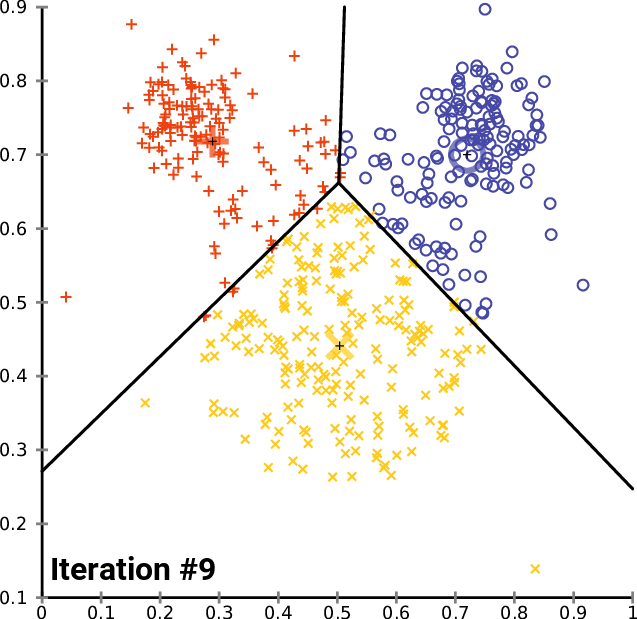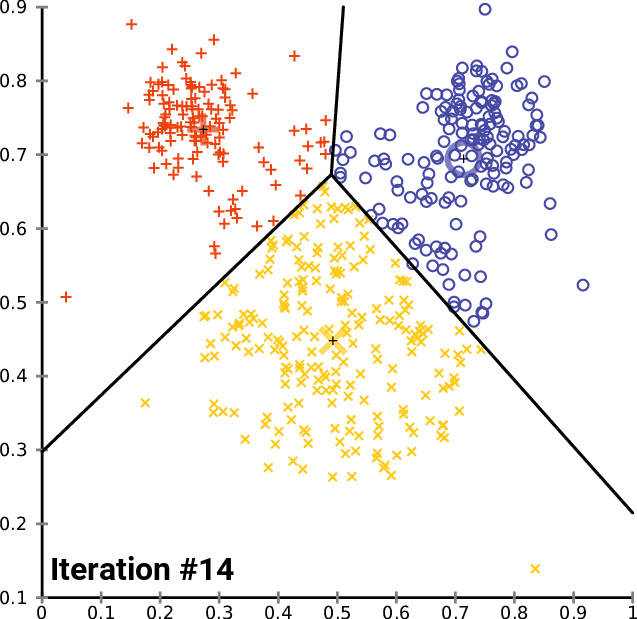
演算法的優化

K-Means演算法的步驟就如上所示，但是實際上裡面還有一些細節可以進行優化。

K-Means++演算法

在上面我們討論了k-means演算法的流程，當時我們可以仔細想一想，如果在第一步初始化質心的步驟中，如果質心選擇的位置不是特別的好，比如說三個點挨在一起，那這樣，我們必定會需要使用大量的迭代步驟。同時它還可能影響著最後簇的結果。為了解決這個誤差，我們可以選擇一組隨機的初始化質心，然後選取最小的\(E\)值（也就是是最小化平方誤差最小）。

當然，我們也有其他的方法。

K-Means++演算法與上面傳統的K-means演算法不同的點就在於它使用了一定的方法使得演算法中的第一步（初始化質心）變得比較合理，而不是隨機的選擇質心。演算法的步驟如下：

從輸入樣本中隨機選擇一個樣本作為質心\(\mu_1\)
對於數據集中的每一個樣本\(x_i\)，計算它他與已選擇的質心\(\mu_r\)的距離，設樣本\(x_i\)到質心的距離為\(D(x_i)\) 【這個距離肯定是離質心的最短距離】，因此\(D(x_i) = arg\;min||x_i- \mu_r||_2^2\;\;r=1,2,…k_{selected}\)。
選擇一個新的數據樣本作為新的質心，選擇的原則為：\(D(x_i)\)越大，被選擇的概率也就越大。
重複2，3步驟直到選取出\(k\)個質心。
運行傳統k-means演算法中的第2，3，4，5步。

K-Means++實際上就是改變了初始化質心的步驟，其他的步驟並沒有發生改變。

K-Means演算法中距離計算的優化

假設我們有\(n+k\)個樣本（其中有\(k\)個質心），毋庸置疑，我們需要計算\(n\)個樣本到\(k\)個質心的距離。這一步我們可以稍微的簡化一下。運用三角形兩邊之和大於第三邊我們可以知道：

\[a+b \gt c\\
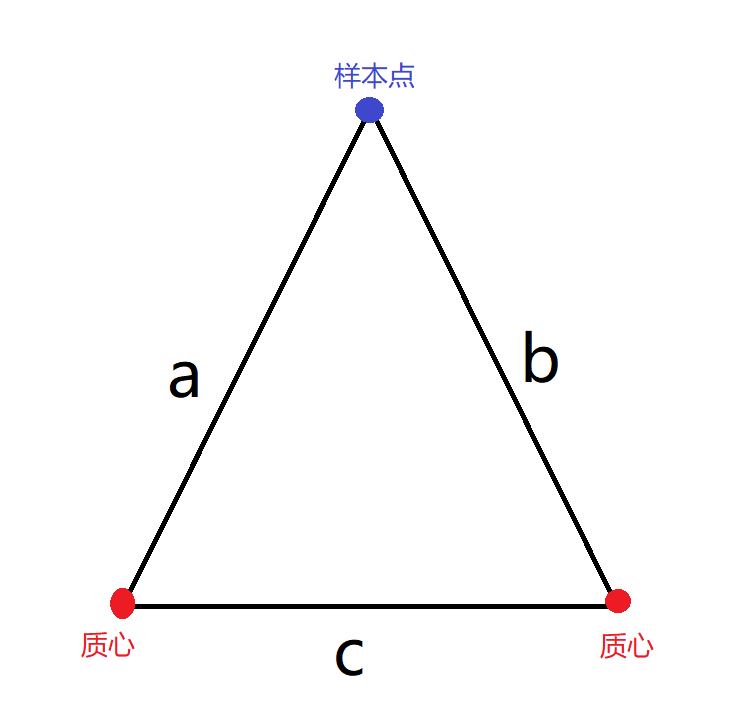
a – b \lt c \\
因此則有：\\
b \geq max\{0,a – c\} \\
若2a \le c,則有\\
a \le b \\
\]

利用上面的這兩條規矩，我們就可以在一定程度上簡化計算。

K值的確定

前面我們說過\(K\)值代表著簇數，我們可以按照需求來給定，也可以通過計算的方法給一個比較合理的\(K\)值。下面就來介紹一下「elbow method」來確定合理的\(K\)值，關於更多的方法，可以參考一下維基百科。

Elbow Method

Elbow Method原理很簡單，我們給定\(K\)的一個範圍，比如說是從0~10，然後我們分別計算每一個K值對應的SSE，也就是前面的最小化平方誤差\(E\)，然後我們再將每一個\(K\)值對應的SSE畫出來。可以很簡單的知道，隨著\(K\)值的增大，SSE會趨向於0（假如每一個樣本點都是質心，那麼對應的距離\(E\)就是0了）。我們往往希望得到一個較小的SSE，同時保證\(K\)值也比較小。

我們可以將\(K\)值對應的SSE圖看成一個手臂，則我們選取的\(K\)的地方就是「肘（elbow）」這個地方，這裡是拐彎最大的地方。

基於sklearn的K-Means演算法使用

產生數據集

首先的首先，我們需要一個數據集，這裡我們使用sklearn中的make_blobs來生成各向同性高斯團簇。然後再將數據進行畫圖：

import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
# 數據集的個數
data_num = 1000
# k值，同時也是生成數據集的中心點
k_num  = 4

# 生成聚類數據，默認n_features為二，代表二維數據，centers表示生成數據集的中心點個數，random_state隨機種子
data,y=ds.make_blobs(n_samples=data_num,centers=k_num,random_state=0)

data為二維坐標，y為數據標籤，從0到3。畫圖程式碼如下：

# 不同的數據簇用不同的顏色表示
data_colors = matplotlib.colors.ListedColormap(['red','blue','yellow','Cyan'])
# data為二維數據
plt.scatter(data[:,0],data[:,1],c=y,cmap=data_colors)
plt.title("orginal data")
plt.grid()
plt.show()

畫圖如下所示

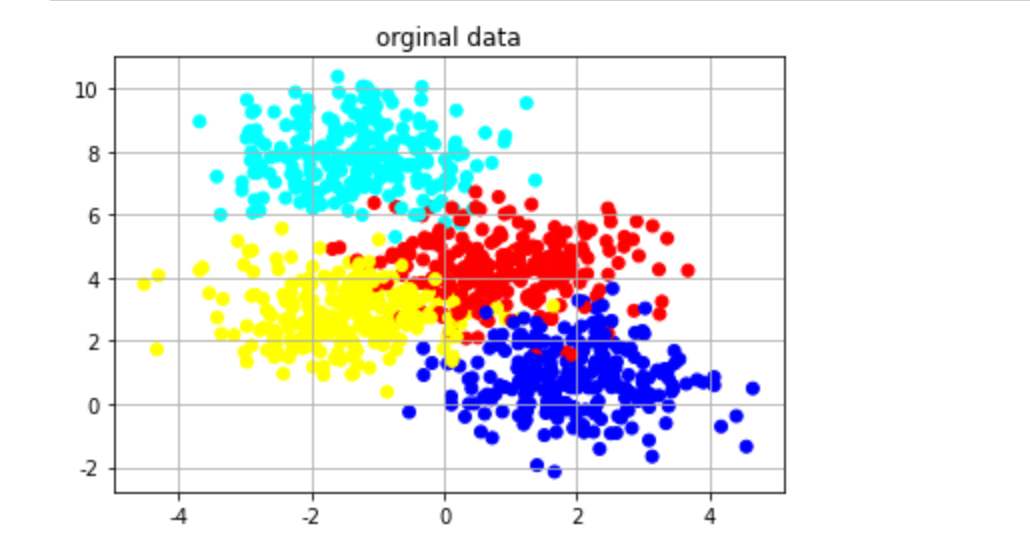
使用k-means

我們可以使用cluster包下的KMeans來使用k-means演算法，具體參數可以看官方文檔。

'''
sklearn.cluster.KMeans(
	n_clusters=8, 
	init='k-means++', 
	n_init=10, 
	max_iter=300, 
	tol=0.0001, 
	precompute_distances='auto', 
	verbose=0, 
	random_state=None, 
	copy_x=True, 
	n_jobs=1, 
	algorithm='auto' )
參數說明：
(1)n_clusters:簇的個數，也就是k值
(2)init: 初始簇中心的方式，可以為k-means++,也可以為random
(3)n_init: k-means演算法在不同隨機質心情況下迭代的次數，最後的結果會輸出最好的結果
(4)max_iter: k-means演算法最大的迭代次數
(5)tol: 關於收斂的相對公差
(8)random_state: 初始化質心的隨機種子
(10)n_jobs: 並行工作，-1代表使用所有的處理器
'''
from sklearn.cluster import KMeans
model=KMeans(n_clusters=k_num,init='k-means++')
# 訓練
model.fit(data)
# 分類預測
y_pre= model.predict(data)

然後我們可以將預測分類結果畫出來：

plt.scatter(data[:,0],data[:,1],c=y_pre,cmap=data_colors)
plt.title("k-means' result")
plt.grid()
plt.show()

總結

當然，k-means對於某一些分類任務還是比較困難，如下：

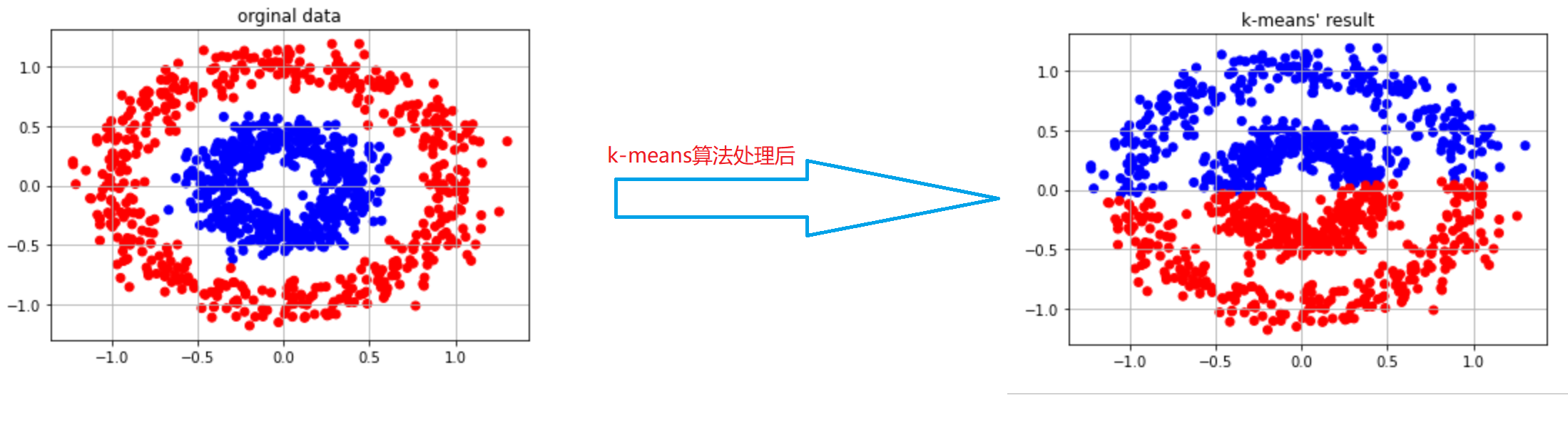
很明顯，我們應該將數據分成內圈和外圈，但是呢，使用k-means演算法後，將數據集分成了上下兩個部分，這樣肯定是不對的。

總的來說，k-means演算法還是比較簡單的，沒有什麼複雜的地方，也易於實現。

項目地址：Github

參考

k-means clustering
《西瓜書》
K-Means聚類演算法原理
Determining the number of clusters in a data set
elbow method

Tags: 數據挖掘