01背包_順序枚舉和逆序枚舉的問題_一維數組
逆序枚舉和順序枚舉差異主要在一維數組實現的時候出現
方程: dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
測試樣例:
3 5
3 5 2 6 4 10
逆序結果: 11
順序結果: 12
12這個錯誤的數據是怎麼來的?
利用check,列印每次枚舉後的結果, 程式碼如下


1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 using namespace std; 5 const int M=1e5+10; 6 int w[M],v[M]; 7 int n,m; 8 int dp[M]; 9 10 int T; 11 void check(int i,int j) { 12 13 cout<<"容量為"<<j<<"的背包中,"<<"放入第"<<i<<"個物品\n"; 14 printf("容量: "); 15 for(int k=1; k<=m; k++) { 16 cout<<k<<" "; 17 } 18 printf("\n價值: "); 19 for(int k=1; k<=m; k++) { 20 cout<<dp[k]<<" "; 21 } 22 puts("\n\n"); 23 } 24 /* 25 3 5 26 3 5 2 6 4 10 27 28 */ 29 void f1() { 30 memset(dp,0,sizeof(dp)); 31 //dp[j]=max(dp[j],dp[j-w[i]]+v[i]);i(1,n),j>=w[i], 32 //容量初始值j=m 33 //決策時i為常數, 所以 i 在最外層 34 for(int i=1; i<=n; i++) { 35 /* 36 for(int j=m; j>=w[i]; j--) { // 37 dp[j]=max(dp[j],dp[j-w[i]]+v[i]); 38 }*/ 39 for(int j=1; j<=m; j++) { 40 if(j>=w[i])dp[j]=max(dp[j],dp[j-w[i]]+v[i]); 41 check(i,j); 42 } 43 } 44 cout<<dp[m]<<endl; 45 } 46 void f2() { 47 memset(dp,0,sizeof(dp)); 48 //dp[j]=max(dp[j],dp[j-w[i]]+v[i]);i(1,n),j>=w[i], 49 //容量初始值j=m 50 //決策時i為常數, 所以 i 在最外層 51 for(int i=1; i<=n; i++) { 52 53 for(int j=m; j>=w[i]; j--) { // 54 dp[j]=max(dp[j],dp[j-w[i]]+v[i]); 55 check(i,j); 56 } 57 58 } 59 cout<<dp[m]<<endl; 60 } 61 /* 62 5 1000 63 144 990 64 487 436 65 210 673 66 567 58 67 1056 897 68 69 2099 70 */ 71 int main() { 72 73 cin>>n>>m; 74 for(int i=1; i<=n; i++)cin>>w[i]>>v[i]; 75 f1(); 76 system("pause"); 77 f2(); 78 79 return 0; 80 }
View Code
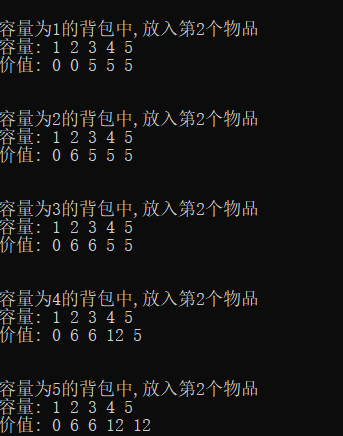
對於放入第2個物品,容量為3的枚舉,dp[3]= 6, 6= dp[3-2]+6
對於放入第2個物品,容量為4的枚舉,dp[4]= 12, 12= dp[4-2]+6
在第4次枚舉的時候發現問題,
原因在於dp[4]=dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
dp[4]=dp[2]+6 = 6+6
然鵝,dp[2]已經更新過,通過裝入物品2,
此時dp[2]的值是容量為2的時候的最大值,
在這個過程里, 第2個背包被使用了兩次,
重複枚舉就是利用先更新容量小的背包實現的
而dp[5]則是直接繼承了dp[4]
每次都利用之前的最大值,並且每個背包都放進去試一試, 可以繼承已經更新過的–前驅背包的–“最大價值”, 也就可以重複無限次,
這樣枚舉出來的結果是完全背包的最大價值
============//=============
而逆序枚舉呢?
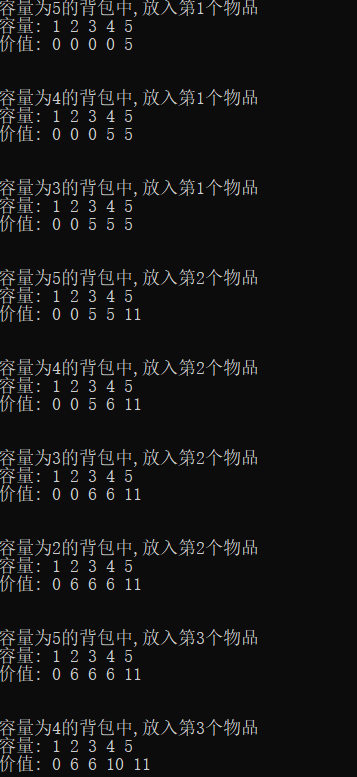
和順序枚舉不一樣的地方從放入第2個物品開始,
逆序 dp[5]=dp[5-2]+6=dp[3]+6, 一樣用的是之前更新過的最大值,
但是區別在於, 之前更新過的dp[3], 並沒有被第2個物品放入過, 也就是說沒有被枚舉更新過, 也就是說不存在重複更新,
同理, dp[4] =dp[4-2]+6=dp[2]+6;
此時dp[2]=0, 還沒有被更新過,還沒有嘗試放入第2個物品過,
不存在: 容量小的背包在容量大的背包被更新之前就更新過
結論: 順序枚舉的結果是可取無限次物品的結果, 逆序結果得到的是每種物品只取一次的結果


