線段樹(區間樹)
- 2020 年 4 月 12 日
- 筆記
為什麼要使用線段樹?
最經典的線段樹問題:區間染色
有一面牆 ,長度為n,每次選擇一段兒牆進行染色,m次操作後,我們可以看見多少種顏色?

例如上圖,我們第一次將[1,8]的位置染成藍色,然後再將[5,9]的位置染成黃色,然後將[6,15]的位置染成紅色,最後把[12,15]的顏色染成綠色,我們通過這幾次操作可以發現,圖中被重複染色的位置是會被覆蓋的,比如[12,15]這個位置顯示被染成紅色,然後又被染成了綠色,但最後呈現的是綠色。我們也可以把「m次操作後,我們可以看見多少種顏色」這個問題,轉化為「m次操作後,我們可以在[i, j]區間內看見多少種顏色」問題。對於這個問題我們可以使用數組來解決,但我們會發現,在使用數組實現的時候,不管是染色操作(更新區間),還是查詢操作(查詢區間),都需要對數組進行遍歷,這樣使用數組實現區間染色問題的時間複雜度就是O(n)。但這個時間複雜度的程式執行起來,數據量如果大了,執行效率是很低的。所以有了線段樹這樣的數據結構。
另一類經典問題:區間查詢

查詢一個區間[i, j]的最大值,最小值,或者區間數字和
實質上是一個基於區間的統計查詢,例如在一個學習網站:用戶想要知道2019年註冊用戶種消費最高的用戶?消費最少的用戶?學習時長最長的用戶?
當我們使用線段樹來處理這類問題時,時間複雜度為O(logn),其執行效率就要比數組實現快很多。
什麼是線段樹?
一棵二叉樹的每個節點是存儲的一個區間或者說是一個線段相應的資訊,這裡說的相應的資訊不是指把這個區間內的元素都存進去,我們以求和為例,每一個節點相應存儲的是這個節點所對應區間的數字的和。
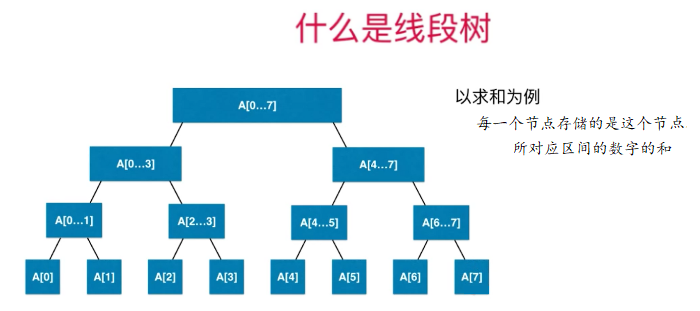
線段樹一定是滿二叉樹嗎?不一定,這裡是因為8恰好是2的三次方,剛好可以構成一顆滿二叉樹。
根節點代表整個線段,左孩子代表根節點線段的前半段,右孩子就是根節點線段的後半段。直到到了葉子節點,葉子節點只表示一個元素。如果現在數組中有十個元素,相應的線段樹就不是二叉樹了,如下:

注意:線段樹不是完全二叉樹,但線段樹是平衡二叉樹,當然堆也是平衡二叉樹。
關於平衡二叉樹和完全二叉樹的概念,由於堆是完全二叉樹,所以我在堆和優先隊列中就詳細介紹了,有興趣的小夥伴可以看一下。
什麼是完全二叉樹呢?完全二叉樹就是把元素按照樹的形狀一層一層的放,直到放完為止,即把元素順序排成樹的形狀。堆也是一棵平衡二叉樹,因為完全二叉樹一定是平衡二叉樹,什麼是平衡二叉樹?即對於整棵樹來說,最大深度和最小深度的差值不能大於1,因此平衡二叉樹一定不會退化成鏈表。滿二叉樹是特殊的完全二叉樹。
線段樹雖然是平衡二叉樹,不是完全二叉樹,但是線段樹任然可以使用數組來表示,如果區間有n個元素,用數組表示需要有多少個節點呢?對於滿二叉樹來說,0層有一個節點,1層有兩個節點,2層有四個節點,3層有8個節點,則在h層一共有2h-1個節點(大約是2h個),最後一層(h-1層),有2(h-1)個節點,即滿二叉樹最後一層的節點數大致等於前面所有層節點之和。

為什麼最壞情況是如果n=2k+1,需要4n的空間呢?因為如果n=2k,就是剛好可以構成一課滿二叉樹,這時只需要2n的區間就好了,這是最好的情況,數組中每個空間都被使用,最壞的情況就是在滿二叉樹的情況下多出一個節點,由於我們數組是存儲的相當於滿二叉樹的節點個數,所以需要數組2n+2n=4n的空間,但實際上這2n的空間中只有一個節點是有效數據,其他2n-1的空間都是浪費掉的。
所以為了考慮到最壞的情況,如果區間有n個元素,數組表示需要4n的空間,由於我們的線段樹不考慮添加元素,即區間固定,使用4n的靜態空間就可以了。
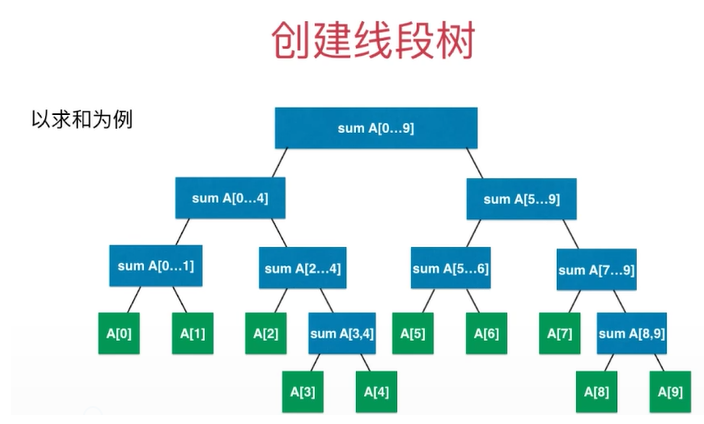
創建一棵線段樹
程式碼實現如下:
public class SegmentTree<E> { private E[] data; private E[] tree; //構造函數 -- 通過用戶傳遞的數組構建一顆吸納段數 public SegmentTree(E[] arr){ this.data = (E[])new Object[arr.length]; for (int i=0; i<arr.length; i++){ data[i] = arr[i]; } //創建一個空間為4n的靜態數組 tree = (E[])new Object[arr.length*4]; } //獲取線段樹中實際元素的個數 public int getSize(){ return data.length; } //查找元素 public E get(int index){ if (index < 0 || index >= data.length ){ throw new IllegalArgumentException("Index is Illegal"); } return data[index]; } } 根據我們在堆和優先隊列所講到過的,由於完全二叉樹可以使用數組表示,因此我們可以找出數組中的所以和完全二叉樹中節點的關係,我們在堆和優先隊列中已經推到過關係了,雖然線段樹不是完全二叉樹,但由於線段樹是平衡二叉樹,所以我們在處理時,是將線段樹作為滿二叉樹在進行處理,滿二叉樹又是特殊的完全二叉樹,所以線段樹也可以使用數組來表示,線段樹使用數組表示時,其索引與節點的關係如下:
//左孩子節點的索引 public int leftChild(int index){ return index*2 + 1; } //有孩子節點的索引 public int rightChild(int index){ return index*2 + 2; } 由於我們線段樹中節點存儲的不是元素,而是存儲的這個區間以某種方法合併後的值,比如是存儲的這個區間中元素的最大值,最小值,或者是這個區間中的元素之和等。所以我們需要在創建線段樹的構造函數中,添加一個合併方法,讓用戶在使用時去確定是以何種方式合併這個區間中的元素的,如下:
先創建一個合併方法的介面:
public interface Merger<E> { E merge(E a, E b); } 下面讓我們來看看如何構建一顆線段樹吧:
private Merger<E> merger; public SegmentTree(E[] arr, Merger<E> merger){ //合併的方法 this.merger = merger; this.data = (E[])new Object[arr.length]; for (int i=0; i<arr.length; i++){ data[i] = arr[i]; } //創建一個空間為4n的靜態數組 tree = (E[])new Object[arr.length*4]; //遞歸構建一顆線段樹 buildSegmentTree(0,0,arr.length-1); } // 在treeIndex的位置創建表示區間[l...r]的線段樹 private void buildSegmentTree(int treeIndex, int l, int r) { //遞歸終止條件,即到了葉子節點 if (l == r){ tree[treeIndex] = data[l]; return; } //獲取當前節點的左孩子索引 int leftTreeIndex = leftChild(treeIndex); //獲取當前節點的右孩子索引 int rightTreeIndex = rightChild(treeIndex); //int mid = (l + r) / 2 該方式可能會導致整型溢出 int mid = l + (r-l)/2; //遞歸構建左子樹 buildSegmentTree(leftTreeIndex,l,mid); //遞歸構建右子樹 buildSegmentTree(rightTreeIndex,mid+1,r); //合併左子樹和右子樹所代表的區間 tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]); } 現在就讓我們來測試一下我們自己寫的線段樹是否正確吧,為了更直觀的看輸出結果,我們重寫一下SegmentTree的toString()方法:
@Override public String toString() { StringBuilder res = new StringBuilder(); res.append("["); for (int i=0; i<tree.length; i++){ if (tree[i] == null){ res.append("null"); }else { res.append(tree[i]); } if (i != tree.length-1){ res.append(","); } } res.append("]"); return res.toString(); } 這裡以求和為例進行測試:在測試中為了程式碼的簡潔性我使用的時Lambda表達式,若你不了解Lambda表達式的使用,你也可以使用匿名內部類進行測試,當然你可以去看我之前寫的Lambda表達式學習筆記進行學習
public static void main(String[] args) { Integer[] nums = {-2, 0, 3, -5, 2, -1}; SegmentTree<Integer> segTree = new SegmentTree<>(nums, (a, b) -> a + b); System.out.println(segTree); } 測試程式碼結果分析:
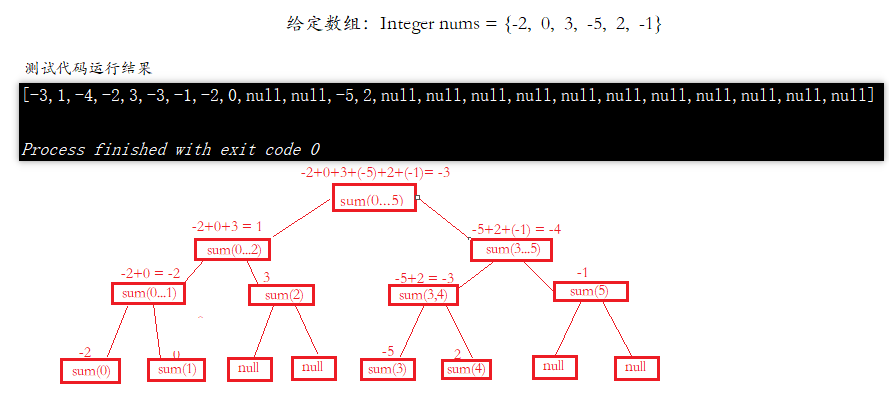
由於我們的線段樹在使用數組表示時,為其分配了用戶給定數組長度的四倍,所有會多出一些空間,這些空間的值都默認為空。
線段樹的查詢操作
線段樹的查詢操作如下:
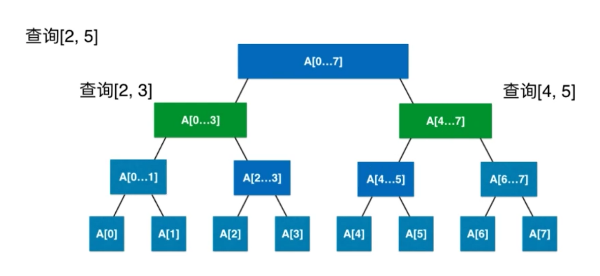
在這個過程中,我們不需要從頭到尾遍歷我們需要查詢的區間,我么只需要從我們的線段樹上,從根節點想下去找相應的子區間,最後把我們找到的這些子區間在全都組合起來就可以了。這個過程是和整棵樹的高度相關的,而和需要查詢區間的長度是沒關的,而我們整棵樹的高度是LogN級別的,所以我們查詢操作也是LogN的。
程式碼實現如下:
// 在以treeIndex為根的線段樹中[l...r]的範圍里,搜索區間[queryL...queryR]的值 private E query(int treeIndex, int l, int r, int queryL, int queryR) { if (l==queryL && r==queryR){ return tree[treeIndex]; } int mid = l + (r-l)/2 ; // treeIndex的節點分為[l...mid]和[mid+1...r]兩部分 int leftTreeIndex = leftChild(treeIndex); int rightTreeIndex = rightChild(treeIndex); if (queryL >= mid+1){ return query(rightTreeIndex,mid+1,r,queryL,queryR); }else if (queryR <= mid){ return query(leftTreeIndex,l,mid,queryL,queryR); } E leftResult = query(leftTreeIndex, l, mid, queryL, mid); E rightResult = query(rightTreeIndex,mid+1, r,mid+1,queryR); return merger.merge(leftResult,rightResult); } 線段樹的查詢操作,我們已經寫完了,現在來進行測試:這裡還是以求和為例
public static void main(String[] args) { Integer[] nums = {-2, 0, 3, -5, 2, -1}; SegmentTree<Integer> segTree = new SegmentTree<>(nums, (a, b) -> a + b); System.out.println(segTree); System.out.println(segTree.query(0, 2)); System.out.println(segTree.query(2, 5)); System.out.println(segTree.query(0, 5)); } 運行結果如下:
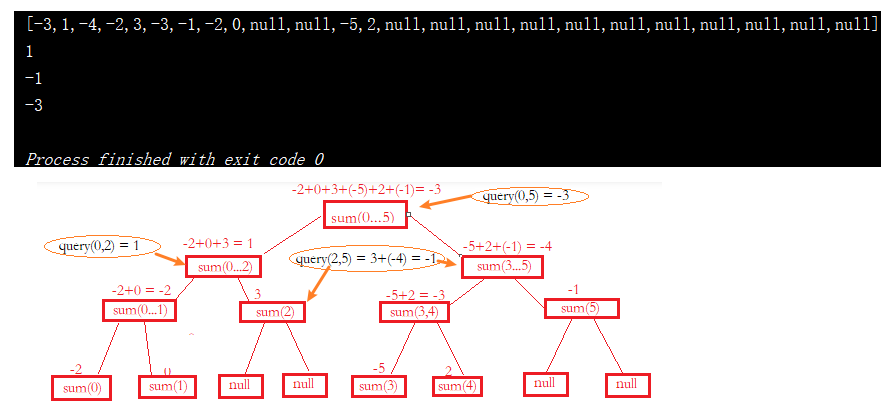
線段樹的更新操作
在講線段樹的更新操作之前,我們先來看一個leetcode上的問題:就是303號問題,區域和檢索 – 不可變,具體題目描述請上leetcode官網進行搜索題號進行查看:

可以看到題目描述的資訊和我們的測試程式碼運行結果相同,我們使用自己實現的線段樹,可以很簡單的解決這個問題:
//使用我們的自定義線段樹 private SegmentTree<Integer> segmentTree; public NumArray(int[] nums) { if (nums.length > 0){ Integer[] data = new Integer[nums.length]; for (int i=0; i<nums.length; i++){ data[i] = nums[i]; } segmentTree = new SegmentTree<>(data,(a, b) -> a+b); } } public int sumRange(int i, int j) { if (segmentTree == null){ throw new IllegalArgumentException("segmentTree is null"); } return segmentTree.query(i,j); } 由於這個問題中的數組是不可變的,所以我們不需要這麼麻煩,我們可以通過預處理的方式來進行處理,如下:
private int[] sum; public NumArray(int[] nums) { sum = new int[nums.length + 1]; sum[0] = 0; for(int i = 1 ; i < sum.length ; i ++) // sum[i]存儲前i個元素和, sum[0] = 0 // 即sum[i]存儲nums[0...i-1]的和 // sum(i, j) = sum[j + 1] - sum[i] sum[i] = sum[i - 1] + nums[i - 1]; } public int sumRange(int i, int j) { return sum[j + 1] - sum[i]; } 接下來在看一個leetcode上的題,就是307號問題,這個問題在303號問題的基礎上,多了一個更新操作:

我們如果任然使用預處理的方式解決這個問題:
private int[] sum; private int[] data; public NumArray(int[] nums) { data = new int[nums.length]; for(int i = 0 ; i < nums.length ; i ++) data[i] = nums[i]; sum = new int[nums.length + 1]; sum[0] = 0; for(int i = 1 ; i < sum.length ; i ++) sum[i] = sum[i - 1] + nums[i - 1]; } //添加一個更新操作,每一次更新,我們都需要對sum數組中的值進行重置 public void update(int index,int val){ data[index] = val; //只需要對被修改元素值之後的和進行修改 for(int i = index+1 ; i < sum.length ; i ++) sum[i] = sum[i - 1] + data[i - 1]; } 由於每次更新操作之後,我們都需要對sum數組中的值進行重置,這個過程中的時間複雜度為O(n),下面讓我們使用線段樹來解決這個問題,在此之前,我們先看一下線段樹的更新操作:
//將index位置的值,修改為e public void set(int index,E val){ if (index<0 || index >= data.length) throw new IllegalArgumentException("index is illegal"); data[index] = val; //數組中對應的值修改後,需要維護線段樹中節點的值 set(0,0,data.length-1,index,val); } //以treeIndex為根的線段樹中更新index的值為val private void set(int treeIndex, int l, int r, int index, E val) { //遞歸終止條件 if (l == r){ tree[treeIndex] = val; return; } int mid = l + (r - l) / 2; int leftTreeIndex = leftChild(treeIndex); int rightTreeIndex = rightChild(treeIndex); //被修改元素的索引大於中間點,則去右子樹遞歸修改 if (index >= mid+1){ set(rightTreeIndex, mid+1, r, index, val); }else { //被修改元素的索引小於中間點,則去左子樹遞歸修改 set(leftTreeIndex, l, mid, index, val); } //合併左子樹和右子樹修改的值 tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]); } 現在再讓我們來解決這個307號問題:
//使用我們自己實現的線段樹 private SegmentTree<Integer> segmentTree; public NumArray(int[] nums) { if (nums.length > 0){ Integer[] data = new Integer[nums.length]; for (int i=0; i<nums.length; i++){ data[i] = nums[i]; } segmentTree = new SegmentTree<>(data,(a, b) -> a+b); } } //調用我們線段樹的更新操作 public void update(int index,int val){ if (segmentTree == null){ throw new IllegalArgumentException("segmentTree is null"); } segmentTree.set(index,val); } public int sumRange(int i, int j) { if (segmentTree == null){ throw new IllegalArgumentException("segmentTree is null"); } return segmentTree.query(i,j); } 由於我們的線段樹是平衡二叉樹,所以線段樹的查詢和更新操作的時間複雜度都是O(log n)的。本文講的是一維線段樹,當然還有二維線段樹和三維線段樹,本文就不做介紹了,你們有興趣可以去網上查閱相關資料進行學習。