非參數估計——核密度估計（Parzen窗）

• 2020 年 4 月 11 日
• 筆記

　　核密度估計，或Parzen窗，是非參數估計概率密度的一種。比如機器學習中還有K近鄰法也是非參估計的一種，不過K近鄰通常是用來判別樣本類別的，就是把樣本空間每個點劃分為與其最接近的K個訓練抽樣中，佔比最高的類別。

直方圖

　　首先從直方圖切入。對於隨機變數$X$的一組抽樣，即使$X$的值是連續的，我們也可以劃分出若干寬度相同的區間，統計這組樣本在各個區間的頻率，並畫出直方圖。下圖是均值為0，方差為2.5的正態分布。從分布中分別抽樣了100000和10000個樣本：

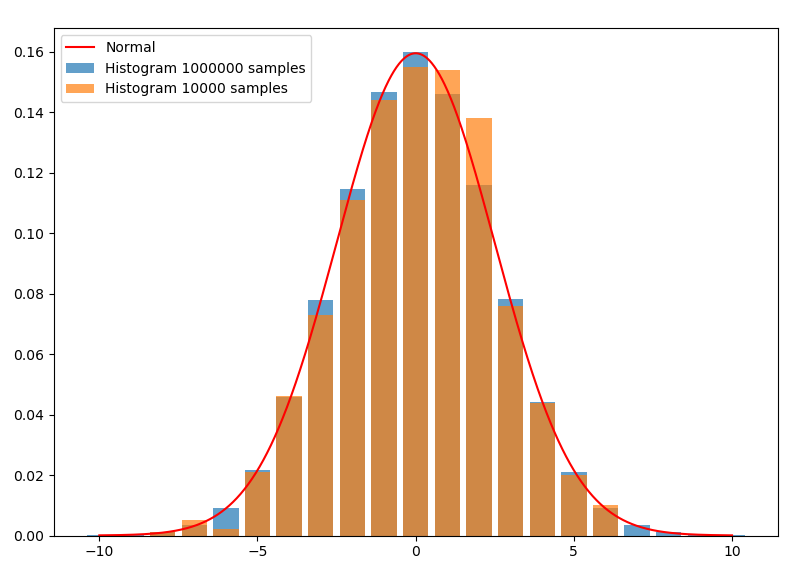
　　這裡的直方圖離散地取了21個相互無交集的區間：$[x-0.5,x+0.5), x=-10,-9,…,10$，單邊間隔$h=0.5$。$h>0$在核函數估計中通常稱作頻寬，或窗口。每個長條的面積就是樣本在這個區間內的頻率。如果用頻率當做概率，則面積除以區間寬度後的高，就是擬合出的在這個區間內的平均概率密度。因為這裡取的區間寬度是1，所以高與面積在數值上相同，使得長條的頂端正好與密度函數曲線相契合。如果將區間中的$x$取成任意值，就可以擬合出實數域內的概率密度（其中$N_x$為樣本$x_iin [x-h,x+h),i=1,…,N$的樣本數）：

$displaystylehat{f}(x)=frac{N_x}{N}cdotfrac{1}{2h}$

　　這就已經是核函數估計的一種了。顯然，抽樣越多，這個平均概率密度能擬合得越好，正如藍條中上方几乎都與曲線契合，而橙色則稂莠不齊。另外，如果抽樣數$Nto infty$，對$h$取極限$hto 0$，擬合出的概率密度應該會更接近真實概率密度。但是，由於抽樣的數量總是有限的，無限小的$h$將導致只有在抽樣點處，才有頻率$1/N$，而其它地方頻率全為0，所以$h$不能無限小。相反，$h$太大的話又不能有效地將抽樣量用起來。所以這兩者之間應該有一個最優的$h$，能充分利用抽樣來擬合概率密度曲線。容易推理出，$h$應該和抽樣量$N$有關，而且應該與$N$成反比。

核函數估計

　　為了便於拓展，將擬合概率密度的式子進行變換：

$displaystylehat{f}(x)=frac{N_x}{2hN} = frac{1}{hN}sumlimits_{i=1}^{N}begin{cases}1/2& x-hle x_i < x+h\ 0& else end{cases}$

$displaystyle = frac{1}{hN}sumlimits_{i=1}^{N}begin{cases} 1/2,& -1le displaystylefrac{x_i-x}{h} < 1\ 0,& else end{cases}$

 $displaystyle = frac{1}{hN}sumlimits_{i=1}^{N}displaystyle K(frac{x_i-x}{h}),;; where ; K(x) =begin{cases} 1/2,& -1le x < 1\ 0,& else end{cases}$

　　得到的$K(x)$就是uniform核函數（也又叫方形窗口函數），這是最簡單最常用的核函數。形象地理解上式求和部分，就是樣本出現在$x$鄰域內部的加權頻數（因為除以了2，所以所謂“加權”）。核函數有很多，常見的還有高斯核函數（高斯窗口函數），即：

$displaystyle K(x) = frac{1}{sqrt{2pi}}e^{-x^2/2}$

　　各種核函數如下圖所示：

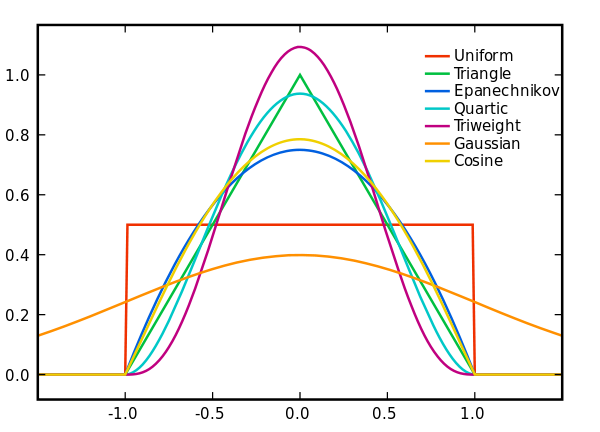
核函數的條件

　　並不是所有函數都能作為核函數的，因為$hat{f}(x)$是概率密度，則它的積分應該為1，即：

$displaystyleintlimits_{R}hat{f}(x) dx = intlimits_{R}frac{1}{hN}sumlimits_{i=1}^{N} K(frac{x_i-x}{h})dx =frac{1}{hN}sumlimits_{i=1}^{N} int_{-infty}^{infty} K(frac{x_i-x}{h})dx$

　　令$displaystyle t = frac{x_i-x}{h}$

$displaystyle =frac{1}{N}sumlimits_{i=1}^{N} int_{infty}^{-infty} -K(t)dt$

$displaystyle=frac{1}{N}sumlimits_{i=1}^{N} int_{-infty}^{infty} K(t)dt=1$

　　因積分部分為定值，所以可得$K(x)$需要的條件是：

$displaystyleint_{-infty}^{infty} K(x)dx=1$

　　通常$K(x)$是偶函數，而且不能小於0，否則就不符合實際了。

頻寬選擇與核函數優劣

　　正如前面提到的，頻寬$h$的大小關係到擬合的精度。對於方形核函數，$Nto infty$時，$h$通常取收斂速度小於$1/N$的值即可，如$h=1/sqrt{N}$。對於高斯核，有證明指出$displaystyle h=left (  frac{4 hat{sigma}^5 }{3N} right )^{frac{1}{5}}$時，有較優的擬合效果（$hat{sigma}^2$是樣本方差）。具體的頻寬選擇還有更深入的演算法，具體問題還是要具體分析，就先不細究了。使用高斯核時，待擬合的概率密度應該近似於高斯分布那樣連續平滑的分布，如果是像均勻分布那樣有明顯分塊的分布，擬合的效果會很差。我認為原因應該是它將離得很遠的樣本也用於擬合，導致本該突兀的地方都被均勻化了。

　　Epanechnikov在均方誤差的意義下擬合效果是最好的。這也很符合直覺，越接近$x$的樣本的權重本應該越高，而且超出頻寬的樣本權重直接為0也是符合常理的，它融合了均勻核與高斯核的優點。

多維情況

　　對於多維情況，假設隨機變數$X$為$m$維（即$m$維向量），則擬合概率密度是$m$維的聯合概率密度：

$displaystyle hat{f}(x)= frac{1}{h^mN}sumlimits_{i=1}^{N}displaystyle K(frac{x_i-x}{h})$

　　其中的$K(x)$也變成了$m$維的聯合概率密度。另外，既然$displaystylefrac{1}{N}sumlimits_{i=1}^{N} K(frac{x_i-x}{h})$代表的是概率，$m$維的概率密度自然是概率除以$h^m$而不是$h$。

實驗擬合情況