關於 JavaScript 的 精度丟失 與 近似舍入
- 2020 年 4 月 5 日
- 筆記
一、背景
最近做 dashborad 圖表時,涉及計算小數且四捨五入精確到 N 位。後發現 js 算出來的結果跟我預想的不一樣,看來這裡面並不簡單……
二、JS 與 精度
1、精度處理
首先明確兩點:
- 1、小數才會涉及精度的概念
- 2、小數的(存儲和)運算涉及 JS 的
精度處理
在現實中,我們運算小數,不會出現任何問題。但是 JS (程式語言)里,卻不是這樣。
2、精度丟失
例如,在 JS 里執行:
0.1 + 0.2 0.30000000000000004 0.3 - 0.1 0.19999999999999998 0.1 * 0.1 0.010000000000000002 0.3 / 0.1 2.9999999999999996 可以看出,JS 運算小數的結果,並不是我們預想的那樣。這就是精度丟失的問題。
(1)問:精度丟失會引發什麼問題?
答:
- 1、讓判斷等於(
===)的邏輯出錯。比如讓0.1 + 0.2 === 0.3為false - 2、讓本來可以預想到的結果精度變的特別大,小數點後位數特別長。比如若要前端顯示,會特別難看。
(2)問:為什麼會出現精度丟失?
答:這跟浮點數在電腦內部(用二進位存儲)的表示方法有關。
JS 採用 IEEE 754 標準的 64 位雙精度浮點數表示法,這個標準是20世紀80年代以來最廣泛使用的浮點數運算標準,為許多CPU與浮點運算器所採用,也被很多語言如 java、python 採用。
這個標準,會讓絕大部分的十進位小數都不能用二進位浮點數來精確表示(事實上,根本沒有什麼標準可以精確表示浮點數)。一般情況下,你輸入的十進位小數僅由實際存儲在電腦中的近似的二進位浮點數表示。
然而,許多語言在處理的時候,在一定誤差範圍內(通常極小)會將結果修正為正確的目標數字,而不是像 JS 一樣將存在誤差的真實結果轉換成最接近的小數輸出。
具體原理可以看《浮點數的二進位表示 —— 阮一峰》,這裡不贅述了。
(3)問:怎麼避免精度丟失?
方法一:中途變成整數來計算
比如我們要計算 0.1 + 0.2,就先把數字全部乘以 10 使之變成整數,再相加,最後把結果除以 10。
因為整數是不會出現精度丟失的問題。(況且整數根本就沒有精度)
其實很多第三方的庫,原理也是用的這個。
方法二:使用第三方庫
- Math.js
- decimal.js
- big.js
- bignumber.js
方法三:使用 toFixed() 函數(推薦)
console.log(parseFloat((0.3 + 0.1).toFixed(1))) // 0.4 注意:toFixed() 最好跟 parseFloat() 搭配使用。因為 toFixed 返回的是字元串。
問:toFixed() 為什麼要返回字元串,而不是小數?【重點】
答:因為 JavaScript 的數據類型,關於數字的只有 number 類型(不像 C 語言 or 資料庫等還分 int、float、double),而對於 number 類型來說, 會忽略前置0和小數點後的後置0(比如 001 是 1; 1.1000 是 1.1)。
在下面還會繼續介紹
toFixed()的關於四捨五入的特性。
三、JS 與 近似計算方法
在上面提到的:
- 精度計算
- 精度丟失
都會有可能讓精度發生變化(即小數點後位數變化)。如果我們需要統一精度,那就需要用到近似(計算)方法。
1、四捨五入
(1)規則
四捨五入是最常見的近似計算方法,具體規則顧名思義,不贅述了。
(2)Math.round()
給定數字的值四捨五入到最接近的整數。
Math.Round(2.4) // 2 Math.Round(2.5) // 3 (3)_.round() —— lodash
給定數字的值四捨五入到最接近的數(可以是小數)。
lodash 的這個方法,其實我看了源碼,底層也是調用的 Math.round(),只是加了一些額外功能,比如第二個參數,可以指定四捨五入的精度。
const _ = require('lodash'); _.round(1.04, 1) //1 _.round(1.05, 1) //1.1 (4)四捨五入真的公平嗎?【重點】
因為自己很小的時候就在學校學到了四捨五入,一直想當然的認為四捨五入是公平的,等到現在細想的時候,才發現,真的不公平。
例如,想像一個場景,你的餘額寶,每天會自動結算利息,但是可能(按照利息規則)算出來的值的小數有很多位,假設支付寶只支援到角,那麼支付寶系統幫你記賬的時候,肯定會給你近似計算,如果他用的是四捨五入的方法:
const _ = require('lodash'); console.log(_.round(1.01, 1)) //1 (我虧了0.01) console.log(_.round(1.02, 1)) //1 (我虧了0.02) console.log(_.round(1.03, 1)) //1 (我虧了0.03) console.log(_.round(1.04, 1)) //1 (我虧了0.04) console.log(_.round(1.05, 1)) //1.1 (我賺了了0.05) console.log(_.round(1.06, 1)) //1.1 (我賺了0.04) console.log(_.round(1.07, 1)) //1.1 (我賺了0.03) console.log(_.round(1.08, 1)) //1.1 (我賺了0.02) console.log(_.round(1.09, 1)) //1.1 (我賺了0.01) 首先,1 塊錢整和 2 塊錢整可以不用考慮,其次,如果假設 1.01 到 1.09 這 9 個數出現的概率一致。那麼最後支付寶肯定要虧本,因為 1.05 劃分到 1.1 是不公平的。
也可以畫一個數軸來體現:
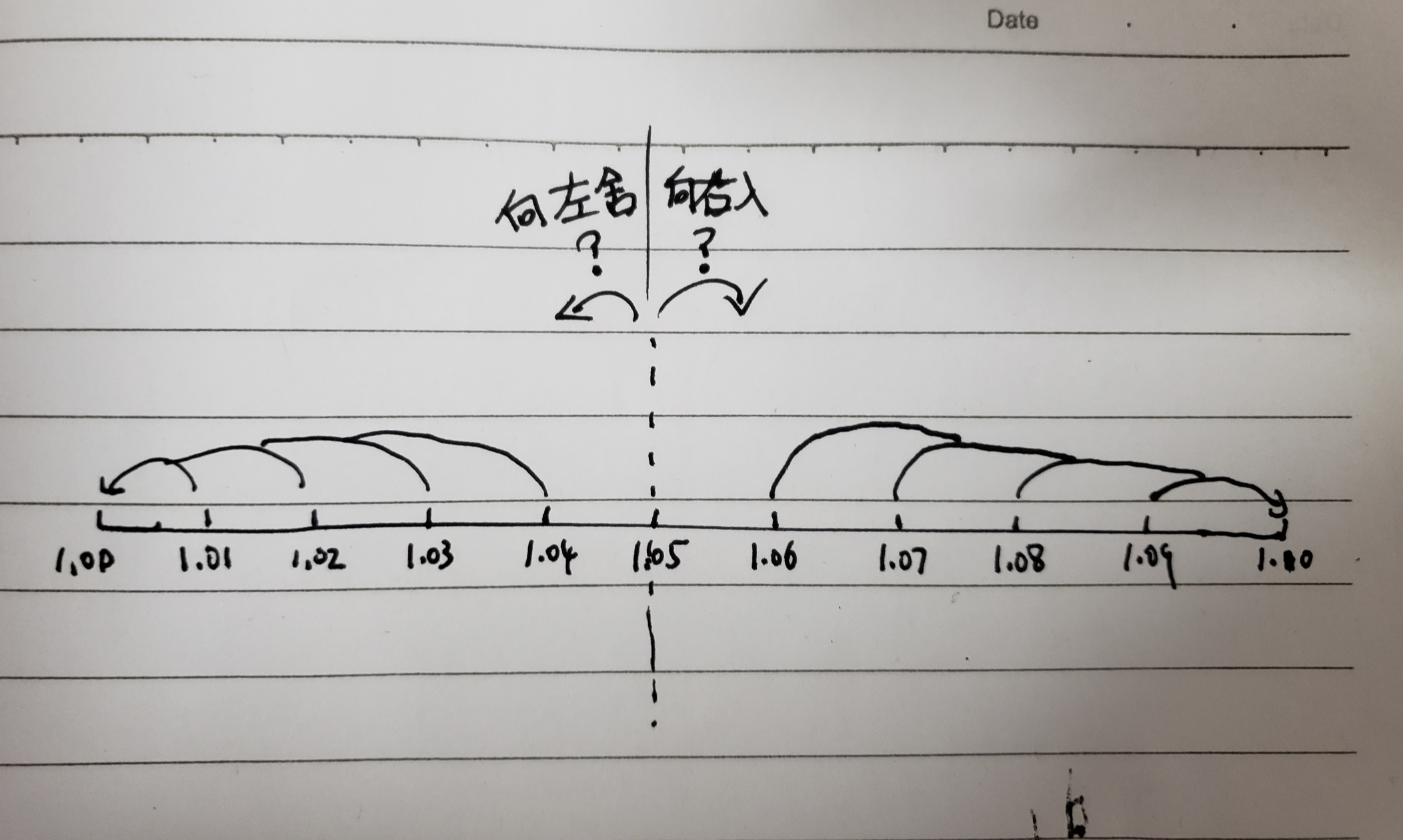
那麼如何做到更公平的近似計算呢?可以用下面介紹的銀行家舍入。
2、銀行家舍入
國際通行的是 銀行家舍入(Banker’s rounding)演算法 。
是 IEEE 規定的舍入標準。因此所有符合 IEEE 標準的語言都應該是採用這一規則的。
(1)規則
銀行家舍入又稱四捨六入五取偶(又稱四捨六入五留雙)法。
所以規則就是:四捨六入五考慮,五後非空就進一,五後為空看奇偶,五前為偶應捨去,五前為奇要進一。
關鍵就是「五後為空看奇偶」,因為如果是舍入位是5,無論是舍還是入都不公平,那就交給它前一位的奇偶性來判斷,因為奇偶性分布概率是公平的。
當然只能說銀行家舍入演算法比四捨五入演算法更科學,而不能說它就是絕對正確,而四捨五入就是錯誤的,因為這些結果都是基於統計數據產生的,前提就是這些數據搖符合隨機性分布的要求。
(2)使用
目前 JS 上原生不支援,如果想使用:
- 1、自己實現
- 2、使用第三方 npm 包,如 bankers-rounding
3、toFixed
toFixed() 部分符合銀行家舍入的規則。
(1)四捨六入
符合
(2)五後非空就進一
符合
(3)五後為空看奇偶,五前為偶應捨去,五前為奇要進一
部分符合
// //toFixed結果 //銀行家舍入結果 console.log(1.05.toFixed(1)) //1.1(+0.05) 1.0(-0.05) console.log(1.15.toFixed(1)) //1.1(-0.05) 1.2(+0.05) console.log(1.25.toFixed(1)) //1.3(+0.05) 1.2(-0.05) console.log(1.35.toFixed(1)) //1.4(+0.05) 1.4(+0.05) console.log(1.45.toFixed(1)) //1.4(-0.05) 1.4(-0.05) console.log(1.55.toFixed(1)) //1.6(+0.05) 1.6(+0.05) console.log(1.65.toFixed(1)) //1.6(-0.05) 1.6(-0.05) console.log(1.75.toFixed(1)) //1.8(+0.05) 1.8(+0.05) console.log(1.85.toFixed(1)) //1.9(+0.05) 1.8(-0.05) console.log(1.95.toFixed(1)) //1.9(-0.05) 2.0(+0.05) // //總計(+0.1) //總計(0) 可以看出 toFixed 肯定是不遵守四捨五入的,但是也跟銀行家舍入演算法有出入。(具體為什麼是這樣的計算方法,鄙人並不是弄清楚,待寫)
4、其他 近似計算 函數
- Math.ceil():向上舍入(取整)
- Math.floor():向下舍入(取整)
- 等等……

