python實現十大經典排序演算法
- 2020 年 4 月 4 日
- 筆記
Python實現十大經典排序演算法
程式碼最後面會給出完整版,或者可以從我的Githubfork,想看動圖的同學可以去這裡看看;
小結:
- 運行方式,將最後面的程式碼copy出去,直接python sort.py運行即可;
- 程式碼中的健壯性沒有太多處理,直接使用的同學還要檢查檢查;
- 對於希爾排序,gap的選擇至關重要,需要結合實際情況更改;
- 在我的測試中,由於待排序數組很小,長度僅為10,且最大值為10,因此計數排序是最快的,實際情況中往往不是這樣;
- 堆排序沒來得及實現,是的,就是懶了;
- 關鍵在於理解演算法的思路,至於實現只是將思路以合理的方式落地而已;
- 推薦大家到上面那個鏈接去看動圖,確實更好理解,不過讀讀程式碼也不錯,是吧;
- 分治法被使用的很多,事實上我不太清楚它背後的數學原理是什麼,以及為什麼分治法可以降低時間複雜度,有同學直到麻煩評論區告訴我一下哈,多謝;
運行圖
由於數組小,且範圍在1到10之間,這其實對於計數排序這種非比較類演算法是比較友好的,因為沒有多大的空間壓力,因此計數排序速度第一很容易理解,而之所以選擇、插入比希爾歸併要快,主要還是因為問題規模本身太小,而我的分治法的實現是基於遞歸,因此看不出分治法的優勢,事實上如果對超大的數組進行排序的話,這個區別會體現出來;
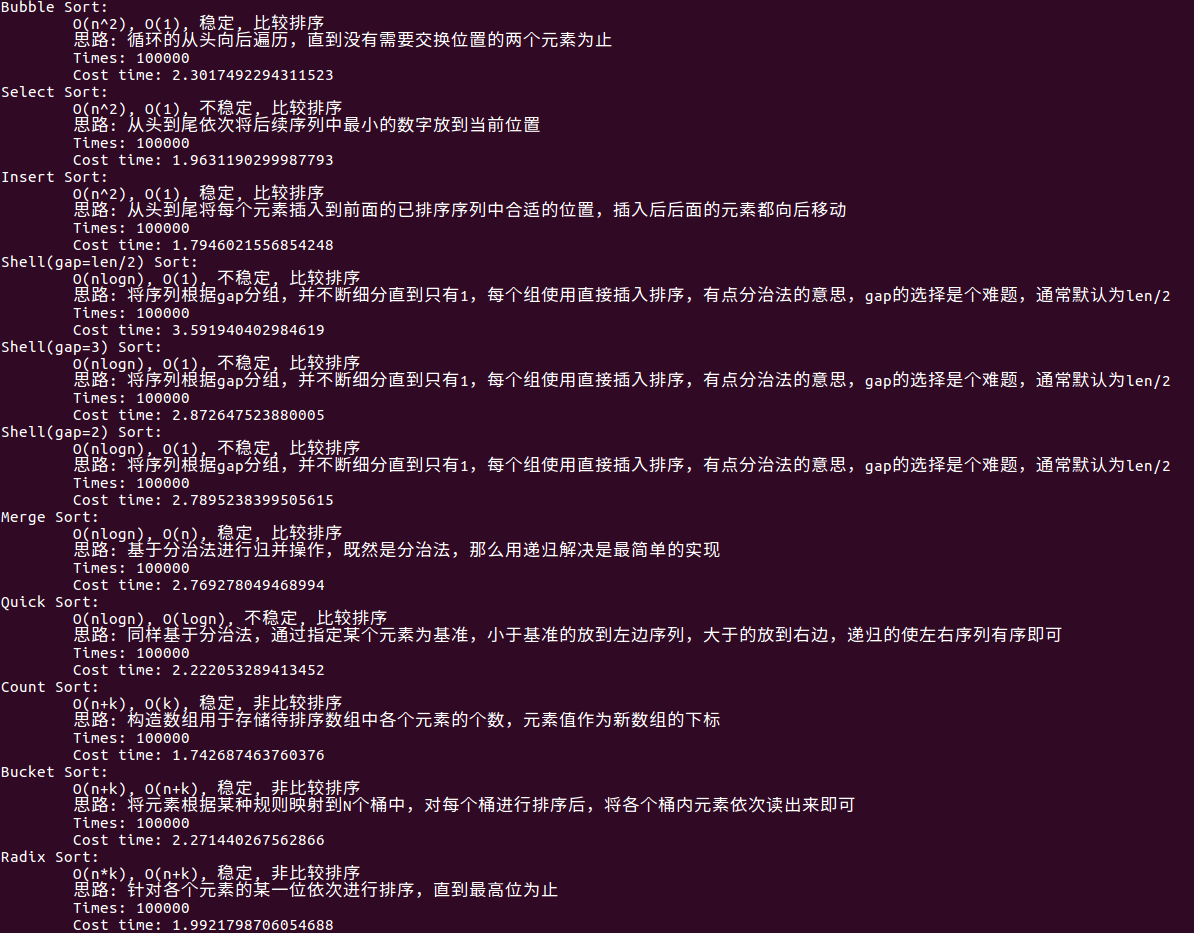
完整程式碼
可以看到,全部程式碼不包括測試程式碼總共才170行,這還包括了空行和函數名等等,所以本身演算法實現是很簡單的,大家還是要把注意力放在思路上;
import sys,random,time def bubble(list_): running = True while running: have_change = False for i in range(len(list_)-1): if list_[i]>list_[i+1]: list_[i],list_[i+1] = list_[i+1],list_[i] have_change = True if not have_change: break return list_ def select(list_): for i in range(len(list_)-1): min_idx = i for j in range(i,len(list_)): if list_[min_idx]>list_[j]: min_idx = j list_[i],list_[min_idx] = list_[min_idx],list_[i] return list_ def insert(list_): for i in range(1,len(list_)): idx = i for j in range(i): if list_[j]>list_[idx]: idx = j break if idx != i: tmp = list_[i] list_[idx+1:i+1] = list_[idx:i] list_[idx] = tmp return list_ def shell(list_,gap=None): ''' gap的選擇對結果影響很大,是個難題,希爾本人推薦是len/2 這個gap其實是間隙,也就是間隔多少個元素取一組的元素 例如對於[1,2,3,4,5,6,7,8,9,10] 當gap為len/2也就是5時,每一組的元素都是間隔5個的元素組成,也就是1和6,2和7,3和8等等 ''' len_ = len(list_) gap = int(len_/2) if not gap else gap while gap >= 1: for i in range(gap): list_[i:len_:gap] = insert(list_[i:len_:gap]) gap = int(gap/2) return list_ def merge(list_): ''' 歸併排序的遞歸實現 思路:將數據劃分到每兩個為一組為止,將這兩個排序後範圍,2個包含2個元素的組繼續排序為1個4個元素的組, 直到回溯到整個序列,此時其實是由兩個有序子序列組成的,典型的遞歸問題 ''' if len(list_)<=1: return list_ if len(list_)==2: return list_ if list_[0]<=list_[1] else list_[::-1] len_ = len(list_) left = merge(list_[:int(len_/2)]) right = merge(list_[int(len_/2):]) tmp = [] left_idx,right_idx = 0,0 while len(tmp)<len(list_): if left[left_idx]<=right[right_idx]: tmp.append(left[left_idx]) left_idx+=1 if left_idx==len(left): tmp += right[right_idx:] break else: tmp.append(right[right_idx]) right_idx+=1 if right_idx==len(right): tmp += left[left_idx:] break return tmp def quick(list_): ''' 快速排序:基於分治法,選定某個元素為基準,對剩餘元素放置到基準的左側和右側,遞歸這個過程 ''' if len(list_)<=1: return list_ if len(list_)==2: return list_ if list_[0]<=list_[1] else list_[::-1] base_idx = int(len(list_)/2) base = list_[base_idx] left = [] right = [] for i in range(len(list_)): if i != base_idx: if list_[i] <= base: left.append(list_[i]) else: right.append(list_[i]) return quick(left)+[base]+quick(right) def count(list_): ''' 需要元素都是整型 ''' min_,max_ = list_[0],list_[0] for i in range(1,len(list_)): if list_[i]<min_: min_ = list_[i] if list_[i]>max_: max_ = list_[i] count_list = [0]*(max_-min_+1) for item in list_: count_list[item-min_] += 1 list_ = [] for i in range(len(count_list)): for j in range(count_list[i]): list_.append(i+min_) return list_ def heap(list_): ''' ''' pass def bucket(list_): ''' 每個桶使用選擇排序,分桶方式為最大值除以5,也就是分為5個桶 桶排序的速度取決於分桶的方式 ''' bucket = [[],[],[],[],[]] # 注意長度為5 max_ = list_[0] for item in list_[1:]: if item > max_: max_ = item gap = max_/5 # 對應bucket的長度 for item in list_: bucket[int((item-1)/gap)].append(item) for i in range(len(bucket)): bucket[i] = select(bucket[i]) list_ = [] for item in bucket: list_ += item return list_ def radix(list_): ''' 基數排序:對數值的不同位數分別進行排序,比如先從個位開始,然後十位,百位,以此類推; 注意此處程式碼是假設待排序數值都是整型 ''' max_ = list_[0] for item in list_[1:]: if item > max_: max_ = item max_radix = len(str(max_)) radix_list = [[],[],[],[],[],[],[],[],[],[]] # 對應每個位上可能的9個數字 cur_radix = 0 while cur_radix<max_radix: base = 10**cur_radix for item in list_: radix_list[int(item/base)%10].append(item) list_ = [] for item in radix_list: list_ += item radix_list = [[],[],[],[],[],[],[],[],[]] # 對應每個位上可能的9個數字 cur_radix += 1 return list_ def test(name,sort_func,times,info,idea,*param): list_ = [1,2,3,4,5,6,7,8,9,10] print(name+' Sort:') print('t'+info) print('t'+idea) print('tTimes: '+str(times)) start_time = time.time() for i in range(times): random.shuffle(list_) #print('tInput: '+str(list_)) list_ = sort_func(list_) if len(param)<=0 else sort_func(list_,param[0]) #print('tOutput: '+str(list_)) #print('t'+str(list_)) print('tCost time: '+str(time.time()-start_time)) if __name__ == "__main__": test('Bubble',bubble,100000,'O(n^2), O(1), 穩定, 比較排序','思路: 循環的從頭向後遍歷,直到沒有需要交換位置的兩個元素為止') test('Select',select,100000,'O(n^2), O(1), 不穩定, 比較排序','思路: 從頭到尾依次將後續序列中最小的數字放到當前位置') test('Insert',insert,100000,'O(n^2), O(1), 穩定, 比較排序','思路: 從頭到尾將每個元素插入到前面的已排序序列中合適的位置,插入後後面的元素都向後移動') test('Shell(gap=len/2)',shell,100000,'O(nlogn), O(1), 不穩定, 比較排序','思路: 將序列根據gap分組,並不斷細分直到只有1,每個組使用直接插入排序,有點分治法的意思,gap的選擇是個難題,通常默認為len/2') test('Shell(gap=3)',shell,100000,'O(nlogn), O(1), 不穩定, 比較排序','思路: 將序列根據gap分組,並不斷細分直到只有1,每個組使用直接插入排序,有點分治法的意思,gap的選擇是個難題,通常默認為len/2',3) test('Shell(gap=2)',shell,100000,'O(nlogn), O(1), 不穩定, 比較排序','思路: 將序列根據gap分組,並不斷細分直到只有1,每個組使用直接插入排序,有點分治法的意思,gap的選擇是個難題,通常默認為len/2',2) test('Merge',merge,100000,'O(nlogn), O(n), 穩定, 比較排序','思路: 基於分治法進行歸併操作,既然是分治法,那麼用遞歸解決是最簡單的實現') test('Quick',quick,100000,'O(nlogn), O(logn), 不穩定, 比較排序','思路: 同樣基於分治法,通過指定某個元素為基準,小於基準的放到左邊序列,大於的放到右邊,遞歸的使左右序列有序即可') # test('Heap',heap,100000,'O(nlogn), O(1), 不穩定, 比較排序','思路: 利用堆的性質構建完全二叉樹') test('Count',count,100000,'O(n+k), O(k), 穩定, 非比較排序','思路: 構造數組用於存儲待排序數組中各個元素的個數,元素值作為新數組的下標') test('Bucket',bucket,100000,'O(n+k), O(n+k), 穩定, 非比較排序','思路: 將元素根據某種規則映射到N個桶中,對每個桶進行排序後,將各個桶內元素依次讀出來即可') test('Radix',radix,100000,'O(n*k), O(n+k), 穩定, 非比較排序','思路: 針對各個元素的某一位依次進行排序,直到最高位為止') # print(heap([4,6,8,3,5,10,9,2,1,7])) 最後
大家可以到我的Github上看看有沒有其他需要的東西,目前主要是自己做的機器學習項目、Python各種腳本工具、有意思的小項目以及Follow的大佬、Fork的項目等:
https://github.com/NemoHoHaloAi
