系列篇|結構光——格雷碼解碼方法
- 2020 年 4 月 3 日
- 筆記
作者:書涵
Date:2020-03-16
來源:系列篇|結構光——格雷碼解碼方法
Date:2020-03-16
來源:系列篇|結構光——格雷碼解碼方法
格雷碼是一種特殊的二進位碼,在結構光三維視覺中,常常被用於編碼。比起我們常見的二進位碼,格雷碼具有相鄰數字的編碼只有一位不同的優點,這個優點對於解碼而言十分重要,可以減少光解碼的錯誤率。下面我們可以看下如何對結構光用格雷碼編碼,並如何對編碼的結構光進行解碼。
以5位格雷碼為例,5位格雷碼可以對32個像素位置進行編碼,由之前的文章可以知道,我們在計算結構光三維重建時,只需要對結構光圖片的一個方向編碼,以常見的列格雷碼為例,如圖所示是5位列格雷碼編碼圖片集。

圖中我們對每個像素點進行了格雷碼編碼,每一張圖片都代表了格雷碼的某一位,以圖片第1列為例,其格雷碼編碼為00001,則前4張圖片中第一列的的格雷碼編碼的條紋都是黑色,代表0,而最後一張圖片第一列的格雷碼編碼是白色,代表1.
格雷碼的解碼很簡單,只要把投影的格雷碼結構光再還原回十進位數字,我們就能知道相機中的像素點(uc,vc)對應的是投影圖片的哪一列(up)了。想要得到一個好的三維重建結果,主要是對相機捕捉到的結構光進行準確的二值化操作,使得相機圖片中每個像素點都能夠正確解碼。
常見的二值化操作有很多,最簡單的是設一個全局灰度閾值,對灰度值高於閾值的像素點置1,對灰度值低於閾值的像素點置0。 或者利用局部自適應閾值對圖片進行二值化操作等·。常見的利用每個像素點周邊灰度資訊的二值化操作,往往不能夠滿足格雷碼結構光解碼的二值化需求。因為使用結構光的環境往往是未知且複雜的。比如同樣的結構光光強照在黑色物體表面的亮度比照射在白色物體表面的亮度要低。這意味著同樣的光條紋在不同物體上獲取的灰度值不同。由於不能提前預知環境中的物體表面資訊,僅僅靠簡單的利用像素點及其周周圍灰度值的分布得出該像素點當前是來自結構光的亮條紋還是暗條紋是及其不準確的。
雖然由於環境光,以及物體表面材質的原因,一幅影像中像素的亮度(灰度值)通常是不均勻的,無法直接利用一張圖片呈現的灰度資訊對結構光解碼,但是我們可以利用結構光系列圖片來幫助獲取像素點當前是亮條紋還是暗條紋的資訊。以上圖的格雷碼編碼為例,一個5位的格雷碼編碼需要投影5張結構光圖片,假設有一個編碼為 11011的格雷碼條紋打在物體表面上,,在連續投影的5張格雷碼圖片中,物體表面被編碼照射的位置既經歷過暗條紋(編碼為0)又經歷過亮條紋(編碼為1)。不過由於每張格雷碼編碼圖片的光源編碼不同,而且結構光光源在物體表面上形成的漫反射不同,當結構光編碼圖片不一樣時,即使是同樣經歷亮條紋照射,該位置的亮度(灰度值)也是不同的。總的來說,對於同一個位置,可以近似認為其被亮條紋照射到的亮度總是高於其被暗條紋照射到的亮度。那麼對於一個像素點在一張圖片中的二值化可以用如下方法。
首先找到像素點在系列格雷碼圖片中最大的灰度值,記為Imax,並找到該像素點在系列格雷碼圖片中最小的灰度值,記為Imin。對於每張圖片,我們可以這樣計算,
In = (I-Imin)/(Imax-Imin)
其中I是該像素點在當前圖片下的亮度,In可以看做是被歸一化(normalize)後的灰度值,顯然In的取值範圍是[0,1]的。由上述公式可以看出,如果該像素點當前經歷的是暗條紋,其值會接近最小的灰度值,In接近0,反之,In會接近1, 於是我們可以設計一個閾值,比如0.5,即當In大於0.5時,我們認為其值是偏亮的,此時像素經歷的是亮條紋編碼,反之,如果In小於0.5時,該像素此時經歷的是暗條紋編碼。值得注意的是,這個方法對於編碼全為0的點,或者編碼全為1的點,會有影響,因為編碼全0的點和編碼全1的點不會同時經歷明暗變化。解決方法是避開這個編碼,或者額外投圖片讓所有編碼位置都能經歷全0或者全1的過程。
上述方法的前提是近似認為被亮條紋照射到的亮度總是高於該位置被暗條紋照射到的亮度。實際上這個假設成立的前提是物體間沒有漫反射,以及投影投射的光之間不會互相干擾。在一些特殊的位置,是有可能物體在經歷亮條紋時其亮度值比其經歷暗條紋時要暗。因為每張格雷碼圖片總體的光分布是不一樣的,如上圖的第一張和最後一張,第一張光主要分布在右邊半邊,而最後一張條紋光很細,是明暗相間的。不一樣的格雷碼圖片的光強分布,會造成物體間漫反射的光強不一樣,導致其經歷暗條紋時周圍物體間漫反射到的光遠大於結構光光源發出來的光。實際上這是有可能的,比如該像素點處於某個物體對的陰影部分,一般情況下這樣的點是沒有光變化的,因為結構光本身無法直射到該位置,但是因為其周邊物體漫反射的光有可能導致這個位置的光強發生劇烈變化。出現該位置經歷暗條紋時光強比經歷亮條紋時還要強。為了解決這類特殊的點,論文[2] 給出其思路如下:

如圖所示,我們可以對每幅格雷碼編碼的條紋做一個逆向圖,把原來編碼條紋中的1的位置變為0,0的位置成1。這樣我們把每一幅編碼圖片變成了一對編碼圖. 我們可以通過比較一對編碼圖中每個像素的灰度差值來判斷其值為0還是為1。這個很容易理解,因為如果編碼是亮條紋,則其逆向編碼是暗條紋,則圖片上編碼是亮條紋的時候對應的點比編碼是暗條紋(逆向)的時候對應的像素點更亮,即灰度值更高。反之亦然, 這樣就可以簡單地對相機圖片上的結構光條紋解碼了。
這個思路很簡單,對大部分相機圖片上的點,這樣的解碼效果就足夠好了。但是仍然不能解決上述提到的問題。對於部分點,其經歷暗條紋時仍舊可能比經歷亮條紋時灰度值要更高。於是論文【2】在上述思路上,再增加了一部分想法,如果我們能求出當前灰度值中可能的來自結構光直接光源的成分的比例,就可以幫助我們辨別出該點是否經歷暗條紋或者亮條紋。具體計算規則如下:
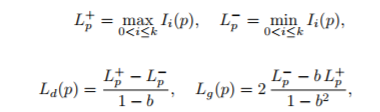
其中p指像素坐標,Lp+ 是像素在格雷碼系列圖中灰度最大值,Lp-是像素在格雷碼系列圖中灰度最小值。Ld可以看作是該像素點來自直接光源的灰度值,Lg可以看作來自其他光源(物體間漫反射和環境光)等的光源的灰度值。對於大部分情況,顯然來自投影光的光強較強,Ld>Lg。但是對於部分點Ld<Lg, 比如處於物體陰影處的點,又比如處於周圍反光物體較多點(來自周圍反光太強了)。這部分點就是我們要解決的點,通過下面的規則,可以很好的解決點的二值化問題:
對每個像素點p和其灰度值I,有如下二值化規則 其中m是一個比較小的常數閾值,I_inv是條紋結構光的逆向圖。
-
I<m 該點的二值化認為是不確定點
-
Ld>Lg 且滿足 I>I_inv 該點二值化為1
-
Ld>Lg 且滿足I <I_inv 該點二值化為0
-
I<Ld 且滿足I_inv>Lg 該點二值化為0
-
I>Lg 且滿足I_inv<Ld 該點二值化為1
不符合以上所有條件的點為不確定點
有了以上的二值化方法,格雷碼的編碼和解碼都不是什麼太大的問題,解碼後可以根據筆者之前文章提供的三維數據計算方法得到較為準確的物體三維資訊。
在文章的最後,筆者想討論下為什麼格雷碼編碼比一般的二進位編碼要好。我們知道格雷碼最大的優點是十進位相鄰數字編碼只相差一位。那為什麼這樣就比普通二進位編碼好呢?我們知道,解碼最容易出錯的點,往往是黑白相間的邊界點,相機拍攝到的黑白相間的邊界點往往是一個過渡灰度,很容易導致解碼錯誤,所以相鄰的數字間位數差別越多,其黑白相間的變化越多,自然出錯的概率也更大。對於這一點,其實有一個圖片很直觀感受到,如果我們對每個像素進行格雷碼編碼,那麼無論多少位編碼,在其編碼的最後一張圖片上,條紋通常是非常細的,如果是普通二進位編碼,其最後一張細條紋圖片是每個像素之間編碼都不一樣,對一幅圖片從左到右呈現010101…的變化,而如果用格雷碼編碼則會呈現0110011…的變化,明顯格雷碼編碼其投影條紋更粗,更不容易解碼出錯。
本文解碼方法參考論文:
[1] High-accuracy, high-speed 3D structured light imaging techniques and potential applications to intelligent robotics
[2] Robust Pixel Classification for 3D Modeling with Structured Light