5L-鏈表導論心法

2020 年 4 月 1 日
筆記

鏈表是比數組稍微複雜一點的數據結構，也是兩個非常重要與基本的數據結構。如果說數組是紀律嚴明排列整齊的「正規軍」那麼鏈表就是靈活多變的「地下黨」。

關注公眾號 MageByte，有你想要的精彩內容。

鏈表是一種物理存儲單元上非連續、非順序的存儲結構，數據元素的邏輯順序是通過鏈表中的指針鏈接次序實現的。鏈表由一系列結點（鏈表中每一個元素稱為結點）組成，結點可以在運行時動態生成。鏈表的節點由數據和一個或多個指針域組成。如果不考慮插入、刪除操作之前查找元素的過程，只考慮純粹的插入與刪除，那麼鏈表在插入和刪除操作上的演算法複雜 O(1)。

鏈表大集結

電影中我們看過，一個特務只知道自己上級、下級的資訊，地下黨通過這種單線聯絡的的方式靈活隱秘的傳遞著消息。鏈表家族也有多種分類，最簡單的單鏈表、循環鏈表、雙向鏈表、雙向循環鏈表。

底層數據結構與數組最大的區別，數組需要一塊連續的記憶體空間來存儲，而鏈表並不需要一塊連續的記憶體空間，它通過「指針」將一組零散的記憶體塊串聯起來使用。這就是地下黨靈活多變的本質原因，可隨時切換自己的上下級。

單鏈表

我們把記憶體塊稱為鏈表的「節點」，為了把所有分散的節點串連起來，每個節點除了存儲數據外，還需要記錄節點的下一個節點的地址，叫做「後繼指針 next」。

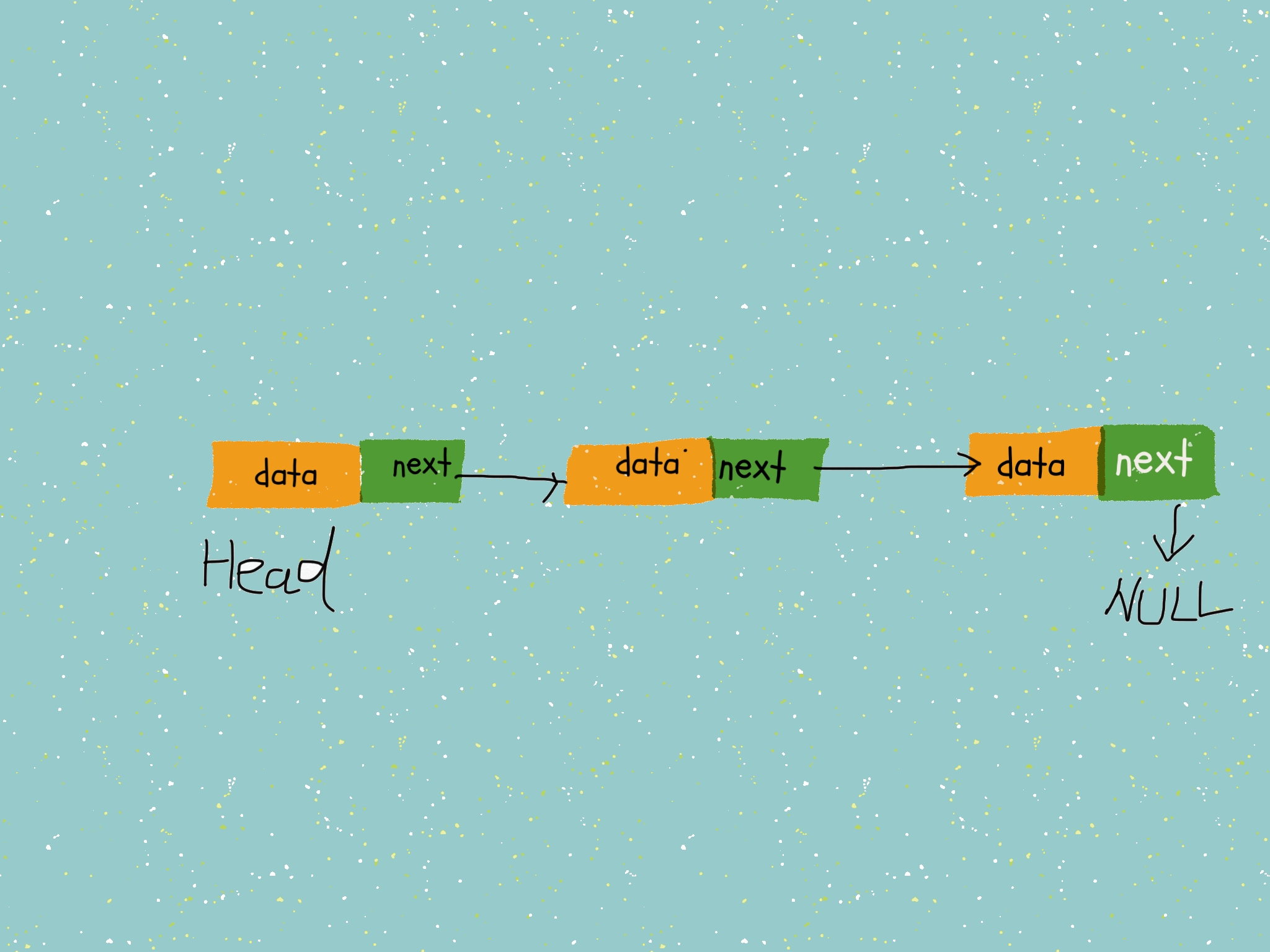
有兩個節點需要注意，分別是第一個節點「頭節點」和最後一個節點「尾節點」。頭結點記錄鏈表的基地址，這樣就可以遍歷得到整條鏈表數據，而尾節點的「next」只想一個空地址 NULL，代表這是最後一個節點。

鏈表的刪除與插入操作，只需要考慮相鄰節點的指針改變，所以時間複雜度是 O(1)。

有利就有弊，鏈表想要隨機訪問第 j 個元素，就沒有數組高效。鏈表的數據並不是連續存儲的，無法像數組一樣根據首地址和下標通過定址公式就可以計算出對應的 j 位置記憶體地址，需要根據指針一個一個節點的一次遍歷，直到查找到對應的節點。

這個就像地下黨組織，每個人只知道自己的後邊是誰，想要把消息傳到 k 特務，就需要從消息發布者開始通知他的下一級，直到 k 為止。所以隨機訪問的性能沒有數組好，時間複雜度是 O(n)。

插入節點

尾部插入

與數組類似，插入節點也可以分頭部插入、中部插入、尾部插入。尾部插入最簡單，把最後一個節點的「next」指針指向新插入的節點即可。

頭部插入

分為兩個步驟。

第一步，把新節點的「next」指針指向原先的頭節點。

第步，把新節點變為鏈表的頭節點。

中間插入

同樣分為兩個步驟。

把插入位置的節點前置節點的「next」指針指向指定插入的新節點。
將新節點的「next」指針指向前置節點的「next」指針原先所指定的節點。

刪除節點

單鏈表的刪除也分為三種情況。

頭部刪除
中部刪除
尾部刪除

尾部刪除最簡單，把倒數第二個節點的「next」指針指向 null，同時把要刪除的節點全都設置 null 讓垃圾收集器回收即可。

頭部刪除，把原先鏈表的頭節點的「next」節點設置成頭結點，並且把原來的頭結點設置 null 便於 gc 即可。

中間刪除，把要刪除的節點前置節點的「next」指針指向被刪除節點的「next」指針即可。

對於刪除與插入，只要我們畫下圖就很清晰了。

循環鏈表

循環鏈表是一種特殊的單鏈表。實際上，循環鏈表也很簡單。它跟單鏈表唯一的區別就在尾結點。我們知道，單鏈表的尾結點指針指向空地址，表示這就是最後的結點了。而循環鏈表的尾結點指針是指向鏈表的頭結點。從我畫的循環鏈表圖中，你應該可以看出來，它像一個環一樣首尾相連，所以叫作「循環」鏈表。

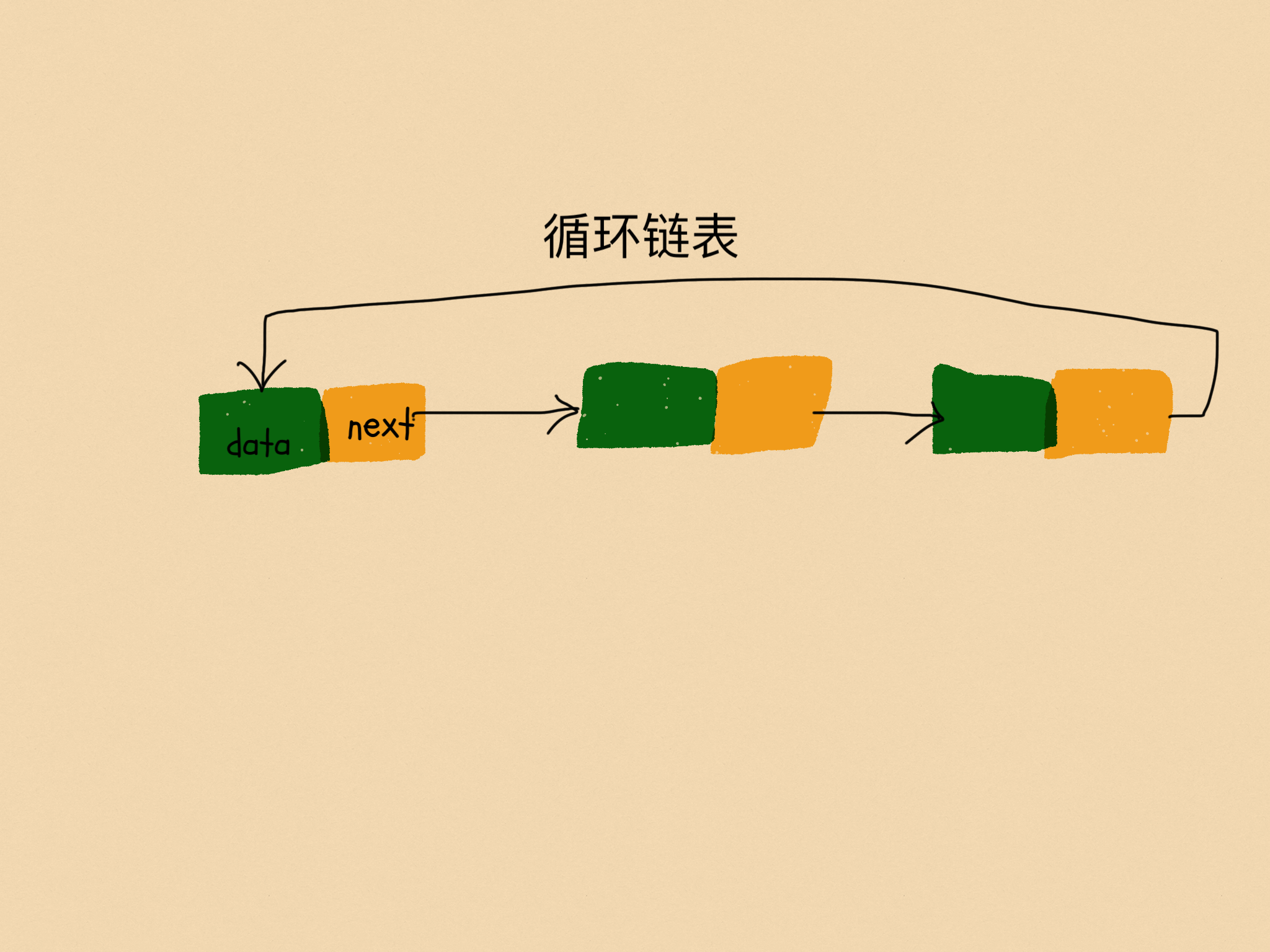
跟單鏈表差別不大，主要就是尾部節點遍歷到頭部節點方便。

雙向鏈表

實際開發中最常見的鏈表-雙向鏈表。Java 中的 LinkedList就是一個雙向鏈表。

單鏈表只有一個方向，每個節點只有一個後繼指針「next」指向下一個節點。雙向鏈表則是有兩個指針，每個節點分別有一個「next」指針指向後面節點和一個「prev」指針指向前置節點。

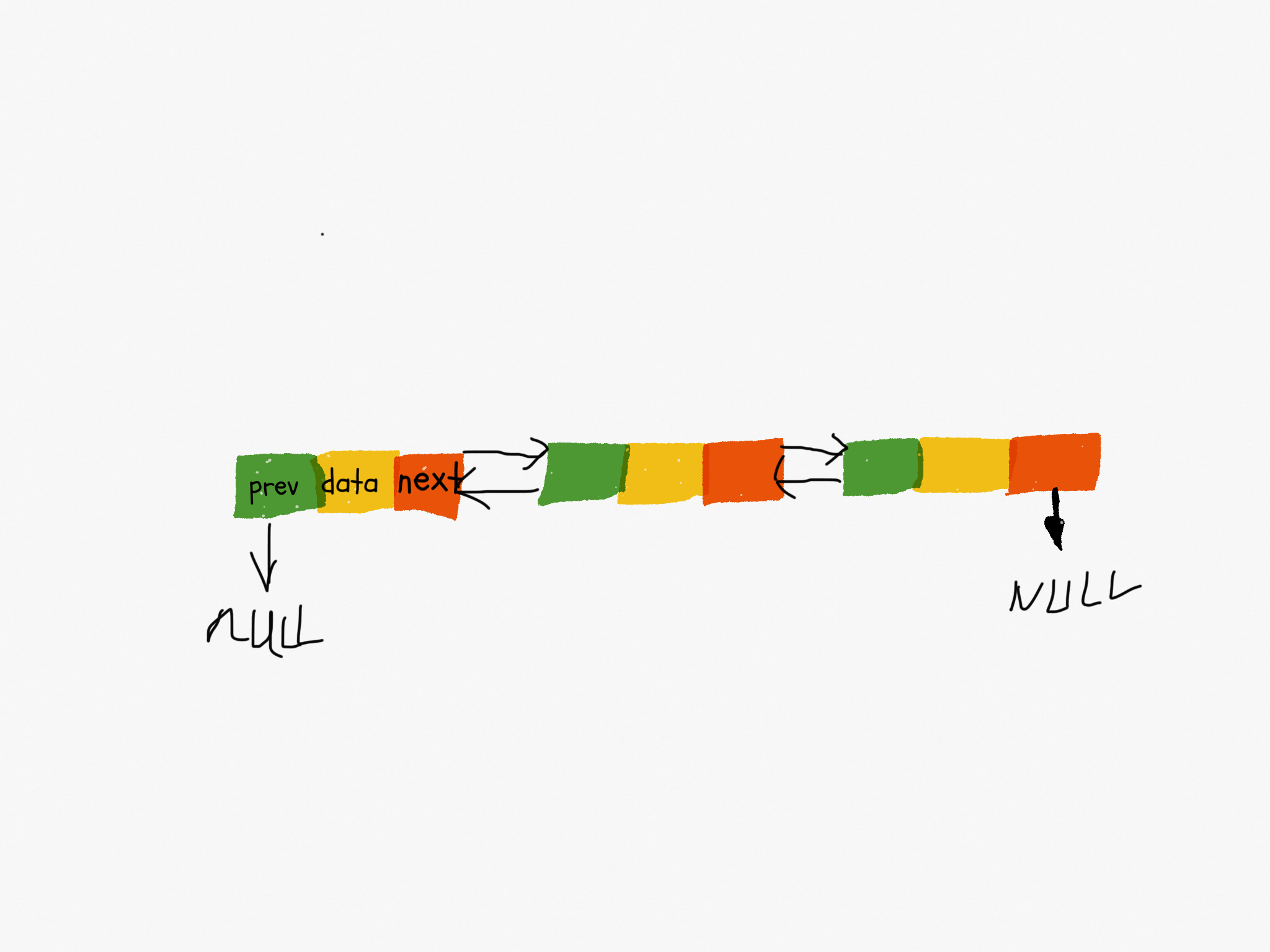
可以看出來，雙向鏈表需要額外的兩個空間存儲後繼節點和前驅節點地址。所以存儲同樣多的數據，雙向鏈表比單項鏈表佔用更多的空間，但是優勢則是可以雙向遍歷。

雙向鏈表可以支援在 O(1) 時間複雜度情況定位到前驅結點，正是這樣的特點，也使雙向鏈表在某些情況下的插入、刪除等操作都要比單鏈表簡單、高效。

之前我們說單項鏈表的刪除、插入時間複雜度是 O(1)了，那為啥這裡還說雙向鏈表的刪除、插入還能更高效呢？

從鏈表刪除一個元素，其實有兩種情況：

刪除「值等於給定的內容」的節點。
刪除給定指針指向的節點。

第一種情況，其實都一樣，不管是單項還是雙向都需要從頭節點遍歷比對找到要刪除的節點。

對於第二種情況，我們已經找到了要刪除的結點，但是刪除某個結點 q 需要知道其前驅結點，而單鏈表並不支援直接獲取前驅結點，所以，為了找到前驅結點，我們還是要從頭結點開始遍歷鏈表，直到 p->next=q，說明 p 是 q 的前驅結點。

但是對於雙向鏈表來說，這種情況就比較有優勢了。因為雙向鏈表中的結點已經保存了前驅結點的指針，不需要像單鏈表那樣遍歷。所以，針對第二種情況，單鏈表刪除操作需要 O(n) 的時間複雜度，而雙向鏈表只需要在 O(1) 的時間複雜度內就搞定了！

雙向循環鏈表

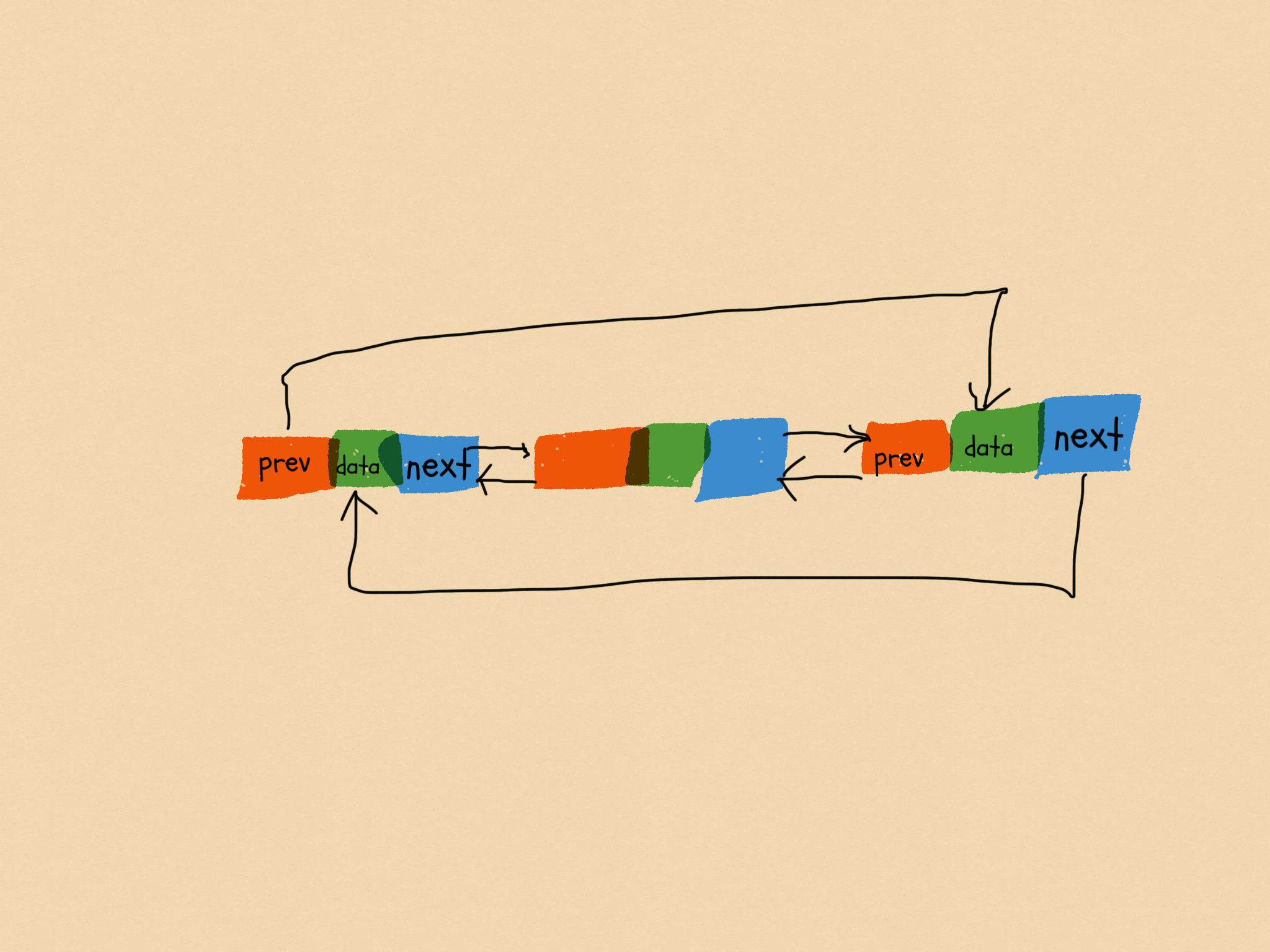
數組與鏈表性能比較

數組和鏈表都屬於線性的數據結構，用哪一個好呢？其實數據結構沒有絕對的好壞，各有千秋。

	查找	更新	刪除	插入
數組	O(1)	O(1)	O(n)	O(n)
鏈表	O(n)	O(1)	O(1)	O(1)

數組簡單易用，在實現上使用的是連續的記憶體空間，可以藉助 CPU 的快取機制，預讀數組中的數據，所以訪問效率更高。而鏈表在記憶體中並不是連續存儲，所以對 CPU 快取不友好，沒辦法有效預讀。

對鏈表進行頻繁的插入、刪除操作，還會導致頻繁的記憶體申請和釋放，容易造成記憶體碎片，如果是 Java 語言，就有可能會導致頻繁的 GC（Garbage Collection，垃圾回收）。

本文講解了鏈表的理論原理與知識，下一篇將程式碼實操擼一遍。

課後作業

如何基於鏈表實現一個 LRU 快取淘汰演算法？公眾號後台回復 LRU，可以獲取答案。

歡迎加群與我們討論分享，我們第一時間回饋。