機器學習3- 一元線性回歸+Python實現

• 2020 年 3 月 31 日
• 筆記

1. 線性模型

給定 (d) 個屬性描述的示例 (boldsymbol{x} = (x_1; x_2; …; x_d))，其中 (x_i) 為 (boldsymbol{x}) 在第 (i) 個屬性上的取值，線性模型（linear model）試圖學得一個通過屬性的線性組合來進行預測的函數，即：

使用向量形式為：

其中 (boldsymbol{w} = (w_1;w_2;…;w_d))，表達了各屬性在預測中的重要性。

2. 線性回歸

給定數據集 (D = lbrace(boldsymbol{x}_1,{y}_1), (boldsymbol{x}_2,{y}_2), …, (boldsymbol{x}_m,{y}_m)rbrace)，其中 (boldsymbol{x}_i = (x_{i1}; x_{i2}; …; x_{id}))，(y_i in mathbb{R})。線性回歸（linear regression）試圖學得一個能儘可能準確地預測真實輸出標記的線性模型，即：

2.1 一元線性回歸

先只考慮輸入屬性只有一個的情況，(D = lbrace({x}_1,{y}_1), ({x}_2,{y}_2), …, ({x}_m,{y}_m)rbrace)，(x_i in mathbb{R})。對離散屬性，若屬性值存在序（order）關係，可通過連續化將其轉化為連續值。

如」高度「屬性的取值「高」、「中」、「低」，可轉化為({1.0, 0.5, 0.0})。

若不存在序關係，則假定有 (k) 種可能的屬性值，將其轉化為 (k) 維向量。

如「瓜類」屬性的取值有「冬瓜」、「西瓜」、「南瓜」，可轉化為 ((0,0,1),(0,1,0),(1,0,0))。

線性回歸試圖學得：

為使 (f(x_i)simeq y_i)，即：使 (f(x)) 與 (y) 之間的差別最小化。
考慮回歸問題的常用性能度量——均方誤差（亦稱平方損失（square loss）），即讓均方誤差最小化：

(w^*,b^*) 表示 (w) 和 (b) 的解。
均方誤差對應了歐幾里得距離，簡稱歐氏距離（Euclidean distance）。
基於均方誤差最小化來進行模型求解的方法稱為最小二乘法（least square method）。在線性回歸中，就是試圖找到一條直線，使得所有樣本到直線上的歐氏距離之和最小。

下面需要求解 (w) 和 (b) 使得 (E_{(w,b)} = sumlimits_{i=1}^m(y_i-wx_i-b)^2) 最小化，該求解過程稱為線性回歸模型的最小二乘參數估計（parameter estimation）。

(E_{(w,b)}) 為關於 (w) 和 (b) 的凸函數，當它關於 (w) 和 (b) 的導數均為 (0) 時，得到 (w) 和 (b) 的最優解。將 (E_{(w,b)}) 分別對 (w) 和 (b) 求導數得：

令式子 (1.6) 和 (1.7) 為 (0) 得到 (w) 和 (b) 的最優解的閉式（closed-form）解：

其中 (overline{x} = frac{1}{m}sumlimits_{i=1}^m x_i) 為 (x) 的均值。

3. 一元線性回歸的Python實現

現有如下訓練數據，我們希望通過分析披薩的直徑與價格的線性關係，來預測任一直徑的披薩的價格。

其中 Diameter 為披薩直徑，單位為「英寸」；Price 為披薩價格，單位為「美元」。

3.1 使用 stikit-learn

3.1.1 導入必要模組

import matplotlib.pyplot as plt  import numpy as np  import pandas as pd  from sklearn.linear_model import LinearRegression  

3.1.2 使用 Pandas 載入數據

pizza = pd.read_csv("pizza.csv", index_col='Id')  pizza.head()  # 查看數據集的前5行  

3.1.3 快速查看數據

我們可以使用 matplotlib 畫出數據的散點圖，x 軸表示披薩直徑，y 軸表示披薩價格。

def runplt():      plt.figure()      plt.title("Pizza price plotted against diameter")      plt.xlabel('Diameter')      plt.ylabel('Price')      plt.grid(True)      plt.xlim(0, 25)      plt.ylim(0, 25)      return plt    dia = pizza.loc[:,'Diameter'].values  price = pizza.loc[:,'Price'].values  print(dia)  print(price)  plt = runplt()  plt.plot(dia, price, 'k.')  plt.show()  

[ 6  8 10 14 18]  [ 7.   9.  13.  17.5 18. ]  

3.1.4 使用 stlearn 創建模型

model = LinearRegression()  # 創建模型  X = dia.reshape((-1,1))  y = price  model.fit(X, y)  # 擬合    X2 = [[0], [25]] # 取兩個預測值  y2 = model.predict(X2)  # 進行預測  print(y2)  # 查看預測值    plt = runplt()  plt.plot(dia, price, 'k.')  plt.plot(X2, y2, 'g-')  # 畫出擬合曲線  plt.show()  

[ 1.96551724 26.37284483]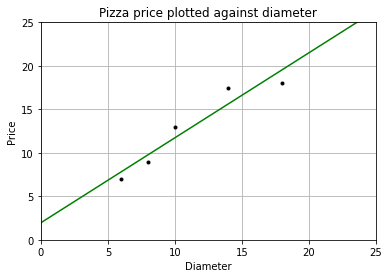  

這裡 fit()方法學得了一元線性回歸模型 (f(x) = wx+b)，這裡 (x) 指披薩的直徑，(f(x)) 為預測的披薩的價格。

fit() 的第一個參數 X 為 shape(樣本個數，屬性個數) 的數組或矩陣類型的參數，代表輸入空間；
第二個參數 y 為 shape(樣本個數,) 的數組類型的參數，代表輸出空間。

3.1.5 模型評估

成本函數（cost function）也叫損失函數（lost function），用來定義模型與觀測值的誤差。

模型預測的價格和訓練集數據的差異稱為訓練誤差（training error）也稱殘差（residuals）。

plt = runplt()  plt.plot(dia, price, 'k.')  plt.plot(X2, y2, 'g-')    # 畫出殘差  yr = model.predict(X)  for index, x in enumerate(X):      plt.plot([x, x], [y[index], yr[index]], 'r-')    plt.show()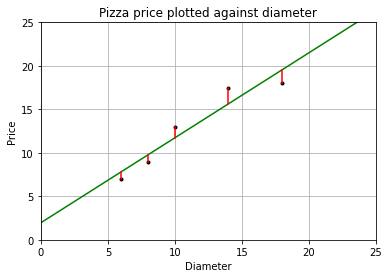  

根據最小二乘法，要得到更高的性能，就是讓均方誤差最小化，而均方誤差就是殘差平方和的平均值。

print("均方誤差為: %.2f" % np.mean((model.predict(X)-y) ** 2))  

均方誤差為: 1.75  

3.2 手動實現

3.2.1 計算 w 和 b

(w) 和 (b) 的最優解的閉式（closed-form）解為：

其中 (overline{x} = frac{1}{m}sumlimits_{i=1}^m x_i) 為 (x) 的均值。

下面使用 Python 計算 (w) 和 (b) 的值：

w = np.sum(price * (dia - np.mean(dia))) / (np.sum(dia**2) - (1/dia.size) * (np.sum(dia))**2)  b = (1 / dia.size) * np.sum(price - w * dia)  print("w = %fnb = %f" % (w, b))    y_pred = w * dia + b    plt = runplt()  plt.plot(dia, price, 'k.')  # 樣本點  plt.plot(dia, y_pred, 'b-')  # 手動求出的線性回歸模型  plt.plot(X2, y2, 'g-.')  # 使用LinearRegression.fit()求出的模型  plt.show()  

w = 0.976293  b = 1.965517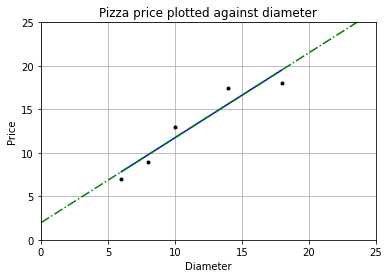  

可以看到兩條直線重合，我們求出的回歸模型與使用庫求出的回歸模型相同。

3.2.2 功能封裝

將上述程式碼封裝成類：

class LinearRegression:      """      擬合一元線性回歸模型        Parameters      ----------      x : shape 為(樣本個數,)的 numpy.array          只有一個屬性的數據集        y : shape 為(樣本個數,)的 numpy.array          標記空間        Returns      -------      self : 返回 self 的實例.      """      def __init__(self):          self.w = None          self.b = None        def fit(self, x, y):          self.w = np.sum(y * (x - np.mean(x))) / (np.sum(x**2) - (1/x.size) * (np.sum(x))**2)          self.b = (1 / x.size) * np.sum(y - self.w * x)          return self        def predict(self, x):          """          使用該線性模型進行預測            Parameters          ----------          x : 數值 或 shape 為(樣本個數,)的 numpy.array              屬性值            Returns          -------          C : 返回預測值          """          return self.w * x + self.b  

使用：

# 創建並擬合模型  model = LinearRegression()  model.fit(dia, price)    x2 = np.array([0, 25])  # 取兩個預測值  y2 = model.predict(x2)  # 進行預測  print(y2)  # 查看預測值    runplt()  plt.plot(dia, price, 'b.')  plt.plot(x2, y2, 'y-')  # 畫出擬合  plt.show()  

[ 1.96551724 26.37284483]  

此文原創禁止轉載，轉載文章請聯繫部落客並註明來源和出處，謝謝！
作者: Raina_RLN https://www.cnblogs.com/raina/