數據挖掘之異常檢測(一)
- 2020 年 3 月 29 日
- 筆記
看了數據挖掘的異常檢測部分,寫一點筆記。
1.0 概述
什麼是數據挖掘:數據挖掘
什麼是異常檢測:異常檢測
異常檢測的目標是發現與大部分其他對象不同的對象。通常,異常對象被稱為離群點,因為在數據的散布圖中,他們遠離其他數據點。異常檢測也稱為偏差檢測、例外挖掘。
異常檢測的方法各種各樣,所有這些的思想都是:異常的數據對象是不尋常的,或者在某些方面與其他對象不一致。
1.1 異常的成因
- 數據來源於不同的類
- 自然變異
- 數據測量和收集誤差
1.2 異常檢測方法
1. 基於模型的技術
首先建立一個模型,異常是那些不能完美匹配的對象。例如,數據分布模型可以通過估計概率分布的參數來創建。如果一個對象不能很好地同該模型擬合,即如果它很可能不服從該分布,則它是一個異常。
2. 基於近鄰度的技術
可以在對象之間定義鄰近性度量,許多異常檢測方法都基於鄰近度。異常對象是那些遠離大部分其他對象的對象。當數據用二維或三維散布圖顯示,可以從視覺上檢測出基於距離的離群點。
3. 基於密度的技術
對象的密度估計可以相對直接地計算,特別是當對象之間存在近鄰性度量時,低密度區域中的對象相對遠離近鄰,可能被看做異常。
1.3 類標號的使用
異常檢測的三種基本方法:
- 非監督的
- 監督的
- 半監督的
三者的主要區別至少對於對於某些數據而言是類標號(異常或正常)可以利用的程度。
1. 監督的異常檢測
要求存在異常類和正常類的訓練集(注意:可能有多個正常類或者異常類)
2. 非監督的異常檢測
沒有提供類標號。在這種情況下,目標是將一個得分(或標號)賦予每個實例,反映該實例是異常的程度。注意,許多相似的異常可能會導致被標記為正常,或有較低的離群點得分。
3. 半監督的異常檢測
訓練數據包含被標記的正常數據,但是沒有關於異常對象的資訊。目標是使用有標記的正常對象的資訊,對於給定的對象集合,發現異常標號。
1.4 問題
1. 用於定義異常的屬性個數
對象可以有許多屬性,它可能在某些屬性上具有異常值,而在其他屬性上具有正常值。注意,即使一個對象的所有屬性值都不是異常,對象也可能異常。
2. 點的異常程度
二元方式報告對象是否異常:要麼正常要麼不正常。這不能反映某些對象比其他對象更加極端異常的基本事實。需要有某種對象異常程度的評估,這種評估稱為異常或離群點得分。
3. 全局觀點與局部觀點
一個對象可能相對於所有對象看上去不正常,但是相對於它的局部近鄰並非如此。
4. 一次識別一個與多個異常
一次一個:每次識別並刪除最異常的實例,重複該過程。一次多個:異常集族一起識別。前者常遇到屏蔽問題,後者可能陷入泥潭。
5. 評估
6. 有效性
各種方案的計算開銷顯著不同。
2.0 統計方法
統計學方法是基於模型的方法,即為數據創建模型,根據對象的擬合程度來評估他們。
定義 離群點:離群點是一個對象,關於數據的概率分布模型,它具有低概率。
問題:
1. 識別數據集的具體分布
2. 使用屬性的個數
3. 混合分布
2.1 檢測一元正態分布的離群點
高斯分布 N(μ,σ),第一個參數為均值,第二個為標準差。下圖為均值為0,標準差為1的高斯分布的概率密度函數:
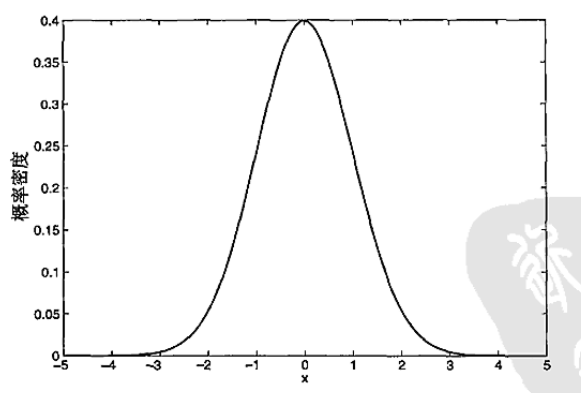
來自N(0,1)分布的對象,出現在尾部的機會很小
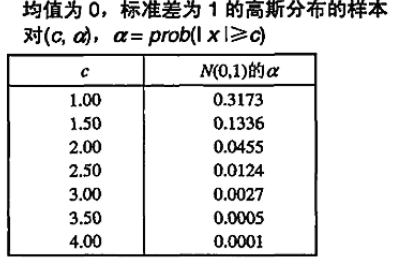
因為值到N(0,1)分布中心的距離 c 直接與該值的概率相關,因此可以使用它作為檢測對象(值)是否是離群點的基礎。
2.2 多元正態分布的離群點
由於不同變數(屬性)之間的相關性,多元正態分布並不關於它的中心對稱,如下圖,該分布均值為(0,0),協方差矩陣為
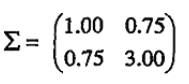
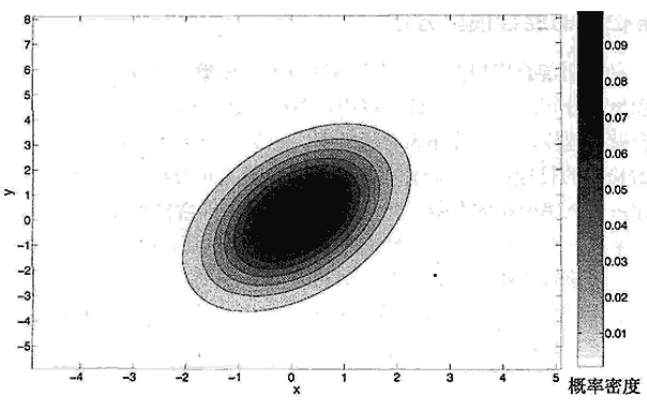
什麼是協方差矩陣: 協方差矩陣
如果我們打算用一個簡單的閥值來決定一個對象是否是離群點,可以用 Mahalanobis 距離,它是是一種考慮數據分布形狀的距離度量。
2.3 異常檢測的混合模型方法
數據用兩個分布的混合模型建模,一個分布為普通數據;另一個為離群點。
初始時將所有對象放入普通對象集,而異常對象集為空。然後用一個迭代過程將對象從普通集轉移到異常集,只要該轉移能提高數據的總似然(數據和模型之間的相似度)。
假定數據集D包含來自兩個概率分布的對象:M是大多數(正常)對象的分布,A是異常對象的分布,則數據的總概率分布可以記作:D(x) = (1 – λ) + λA(x)
其中,x是一個對象,λ是一個0 – 1之間的數,給出離群點的期望比例。M由數據估計,A通常取均勻分布。初始時刻 t = 0,M0 = D,A0為空。在任意時刻 t,整個數據集的似然和對數似然分別為以下兩式:
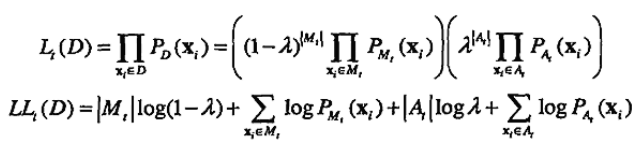
PD、PMt 和 PAt 分別是 D、Mt 和 At 的概率分布函數。
因為正常對象的數量比異常對象大得多,因此當一個對象移動到異常集後,正常的分布變化不大。這時,每個正常對象對正常對象的總似然的貢獻保持相對不變。
另外,如果假定異常服從均勻分布,則移動到異常集的每個對象對異常的似然貢獻一個固定的量。這樣,當一個對象移動到異常集時,數據總似然的改變粗略等於該對象在均勻分布下的概率(用λ加權)減去該對象在正常數據點的分布下的概率(用1-λ加權)。從而,異常集由這樣一些對象組成,這些對象在均勻分布下的概率明顯比在正常對象分布下的概率高。

