Slam筆記I
- 2020 年 3 月 29 日
- 筆記
視覺Slam筆記I
第二講-三位空間剛體運動
點與坐標系：
基礎概念：
-
坐標系：左手系和右手系。右手系更常用。定義坐標系時，會定義世界坐標系，相機坐標系，以及其他關心對象的坐標系。空間中任意一點可由空間的基的線性表出。
-
加減法：用坐標描述更方便。
-
內積：點乘得數，即
-
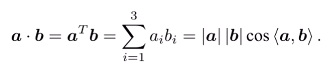
外積：叉乘得向量，即
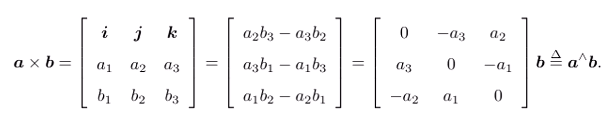右手系下，得到按照右手定則獲取的向量。 -
坐標系間的變換：
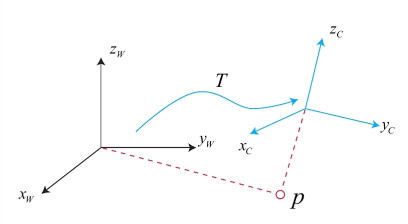
通過平移(向量的加減)和旋轉(有多種描述方式，見下) -
2D情況：二維坐標點表示位置+一個旋轉角表示朝向。
-
3D情況：三維坐標點表示位置+一個旋轉角(角度間的變換使用旋轉，旋轉方式有多種，見下)。
旋轉矩陣：（描述旋轉的第一種方式）
坐標系 (e_1,e_2,e_3)經過旋轉變成 (e'_1,e'_2,e'_3)，在三維空間中，向量 a保持不動，那麼如何表出它在 (e'_1,e'_2,e'_3)下的坐標：
- 線性表出法向量
a坐標：兩坐標系實質是分別用兩組不同的基去表示同一個點，則兩者的線性組合是相等的：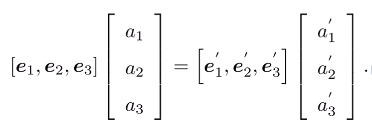
- 左右兩邊同時左乘
(e_1,e_2,e_3)的轉置，得到：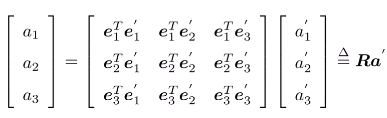
- R即為旋轉矩陣。
- 性質：
- R是一個正交矩陣（矩陣的逆即矩陣的轉置，或轉置×本身即為一個單位矩陣）。
- R的行列式值為1。
- 滿足上述性質的矩陣都可以稱為旋轉矩陣，使用集合表示：
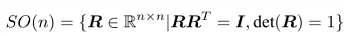
，又稱特殊正交群SO(3)。 - 固定表示方式（下標順序）：
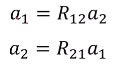且滿足矩陣關係：
。
因此，空間中不同坐標系下點坐標的變換可以使用：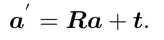
即旋轉+平移的形式完全描述
- 理論依據：歐拉定理，剛體在三維空間中的一般運動，可分解為剛體上方某一點的平移，以及繞經過此點的旋轉軸的轉動。
但是，這種表示方式在多次進行變換時會有不便（
），因此使用增廣的方式進行表示：
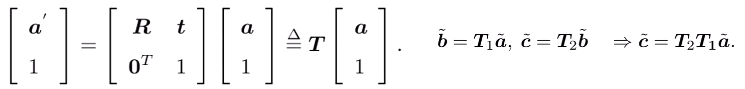
- 其中，
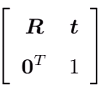稱為變換矩陣，
的形式稱為齊次坐標。 - 齊次坐標性質：齊次坐標乘上任意非0常數時仍表達同一坐標
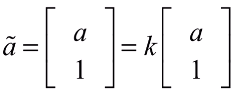
- 變換矩陣的集合：稱為特殊歐式群SE(3)：
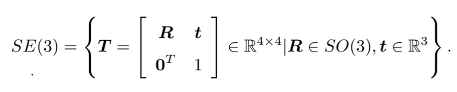
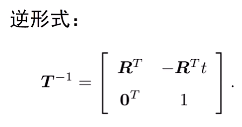
旋轉向量和歐拉角：
旋轉矩陣在實際中更常用，但這些概念也是需要清楚的。
旋轉矩陣R是一個3×3的矩陣，有九個元素，但僅有三個自由度，也就是存在描述方式上的冗餘，那麼能否以更少的元素表達旋轉？
剛體旋轉存在一個轉軸(向量)，還有轉過的角度，於是想用角度乘以向量(單位化過後)的形式去描述旋轉。
旋轉向量
-
一個向量，方向為旋轉軸方向，長度為轉過的角度。(單位向量乘角度大小)
-
又稱角軸/軸角。
-
羅德里格斯公式可以將旋轉向量(n,theta)轉換成旋轉矩陣R：
-
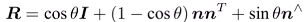
旋轉矩陣R也可以轉換成旋轉向量(n,theta)：
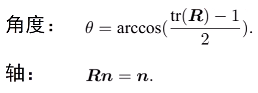n是特徵向量。
歐拉角
- 將旋轉分解成三個方向上的轉動，常用順序為yaw-pitch-roll(也就是繞Z-Y-X方式轉，注意 ，不同地方在繞Z轉之後，所繞的Y軸可能是原來的Y軸，也可能是轉動後的Y軸)
- 萬向鎖(Gimbal Lock)：歐拉角存在奇異性(特定值下，旋轉的自由度減1)
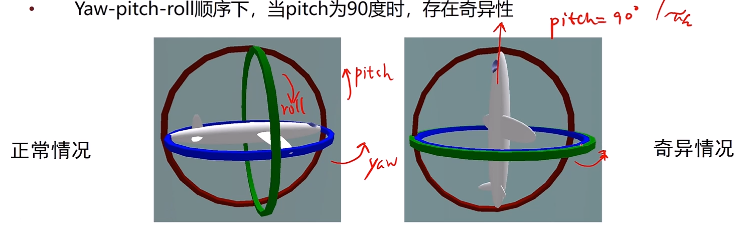在pitch方向旋轉完畢後，roll方向旋轉和yaw方向旋轉是重合的。由此，歐拉角不適合插值或迭代，故不常用。
四元數：
吸取了旋轉矩陣和旋轉向量、歐拉角的優點，是一種優秀的描述方式。
- 2D情況下，可以用單位複數表達旋轉：
- 用z乘以i，相當於旋轉了90度(
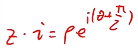)，乘-i轉動-90度。
在三維情況下，四元數可作為擴充定義的複數
-
特點1：有三個虛部+一個實部
-
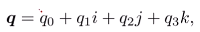
特點2：虛部之間存在關係：
-
單位四元數可以表達三維空間的旋轉：
-
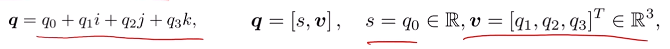
四元數也能定義很多運算：
-
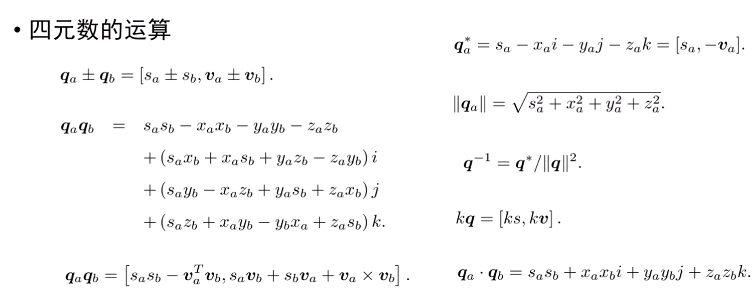
四元數轉換成旋轉向量：
-
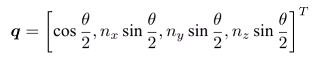
旋轉向量轉換成四元數：
-
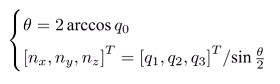
用四元數表示旋轉：
