tarjan演算法強連通分量的正確性解釋+錯誤更新方法的解釋!!!+hdu1269
- 2020 年 3 月 28 日
- 筆記
題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=1269
以下內容為原創,轉載請聲明。
強連通分量SCC(Strongly Connected Component):一個圖的子圖,如果任何兩個點都互相可達且滿足最大性,該子圖就是原圖的SCC。
對於有向圖的連通性,tarjan可以說是十分牛逼了,由於tarjan只需要一次dfs就能判斷有向圖中所有的SCC,所以他的複雜度是O(|V|+|E|),也就是把每條邊和每個點都會檢索一遍,是在線性時間能處理出所有的SCC的!下面簡單說明求強連通分量的tarjan演算法的過程以及正確性。
基礎知識:
①、經dfs處理過的點的low值相同的一定屬於同一個SCC,這個SCC中第一個被dfs訪問的點也就是dfn=low的點一定就是這個SCC中每個點的low值,顯而易見。
②、在dfs過程中,dfs進行最深處一定會進入某一個SCC,(儘管在過程中可能會進入其他SCC),下面我會解釋
③、標記SCC Number的過程可以用棧實現,因為dfs的過程就是遞歸,遞歸和棧非常相似
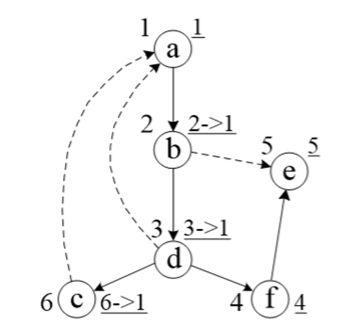
tarjan演算法的流程:將每個訪問的點入棧,更新low值,直到到達一個點,這個點low值等於dfn值,說明這個點一定是一個SCC的祖先,也就是第一個訪問的點,此時這個點一定在棧的底部!!因為是通過dfs退出多次而不彈棧才得到這個low=dfn。我們只要不斷彈出l這個SCC的點並標記就可以,直到彈到棧底。我們先看基礎知識(2),上圖中在訪問3的時候進入了4、5結點,也就是其他SCC,到了5的時候,由於low[5]=dfn[5]所以此時彈棧,發現就只有一個5屬於這個SCC,4也是同樣的過程,直到到了3,進入另一個分支6,這就是我基礎知識(2)中的一定會在最終進入一個SCC而且棧底元素就是這個SCC的祖結點。
關於強連通分量處理回退邊的方式,我的解釋是這樣的:
當一個點已經標記過dfn之後,而且這個點在之前沒有標記過SCC(因為在dfs過程中會進入並處理其他SCC,若此時有邊相連就無需更新,因為回退邊所到點的low值一定小於該點的low)就用
①、low[u]=min(low[v],dfn[v]) ②、low[u]=min(low[v],low[u])
來更新low值,其實對於雙連通分量來說,這兩種更新方式的結果是一樣的,但是第一種方法在原理上是錯誤的!!!!! 我來舉一個例子,又是下面這張圖,
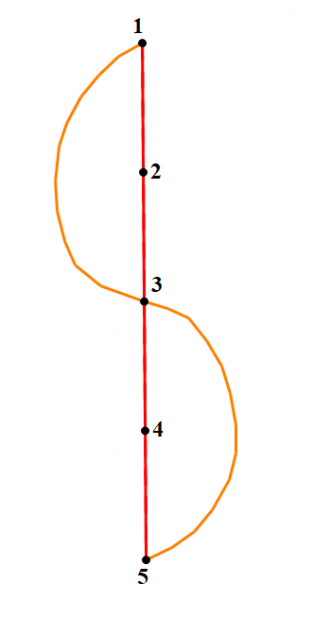
對於第一種我們得出的結果是下面第一張圖,而對於第二張我們得到的結果是下面第二張圖,我們可以發現,根據tarjan演算法的思想,處於同一個強連通分量中的點low值應該是相同的,但是第一種做法中的點的low值是不同的,但是他們得到的結果都是一樣的,都是圖是強連通的,為什麼呢?

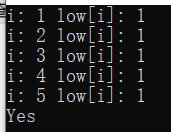
下面我將證明第一種做法得出正確結果的原因:
由於對於4,5號節點來說,他們的low值為3的時候,都與他們的dfn值不相同(dfn[4]=4&dfn[5]=5),所以他們就會一直在棧中,而棧底也一定是1號結點。4,5號結點沒有機會彈出,直到dfs return到1號結點,此時才會彈棧,一直到彈出1號結點為止,這就把棧中的結點4,5彈出了,但是事實上他們的low值是更新錯誤的。儘管是錯誤的,但是中途dfs在訪問其他SCC的時候(如果有的話,可以參考最上面那張圖)已經把其他SCC的點都標記了,此時棧中剩下的只有這一個SCC!!所以最終的結果是相同的,但是!!這種更新方法是錯誤的!!因為在之後不能通過他們的不同的low值數量去查看SCC的數量,只能從每一次彈棧中給出的SCCNUMBER中得到SCC的資訊。而且,這種做法跟tarjan的演算法中“每個SCC”的low值是相同的是矛盾的。
看完我的文章能不能支援一下呢
hdu1269程式碼如下:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef unsigned int ui; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 #define pf printf 7 #define mem(a,b) memset(a,b,sizeof(a)) 8 #define prime1 1e9+7 9 #define prime2 1e9+9 10 #define pi 3.14159265 11 #define lson l,mid,rt<<1 12 #define rson mid+1,r,rt<<1|1 13 #define scand(x) scanf("%llf",&x) 14 #define f(i,a,b) for(int i=a;i<=b;i++) 15 #define scan(a) scanf("%d",&a) 16 #define mp(a,b) make_pair((a),(b)) 17 #define P pair<int,int> 18 #define dbg(args) cout<<#args<<":"<<args<<endl; 19 #define inf 0x3f3f3f3f 20 inline int read(){ 21 int ans=0,w=1; 22 char ch=getchar(); 23 while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();} 24 while(isdigit(ch))ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); 25 return ans*w; 26 } 27 const int maxn=1e5+10; 28 int n,m,t; 29 int head[maxn],nxt[maxn],low[maxn],sccno[maxn],dfn[maxn],id; 30 struct node{ 31 int u,v; 32 }p[maxn*10]; 33 int e=0; 34 int cnt; 35 stack<int> sk; 36 void addedge(int u,int v) 37 { 38 p[e].u=u; 39 p[e].v=v; 40 nxt[e]=head[u]; 41 head[u]=e++; 42 } 43 void tarjan(int u) 44 { 45 low[u]=dfn[u]=++id; 46 sk.push(u);//將結點編號壓棧 47 for(int i=head[u];~i;i=nxt[i]) 48 { 49 int v=p[i].v; 50 if(!dfn[v]) 51 { 52 tarjan(v); 53 low[u]=min(low[u],low[v]); 54 } 55 else if(!sccno[v])//回退邊且邊終點沒有標記SCC 56 low[u]=min(low[u],low[v]); 57 } 58 if(low[u]==dfn[u]) 59 { 60 cnt++;//連通分量的數量增加,對每個點這個if語句只執行一次 61 while(1) 62 { 63 int v=sk.top(); 64 sk.pop(); 65 sccno[v]=cnt; 66 if(u==v)break; 67 } 68 } 69 } 70 int main() 71 { 72 freopen("input.txt","r",stdin); 73 //freopen("output.txt","w",stdout); 74 std::ios::sync_with_stdio(false); 75 while(scanf("%d%d",&n,&m)==2) 76 { 77 if(n==0&&m==0)break; 78 e=0;cnt=0; 79 mem(head,-1);mem(nxt,-1); 80 while(!sk.empty())sk.pop(); 81 int x,y; 82 f(i,1,m) 83 { 84 x=read(); 85 y=read(); 86 addedge(x,y); 87 } 88 mem(dfn,0); 89 id=0; 90 mem(sccno,0); 91 mem(low,0); 92 f(i,1,n) 93 { 94 if(!dfn[i]) 95 tarjan(i); 96 } 97 f(i,1,n)dbg(low[i]); 98 if(cnt==1)pf("Yesn"); 99 else pf("Non"); 100 } 101 }