K:劍指offer-56 題解 誰說數字電路的知識不能用到演算法中?從次數統計到邏輯表達式的推導,一文包你全懂
- 2020 年 3 月 28 日
- 筆記
前言:
本題解整理了一位大佬在leetcode中的程式碼的方法,該博文致力於讓所有人都能夠能夠看懂該方法。為此,本題解將從統計數字出現次數的解題方式開始講起,再推導出逐位統計的解題方式,期望以循序漸進的方式得出最終程式碼的思想。
相關知識關鍵字:
二進位、位運算、真值表、邏輯表達式、狀態機
題目:
劍指offer 56 II. 數組中數字出現的次數 II
在一個數組 nums 中除一個數字只出現一次之外,其他數字都出現了三次。請找出那個只出現一次的數字。
示例 1:
輸入:nums = [3,4,3,3]
輸出:4
示例 2:
輸入:nums = [9,1,7,9,7,9,7]
輸出:1
題解:
對於數組nums,其只有一個數字出現了一次,其餘數字均出現了三次,一種直觀的想法是直接採用一個map統計各個字元出現的次數,最後再遍歷map中的各個鍵值對,直到找到只出現了一次的數字。其程式碼如下
public int singleNumber(int[] nums) { //統計各個數字出現的次數,鍵為數字,值為出現的次數 Map<Integer,Integer> map =new HashMap<Integer,Integer>(); for(int i:nums){ if(!map.containsKey(i)){ map.put(i,1); continue; } map.put(i,map.get(i)+1); } //遍歷map中的鍵值對,查看值出現次數為1的鍵,即為答案 int result = 0; for(Map.Entry<Integer,Integer> entry:map.entrySet()){ if(entry.getValue()==1){ result = entry.getKey(); break; } } return result; } 對於該解題方法,其空間複雜度為O(n),時間複雜度為O(n),這顯然不會是該題的最優解。
在得出逐位運算的解題方式之前,我們需要研究下該數組中的數字用二進位的方式進行表示的特點。
以題干給出的示例1為例,nums=[3,4,3,3],將數組中各個數字採用二進位的方式寫出,
3 = (0011)2
4 = (0100)2
3 = (0011)2
3 = (0011)2
通過對數組中各個數的二進位表示形式逐位進行觀察,我們可以發現,當數組中只出現一次的那個數字(用k表示)在二進位的對應位為0時,該對應位為1在數組各個數字中出現的總次數應當為3^n ,當k的對應位為1時,該對應位為1在數組各個數字中出現的總次數應當為 3^n + 1,為此,我們可以統計數字中的各個位中1出現的次數,當為3^n 次時,只出現一次的數字的對應位應當為0,當為3^n + 1次時,只出現一次的數字的對應位應當為1。由此,我們可以得到如下程式碼:
public int singleNumber(int[] nums) { if(nums==null||nums.length==0) return 0; int result = 0; for(int i = 0;i<32;i++){ //統計該位1的出現次數情況 int count = 0; int index = 1<<i; for(int j:nums){ //該位與操作後的結果不為0,則表示該位為1的情況出現了 if((index&j)!=0){ count++; } } //該位上出現1的次數mod3後為1,表示出現一次的數字該位為1 if(count%3==1){ result|=index; } } return result; } 對於該解題方法,其時間複雜度為O(n),空間複雜度為O(1)。在某種程度上,這是最優解了。但是,該題解仍有改進的空間(其時間複雜度的常係數為32)。
有了對數組中數字的各二進位位進行逐一統計分析出現次數的相關基礎後,我們便可以推導出那個擊敗100%的答案的解法了。回顧上面的解題方法的分析部分,其需要我們對數字的二進位位逐位進行統計,對於int數據類型,我們需要遍歷32次數組(int佔4位元組),以便統計出各個二進位位出現的次數。那我們有沒有辦法只遍歷一次數組便得出答案呢?當然有,我們可以一次分析32bit的int的各個位在數組的各個數字中出現的次數。在分析上面的程式碼我們可以發現,實際上,我們只需要記錄對應位出現的次數為0、1、2次的情況,當對應位出現次數為3的時候,我們便可以將該位出現的次數置為0,重新開始進行計數。由於int型中的各個二進位位出現的次數為3進位的,為此我們需要兩個位來記錄各個位出現的次數,由此我們需要引入兩個變數a,b來統計對應位出現的次數。由ab兩個變數組合起來來記錄各個二進位位出現為1的情況。變數a表示高位的情況,變數b表示低位的情況,而在遍曆數組運算完成之後,遍歷b的值便是答案。
變數ab組合的各個二進位位組合的形式有如下三種,考慮進新引入的變數c的各二進位位的情況,我們可以得到如下真值表:
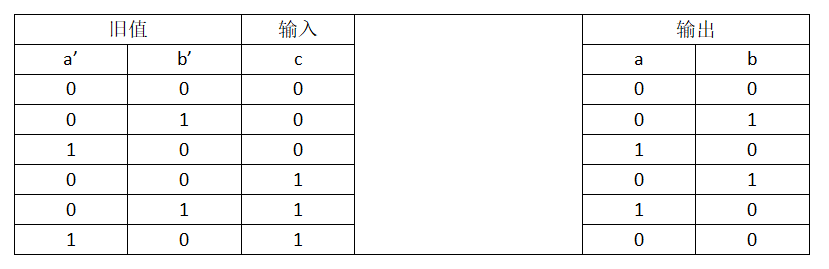
由以上真值表,我們便可得出變數a,b的邏輯表達式,其表示如下
a = a』(!b』)(!c)+(!a』)b』c
b = (!a』)b』(!c)+(!a』)(!b』)c = (!a』)[b』(!c)+(!b』)c] = (!a』)[b』^c]
由此,我們可以得到如下程式碼
public int singleNumber(int[] nums) { //a對應位為1表示出現2次的記錄,b對應位表示出現1次或0次的記錄,ab共同組成該位出現的次數 int a = 0,b =0; for(int i:nums){ int temp = a; a = (~a&b&i)|(a&~b&~i); b = ~temp&(b^i); } return b; } 實際上,我們還能對a的邏輯表達式進行簡化,先得到b的邏輯表達式,之後用b代替b』作為輸入,由此可以簡化a為
a = (!a』)(!b)c+a』(!b)(!c) = (!b)[(!a』)c+a』(!c)] = (!b)[a』^c]
由此,我們可以得到如下程式碼
public int singleNumber(int[] nums) { //a為對應位的1出現2次的記錄,b為對應位出現1次的記錄,ab共同組成該位出現的次數 int a = 0,b =0; for(int i:nums){ b = ~a&(b^i); a = ~b&(a^i); } return b; } 至此,我們得到了最終的程式碼。
這個是本人的公眾號,致力於寫出絕大部分人都能讀懂的技術文章。歡迎相互交流,我們博採眾長,共同進步。


