【面試QA-基本模型】RNN 與 CNN

  • 2020 年 3 月 27 日
  • 筆記

目錄

為什麼傳統 CNN 適用於 CV 任務，RNN 適用於 NLP 任務

從模型特點上來說：

  • 對於 CNN 每一個卷積核都可以看作是一個濾波器，卷積運算的本質是互相關運算，每個卷積核僅對於具有特定特徵具有較大的激活值，而且 CNN 有參數共享和局部連接的特點，能夠提取影像上不同位置的同一個特徵，即 CNN 具有平移不變性

  • RNN 的特點在於其是一個時序模型，在對每個神經元不僅可以接收當前時刻的輸入資訊，還將接收上一個時刻的該神經元的輸出資訊，具有短期記憶能力。這在用於 NLP 任務時相當於隱含著建立了一個語言模型，這對詞序具有很強的區分能力。而 CNN 和 DNN 均類似詞袋模型，丟失的詞序特徵。

從數據特徵上來說

  • 影像矩陣中的每個元素為影像中的像素值，每個像素與其周圍元素都是高度相關的
  • 文本矩陣中的數據為詞的 embedding 向量，每個元素在詞向量內與詞向量間的相鄰元素的關聯性是不同的，因此 CNN 用於 NLP 任務常使用的是一維卷積

CNN 與 FCN 相比有什麼優點？

  • CNN 相比於 FCN 具有更少的參數，主要有下面兩個原因：
    • 參數共享：一個卷積核能對樣本影像上的所有區域採用相同的參數進行特徵檢測。
    • 稀疏連接：在每一層中，由於濾波器的尺寸限制，輸入和輸出之間的連接是稀疏的，每個輸出值只取決於輸入在局部的一小部分值。
  • 池化層降維：池化過程則在卷積後很好地聚合了特徵，通過降維來減少運算量。
  • 由於 CNN 參數數量較小，所需的訓練樣本就相對較少，因此在一定程度上不容易發生過擬合現象。
  • 平移不變性：CNN 比較擅長捕捉區域位置偏移。即進行物體檢測時，不太受物體在圖片中位置的影響，增加檢測的準確性和系統的健壯性。

CNN的相關計算

  • 輸出維度計算

    • 輸出維度 = (輸入維度 – 卷積核大小 + 2*Padding長度)/步長 + 1

  • 感受野的計算

    • 第k-1層的感受野 = (第k層的感受野 – 1) * 步長 + 卷積核大小

  • 卷積核的參數量

    • 參數量=（filter size * 輸入通道數 ）* 當前層 filter 數量

  • 卷積核的計算量

    • 計算量 = 輸出的維度^2 * 輸出的通道數 * 卷積核個數 * 卷積核大小^2

RNN 原理

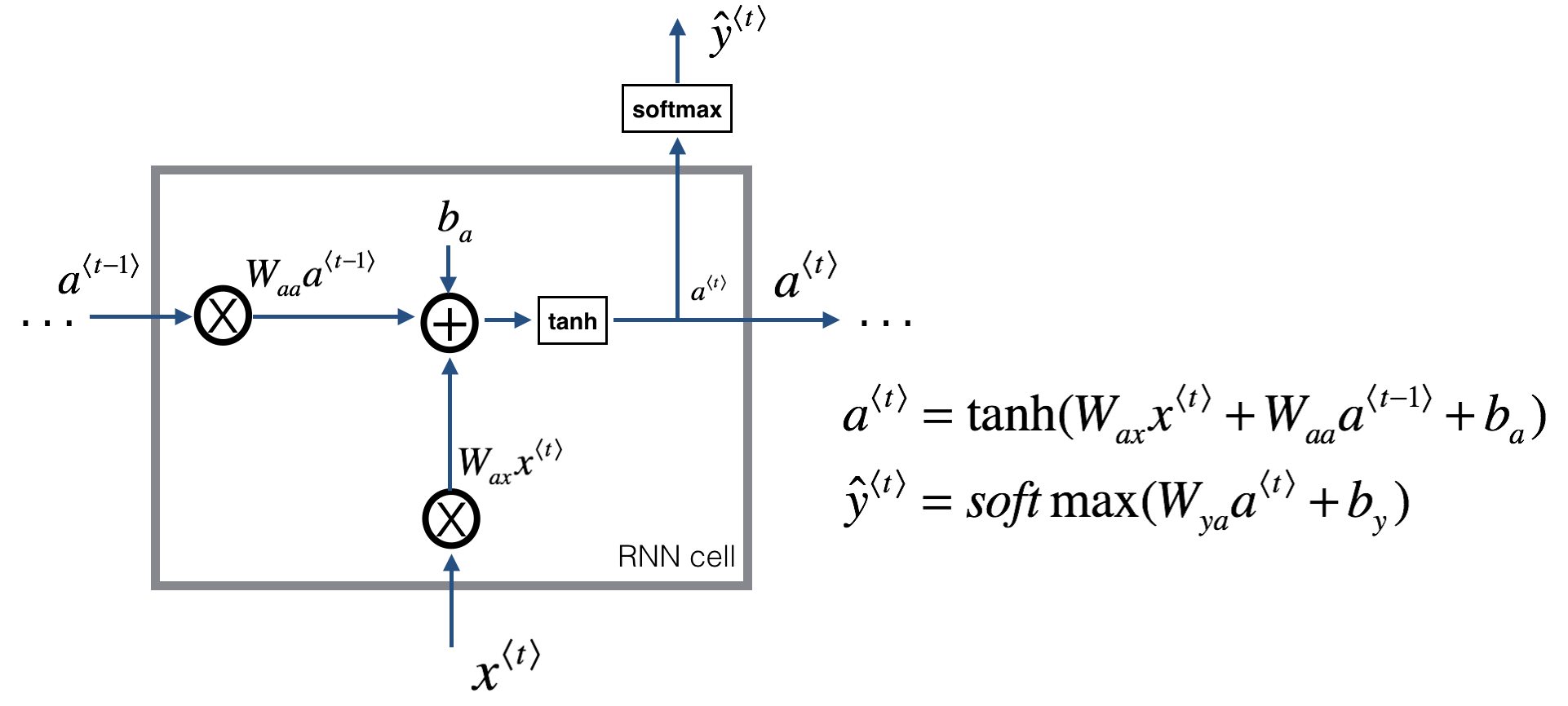
(hat y) 部分的激活函數可以根據下游任務設置

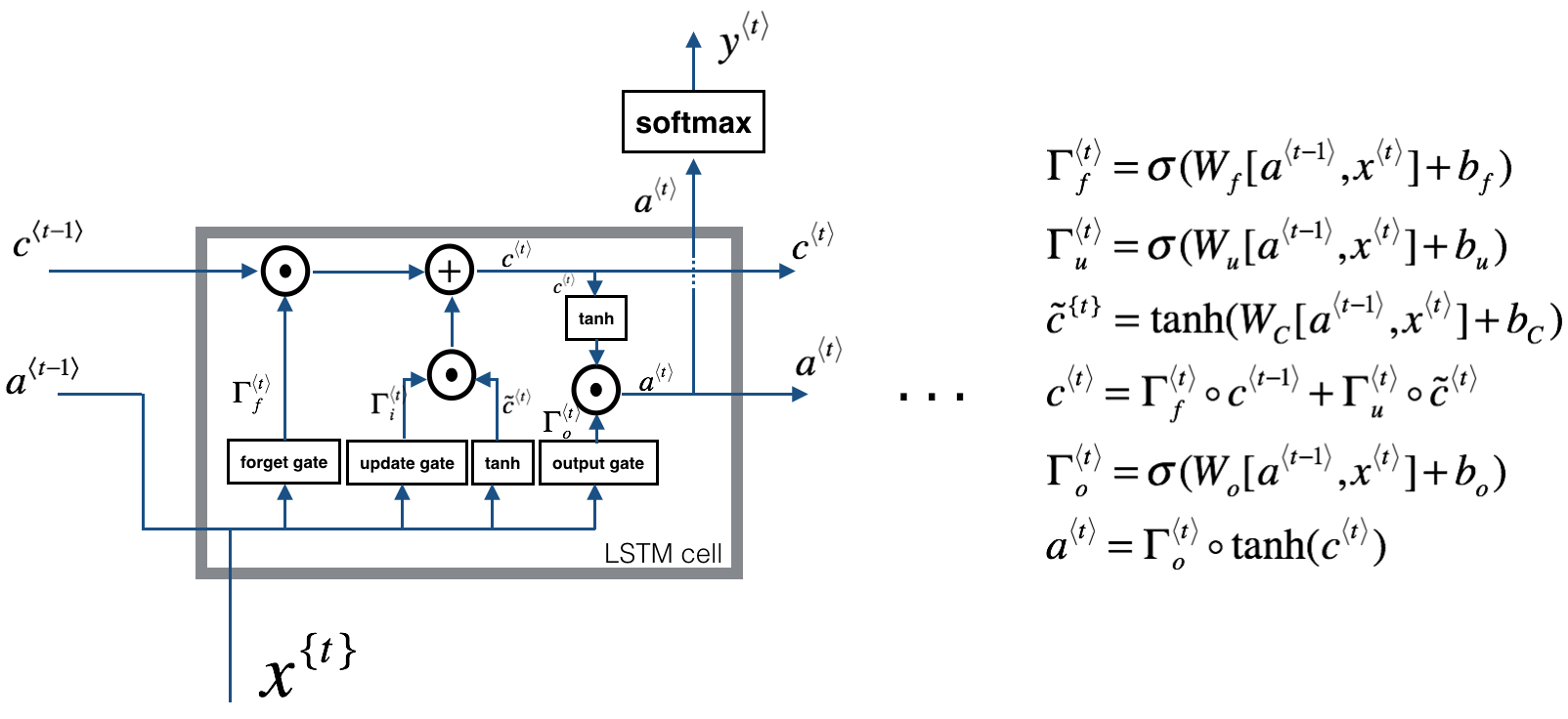
LSTM 原理

  • 三個門：[output_dim + input_dim, 1]
  • 更新門位置的全連接層：[output_dim + input_dim, output_dim]

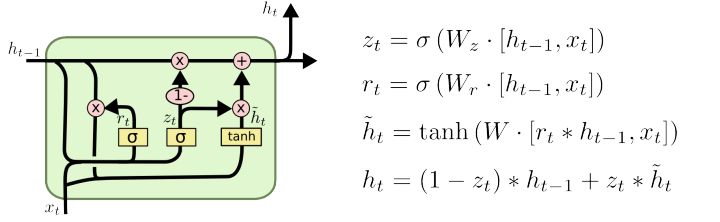
GRU 原理

  • 兩個門：[output_dim + input_dim, 1]
  • 全連接層：[output_dim + input_dim, output_dim]

RNN BPTT

– 假設$t$時刻的損失函數為$L_t$，以 $W_{aa}$，$W_{ax}$，$W_{ya}$ 為例 $$ begin{aligned} &frac{delta L_t}{delta W_{ya}} = frac{delta L_3}{delta hat{y}_t}frac{delta hat{y}_t}{delta W_{ya}} \ &frac{delta L_t}{delta W_{aa}} = frac{delta L_t}{delta hat{y}_t}frac{delta hat{y}_t}{delta a_{t}}(frac{delta a_{t}}{delta W_{aa}} + frac{delta a_{t}}{delta a_{t-1}}frac{delta a_{t-1}}{delta W_{aa}} + …)\ &frac{delta L_t}{delta W_{ax}} = frac{delta L_3}{delta hat{y}_t}frac{delta hat{y}_t}{delta a_{t}}(frac{delta a_{t}}{delta W_{ax}} + frac{delta a_{t}}{delta a_{t-1}}frac{delta a_{t-1}}{delta W_{ax}} + …) end{aligned}$$

  • 對於任意時刻t對 (W_x)，(W_s) 求偏導的公式為：

[begin{aligned} &frac{delta L_t}{delta W_{aa}} = sum_{k=0}^{t}frac{delta L_t}{delta y_t}frac{delta y_t}{delta a_t}( prod_{j=k+1}^tfrac{delta a_j}{delta a_{j-1}} ) frac{delta a_k}{delta W_{aa}}\ &frac{delta L_t}{delta W_{aa}} = sum_{k=0}^{t}frac{delta L_t}{delta y_t}frac{delta y_t}{delta a_t}( prod_{j=k+1}^tfrac{delta a_j}{delta a_{j-1}} ) frac{delta a_k}{delta W_{aa}} end{aligned}]

  • 其中(frac{delta a_j}{delta a_{j-1}})和(frac{delta a_k}{delta W_{aa}})還存在(tanh’)的導數項，而(tanh’)的值域為((0, 1))。隨著時間步的增長，累乘項會趨於 0，出現梯度消失的問題

LSTM 如何解決 RNN 的梯度消失問題

  • RNN 的激活函數為 (tanh)，而 (tanh) 的導數取值範圍為 ([0, 1])，在時間上的反向傳播會存在時間上的梯度累乘項，時間步長了會導致梯度累乘而消失
  • LSTM 通過引入全局資訊流，在時間維度上引入殘差結構，殘差結構的引入就使得鏈式求導過程中引入了一個求和項，從反向傳播的求導來看，最多只有兩個激活函數的導數累乘，因此遠距離的梯度通常都可以正常傳播，減弱了梯度消失問題

怎樣增加 LSTM 的長距離特徵提取能力

  • Dilated RNN：Dilated CNN 為空洞卷積，Dilated RNN 則是在時間維度上空洞，淺層部分的為傳統 RNN，每個時間步都循環，深層的循環周期更長，增大時間維度上的「感受野」

個人為面試做的知識儲備，如有出錯，請大家指正，謝謝！

VirMach 便宜 VPS

QNews

QNews