Canny檢測演算法與實現
- 2020 年 3 月 14 日
- 筆記
1、原理
圖象邊緣就是影像顏色快速變化的位置,對於灰度影像來說,也就是灰度值有明顯變化的位置。影像邊緣資訊主要集中在高頻段,影像銳化或檢測邊緣實質就是高通濾波。數值微分可以求變化率,在影像上離散值求梯度,影像處理中有多種邊緣檢測(梯度)運算元,常用的包括普通一階差分,Robert運算元(交叉差分),Sobel運算元,二階拉普拉斯運算元等等,是基於尋找梯度強度。
Canny 邊緣檢測演算法是John F. Canny 於1986年開發出來的一個多級邊緣檢測演算法,也被很多人認為是邊緣檢測的 最優演算法, 最優邊緣檢測的三個主要評價標準是:
低錯誤率: 標識出儘可能多的實際邊緣,同時儘可能的減少雜訊產生的誤報。
高定位性: 標識出的邊緣要與影像中的實際邊緣儘可能接近。
最小響應: 影像中的邊緣只能標識一次。
Canny運算元求邊緣點具體演算法步驟如下:
1. 用高斯濾波器平滑影像.
2. 用一階偏導有限差分計算梯度幅值和方向.
3. 對梯度幅值進行非極大值抑制.
4. 用雙閾值演算法檢測和連接邊緣.
2、實現步驟
2.1、消除雜訊
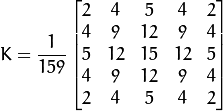
使用高斯平滑濾波器卷積降噪。下面顯示了一個 size = 5 的高斯內核示例:
2.2、計算梯度幅值和方向
按照Sobel濾波器的步驟,計算水平和垂直方向的差分Gx和Gy:
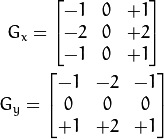
在vs中可以看到sobel像素值和形狀:

梯度幅值和方向為:

梯度方向近似到四個可能角度之一(一般 0, 45, 90, 135)。
2.3、非極大值抑制
非極大值抑制是指尋找像素點局部最大值。sobel運算元檢測出來的邊緣太粗了,我們需要抑制那些梯度不夠大的像素點,只保留最大的梯度,從而達到瘦邊的目的。沿著梯度方向,比較它前面和後面的梯度值,梯度不夠大的像素點很可能是某一條邊緣的過渡點,排除非邊緣像素,最後保留了一些細線。
在John Canny提出的Canny運算元的論文中,非最大值抑制就只是在0、90、45、135四個梯度方向上進行的,每個像素點梯度方向按照相近程度用這四個方向來代替。梯度向量的每個四分之一圓被45°線分成兩種情況,一種情況是傾向於水平,另一種傾向於豎直,一共 8 個方向。這種情況下,非最大值抑制所比較的相鄰兩個像素就是:
1) 0:左邊 和 右邊
2) 45:右上 和 左下
3) 90:上邊 和 下邊
4)135:左上 和 右下
這樣做的好處是簡單,但是這種簡化的方法無法達到最好的效果,因為自然影像中的邊緣梯度方向不一定是沿著這四個方向的,即梯度方向的線並沒有落在8鄰域坐標點上。因此,就有很大的必要進行插值,找出在一個像素點上最能吻合其所在梯度方向的兩側的像素值。
如果|gx|>|gy|,這說明該點的梯度方向更靠近X軸方向,所以g2和g4則在C的左右,我們可以用下面來說明這兩種情況(方向相同和方向不同):
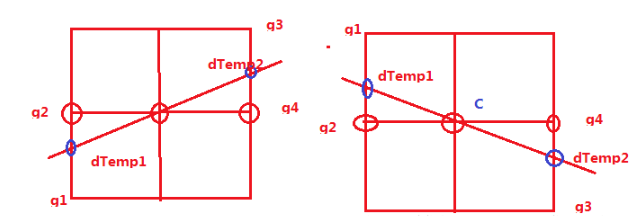
可以使用插值計算出真實梯度值:

其中,插值計算方式為:dTemp1 = weight*g1 + (1-weight)*g2; dTemp2 = weight*g3 + (1-weight)*g4;

Matlab使用非常有技巧的方式來計算方向,如下不僅做了dx、dy的大小判斷還做了方向的判定。
witch direction case 1 idx = find((iy<=0 & ix>-iy) | (iy>=0 & ix<-iy)); case 2 idx = find((ix>0 & -iy>=ix) | (ix<0 & -iy<=ix)); case 3 idx = find((ix<=0 & ix>iy) | (ix>=0 & ix<iy)); case 4 idx = find((iy<0 & ix<=iy) | (iy>0 & ix>=iy)); end
2.4、雙閾值檢測和區域連通
最後一步,Canny 使用了滯後閾值,滯後閾值需要兩個閾值(高閾值和低閾值)。如果邊緣像素的梯度值高於高閾值,則將其標記為強邊緣像素;如果邊緣像素的梯度值小於高閾值並且大於低閾值,則將其標記為弱邊緣像素;如果邊緣像素的梯度值小於低閾值,則會被抑制。閾值的選擇取決於給定輸入影像的內容。Canny 推薦的 高:低 閾值比在 2:1 到3:1之間。
3、程式碼實現
3.1 計算梯度
/* * Sobel 梯度計算 */ Mat gradients(Mat &img, Mat &sobel) { int W = img.cols; int H = img.rows; Mat dx = Mat_<int>(img.size()); int border = (int)sobel.rows / 2; for (int r = border; r < H - border; r++) { for (int c = border; c < W - border; c++) { float tmp = 0; for (int i = -border; i <= border; i++) { for (int j = -border; j <= border; j++) { tmp += (int)img.data[(r + i)*W + c + j] * sobel.at<int>(i + border, j + border); } } dx.at<int>(r, c) = tmp; } } return dx; }
3.2計算非極大值抑制(詳細推導過程見參考文獻文章)
/* fucntion: non-maximum suppression input: pMag: pointer to Magnitude, pGradX: gradient of x-direction pGradY: gradient of y-direction sz: size of pMag (width = size.cx, height = size.cy) limit: limitation output: pNSRst: result of non-maximum suppression */ void NonMaxSuppress(int *pMag, int * pGradX, int *pGradY, Size sz, int *pNSRst) { long x, y; int nPos; // the component of the gradient int gx, gy; // the temp varialbe int g1, g2, g3, g4; double weight; double dTemp, dTemp1, dTemp2; //設置影像邊緣為不可能的分界點 for (x = 0; x < sz.width; x++) { pNSRst[x] = 0; pNSRst[(sz.height - 1)*sz.width + x] = 0; } for (y = 0; y < sz.height; y++) { pNSRst[y*sz.width] = 0; pNSRst[y*sz.width + sz.width - 1] = 0; } for (y = 1; y < sz.height - 1; y++) { for (x = 1; x < sz.width - 1; x++) { nPos = y * sz.width + x; // if pMag[nPos]==0, then nPos is not the edge point if (pMag[nPos] == 0) { pNSRst[nPos] = 0; } else { // the gradient of current point dTemp = pMag[nPos]; // x,y 方嚮導數 gx = pGradX[nPos]; gy = pGradY[nPos]; //如果方嚮導數y分量比x分量大,說明導數方向趨向於y分量 if (abs(gy) > abs(gx)) { // calculate the factor of interplation weight = fabs(gx) / fabs(gy); g2 = pMag[nPos - sz.width]; // 上一行 g4 = pMag[nPos + sz.width]; // 下一行 //如果x,y兩個方嚮導數的符號相同 //C 為當前像素,與g1-g4 的位置關係為: //g1 g2 // C // g4 g3 if (gx*gy > 0) { g1 = pMag[nPos - sz.width - 1]; g3 = pMag[nPos + sz.width + 1]; } //如果x,y兩個方向的方嚮導數方向相反 //C是當前像素,與g1-g4的關係為: // g2 g1 // C // g3 g4 else { g1 = pMag[nPos - sz.width + 1]; g3 = pMag[nPos + sz.width - 1]; } } else { //插值比例 weight = fabs(gy) / fabs(gx); g2 = pMag[nPos + 1]; //後一列 g4 = pMag[nPos - 1]; // 前一列 //如果x,y兩個方向的方嚮導數符號相同 //當前像素C與 g1-g4的關係為 // g3 // g4 C g2 // g1 if (gx * gy > 0) { g1 = pMag[nPos + sz.width + 1]; g3 = pMag[nPos - sz.width - 1]; } //如果x,y兩個方嚮導數的方向相反 // C與g1-g4的關係為 // g1 // g4 C g2 // g3 else { g1 = pMag[nPos - sz.width + 1]; g3 = pMag[nPos + sz.width - 1]; } } dTemp1 = weight * g1 + (1 - weight)*g2; dTemp2 = weight * g3 + (1 - weight)*g4; if(dTemp ) //當前像素的梯度是局部的最大值 //該點可能是邊界點 if (dTemp >= dTemp1 && dTemp >= dTemp2) { pNSRst[nPos] = dTemp; } else { //不可能是邊界點 pNSRst[nPos] = 0; } } } } }
3.3雙閾值檢測和邊緣連接
void duble_threshold(Mat &pMag, Mat &pThreadImg, float threshold) { double maxv; int * img_ptr = pMag.ptr<int>(0); uchar * dst_ptr = pThreadImg.ptr<uchar>(0); minMaxLoc(pMag, 0, &maxv, 0, 0); cout << "max" << maxv << endl; int TL = 0.333 * threshold *maxv; // 1/3 of TH int TH = threshold *maxv; int w = pMag.cols; int h = pMag.rows; for (int r = 1; r < pMag.rows; r++) { for (int c = 1; c < pMag.cols; c++) { int tmp = img_ptr[r*w + c]; if (tmp < TL) { dst_ptr[r*w + c] = 0; } else if (tmp >= TH) { dst_ptr[r*w + c] = 255; } else { bool connect = false; for(int i=-1; i<=1 && connect == false; i++) for (int j = -1; j <= 1 && connect == false; j++) { if (img_ptr[r + i, c + j] >= TH) { dst_ptr[r*w + c] = 255; connect = true; break; } else dst_ptr[r*w + c] = 0; } } } } }
4、測試結論
測試1:左側是原圖,右側是進行了sobel梯度計算和非極大值抑制後的圖。

可見右圖,在企鵝輪廓內部還有孤立的點,放大後如下圖。
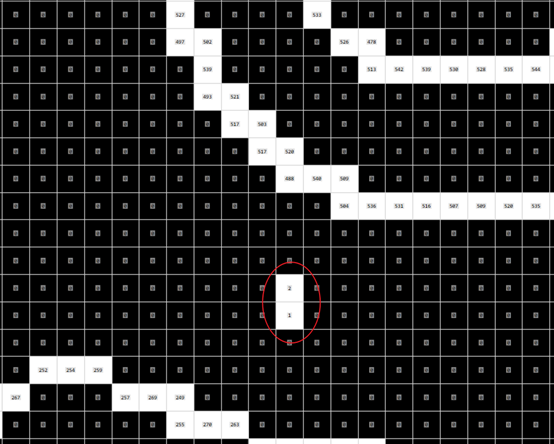
使用雙閾值限定後如下圖,內部點消失了。

測試2:選擇合適的閾值,影像中心的白色噪點可以消除。

測試3:
如下圖,圖2的雙閾值計算梯度後最大梯度360,圖3使用0.5倍高閾值,輪廓不連貫,可見閾值過高。改為0.2倍高閾值,結果如圖4,改善了輪廓缺失問題。
 5、參考文獻
5、參考文獻
1、《數字影像處理與機器視覺》,第二版。 張錚、徐超、任淑霞、韓海玲等編著。
2、Canny 邊緣檢測
3、Sobel運算元的數學基礎
http://blog.sciencenet.cn/blog-425437-1139187.html
4、Canny邊緣檢測
https://www.cnblogs.com/mmmmc/p/10524640.html
5、Canny運算元中的非極大值抑制(Non-Maximum Suppression)分析
https://blog.csdn.net/kezunhai/article/details/11620357
6、一種改進非極大值抑制的Canny邊緣檢測演算法
https://www.doc88.com/p-5174766661571.html
個人部落格,轉載請註明。
