歸併排序——一文吃透歸併和遞歸的思想和完整過程!(沒看懂請留言)
- 2020 年 3 月 13 日
- 筆記
凡是高效的排序演算法無疑都是採用了分治的策略。我們先來看一下什麼是分治的思想:
分治法,字面意思是“分而治之”,就是把一個複雜的問題分成多個相同或相似的子問題,再把子問題分成更小的子問題直到最後子問題可以簡單地直接求解,原問題的解即子問題的解的合併。即,分治法的思想是將原問題拆解成相同或者相似的子問題,直到子問題可以簡單的直接求解。
再來看一下遞歸所蘊含的思想:遞歸演算法的實質是把問題分解成規模縮小的同類問題的子問題,然後遞歸調用方法來表示問題的解。
也就是說:分治法是一種思想,分治法將問題拆解成子問題,但是分治法並沒有給出求解這些子問題的方法!而遞歸則是一種策略,遞歸可以用於解決這些同類的子問題。
歸併排序
關於歸併排序的Java程式碼和動圖演示,可以看下面這個部落格:https://www.cnblogs.com/l199616j/p/10604351.html
關於歸併排序的c++程式碼,可以看下面這篇部落格:https://blog.csdn.net/m0_38068229/article/details/81262282
下面,我將深入詳細的分析歸併遞歸的過程,並講解遞歸的詳細過程,並給出其中的要點:
我們以下面的數組為例子,用歸併排序的方法將上述數組排序。方法:遞歸:
9 7 8 4 1 6
首先,先表明在歸併排序中的第一個要點:將數組均等的一分為二.,這是什麼意思呢?,也就是我們不是將數組拆分成:
9 7 8 4 1 6 ——>9 7|8 4 1 6
儘管這也是將原問題分解成同類的子問題,但是這些子問題的規模不一致,但是請別搞錯了,這仍然是分治,而且我們仍然可以採用遞歸的方式繼續求解這些子問題。也就是說:分治與遞歸併不要求我們必須將子問題劃分成同等規模大小的問題(儘管這好像看起來劃分成同等規模似乎更為合理)。實際上,快速排序演算法就不是採用均分策略,但人家依然採用的是分治思想。因此,請記住:
歸併排序採用了遞歸的策略,但是數組均分策略是歸併的第一特點! 也就是,我們會將數組劃分成:
9 7 8 4 1 6 ——>9 7 8|4 1 6
那麼現在,我們問自己:現在這個子問題,我能解決嗎?很多人會回答?還不能…因為子問題還不夠小。
你之所以會這麼回答,也是因為經驗主義,這樣會限制你修改演算法的思維,假如我們將數組劃分的很小了,只要我們認為能解決了,那麼這個劃分的過程就可以結束了。比如上述我們可以採用O(n2)的演算法解決子問題,也不是不可以。所以,沒有任何演算法是完美的和絕對的。
那麼這裡,既然我們單純的討論遞歸的解決排序,我們自然可以繼續劃分上述子問題:
9 7 8 4 1 6 ——>9 7 8|4 1 6 -->9 7|8|4 1|6
這個時候,有人會問:這樣劃分,什麼時候是個頭呢?
此時,你應該問自己這麼一個問題:這個問題原本要解決什麼問題?答:對數組排序。那麼子問題的目標自然也是對數組排序,那麼分治問題的思想是,子問題解決了,原問題就可以解決;那麼子問題解決了是指什麼:子問題排好序了!繼續追問:什麼時候子問題排好序了:答案:子問題只剩下一個元素的時候,此時子數組自然就是有序的了。
即,劃分的終點是:
9 7 8 4 1 6 ——>9 7 8|4 1 6 -->9 7|8|4 1|6 -->9|7|8|4|1|6
用偽程式碼表示:
1 if(length == 1)//length為子數組的長度 2 return;
即:如果子數組的長度為1:那麼就可以返回。至此,遞歸的“遞”過程執行完畢,我們再來問自己一遍:遞歸的“遞”過程,完成了什麼?答:完成了將原問題劃分成子問題的過程,
並且最終的子問題都是有解的(對於這裡而言,都是有序的,而子問題有解是所有遞歸的終結條件,請記住)
那麼遞歸的“歸”過程呢?一言蔽之:反向求解每個子問題的解,直到求出原問題的解。
我們再來反向思考一下:如何考慮這個歸的過程。最後一步是:每個子數組只有一個元素,因此這個數組是有序的。那麼它的上一級是什麼?每個數組有兩個元素,這兩個元素是有序的。也就是說,我們進一步考慮一般問題就是:每個子數組上一組的問題就是:在兩個子數組都是有序的情況下,將這兩個有序的子數組合併成一個有序的子數組。這個就是歸併排序的第二要點。
偽程式碼表示為:
1 sort(orderdArray1,orderdarray2,array3) 2 { 3 ... 4 array3 is order; 5 }
我們用整個圖表示上述過程。

總結一下歸併排序的兩大特點:
- 在“遞”的過程中,對數組均等一分為二,再將子數組,一分為二….;
- 在“歸”的過程中,將這兩個有序的子數組合併成一個有序的子數組;
我們來看看具體的程式碼:
1 void MergeSort(vector<int>&data,int l,int r){ //使用遞歸對數組data從索引i到索引j之間的元素排序。 2 cout<<"the process of digui:"<<l<<","<<r<<endl; 3 if(r-l+1 == 1)//遞歸結束條件 4 return; 5 int mid = l+(r-l)/2; 6 MergeSort(data,l,mid);// 對前半部分繼續排序 7 MergeSort(data,mid+1,r);//對後半部分繼續排序 8 Sort(data,l,mid,r);//將兩個有序數組歸併成一個有序數組 9 }
其中,我們暫時並不給出Sort函數的具體實現,下文完整的程式碼中將會給出,這並不是我們要考慮的重點。很多人即使看了我之前的分析和上面的程式碼,仍然感覺有些模糊,原因在於,你對遞歸調用的恐懼和對其底層原理的不清楚,我們一步一步來:
遞歸而言,首先肯定 要給出遞歸結束條件,上述程式碼:r-l+1 ==1 即表述為:最終子數組只有一個元素時候,遞歸結束!
這裡有人要問了:為何這裡判斷之後直接return了,不是要給出最小子問題的解之後才返回嗎?比如求斐波那契數列第N項,不是返回前不是給出了第一項和第二項的值嗎?那麼,請別忘了排序的排序的子問題是將子數組排好序,那麼其終止條件是什麼:當然是將最小子數組排好序並返回。正如求斐波那契第N項時候,終止條件是:給出最開始的兩項並返回。從這點看,兩者在邏輯上是完全相同的。也就是,遞歸的結束條件一定是:原最小子問題的解!!!而這裡,當遞歸到最後一步時候,子數組只剩一下一個元素,而這個元素本身就是有序的,所以直接return即可(在其他問題中沒準需要你給出最小子問題的解)
遞歸結束條件討論完了,我們該討歸併的第二步,將原數組均分,一分為二,再將子數組,並求解每一部分子數組的正確序列;再將子數組一分為二,並且求解每一部分子數組的正確序列….!這裡面有很明顯的遞歸的意味,請深入體會。
我們再複述一遍上述過程:
遞歸的
- 將數組平均一份二位
- 求解前半部分的正確順序
- 求解後半部分的正確的順序
- 將排序好的前半部分和排序好的後半部分合併成一個排序好的大數組。
怎麼樣,有內味了吧。。。可能你還是會問:道理我都懂,可是這樣為何就能將原數組排序啊。問出這個問題說明,你對遞歸調用的過程並沒有一個清晰的認識,所以還是一知半解的。這裡,我將給出詳細分析,仔細看下圖:

下述,l與r的變化是對上述的解釋:
l r 9 7 8 4 1 6;mid1 = 2;(length≠1,繼續調用) l r 9 7 8 ;mid2 = 1;(length≠1,繼續調用) l r 9 7 ;mid3 = 0; (length≠1,繼續調用) l(r) 9 ;mid4 = 0;(length == 1,結束)結束
上述中,我故意將函數名字寫成了MergeSort1…等等,目的是為了說明:遞歸函數和普通函數本質是一致的,並無本質區別,當發生自己調用自己的時候,你完全可以認為,它調用了一個其他函數,只是這個函數好像和自己長得一模一樣,俗稱雙胞胎。並且和普通調用一樣,每個調用都會生成一個獨立的棧空間,因此,mid值並不是只有一個mid,而是在每個調用體里都有一個mid只存在自己的棧空間。
因此,這裡說明關於遞歸調用的兩點:
- 遞歸調用和普通函數調用並無區別,你可以把遞歸調用想成調用了一個和自己長得一樣的其他函數;
- 既然是函數調用,棧空間就是獨立的,哪怕它是遞歸調用,也是如此;
你可以按照我上面的思路,繼續分析,到底是怎樣完成排序的。我在此不作過多廢話廢話,非常建議畫圖領悟
下面貼出我的測試完整程式碼:
1 # include<iostream> 2 #include<vector> 3 using namespace std; 4 void Sort(vector<int>&,int ,int ,int ); 5 void MergeSort(vector<int>&,int ,int ); 6 int main() 7 { 8 vector<int> data; 9 for(int i = 1;i <= 8;i++) 10 data.push_back(8-i); 11 cout<<"the initial order:"; 12 for(int i = 0;i < 8;i++) 13 cout<<data[i]<<" "; 14 cout<<endl; 15 16 cout <<"strat sort..."<<endl; 17 MergeSort(data,0,7); 18 19 cout<<"the sorted order:"; 20 for(int i = 0;i < 8;i++) 21 cout<<data[i]<<" "; 22 cout<<endl; 23 24 system("pause"); 25 return 0; 26 } 27 void MergeSort(vector<int>&data,int l,int r){ //使用遞歸對數組data從索引i到索引j之間的元素排序。 28 cout<<"the process of digui:"<<l<<","<<r<<endl; 29 if(r-l+1 == 1)//遞歸結束條件 30 return; 31 int mid = l+(r-l)/2; 32 MergeSort(data,l,mid);// 對前半部分繼續排序 33 MergeSort(data,mid+1,r);//對後半部分繼續排序 34 Sort(data,l,mid,r);//將兩個有序數組歸併成一個有序數組 35 } 36 void Sort(vector<int>&data,int l,int mid,int r)//將兩個有序數組合併成一個有序數組,這是歸併排序的前提 37 { 38 vector<int> tmp(r-l+1);//一個臨時的空間,存放排序好的數組,最後將這個數組賦值給data[l]到data[r] 39 int i = l;//數組1索引 40 int j = mid+1;//數組2索引 41 int k = 0; 42 while((i<=mid) && (j <= r))//兩個索引都沒有超出邊界 43 { 44 if(data[i]<=data[j]) 45 tmp[k++] = data[i++]; 46 else 47 tmp[k++] = data[j++]; 48 } 49 while((i > mid) && (j <= r))//索引i超出數組1邊界(數組1訪問完畢),而索引j還未超出邊界 50 { 51 tmp[k++] = data[j++]; 52 } 53 while((j > r) && (i <= mid))//索引j超出數組2邊界(數組2訪問完畢),而索引i還未超出邊界
54 { 55 tmp[k++] = data[i++]; 56 } 57 for(int i = 0;i <r-l+1;i++) 58 data[l+i]= tmp[i]; //這一步對於data的索引極其容易出錯,需要清楚的是tmp總是從0開始,而data則是從左邊界l開始。 59 }
這裡稍微對有序數組合併成大數組的函數Sort()做一個解釋:
Sort(vector<int>&data,int l,int mid,int r)中data表示數組,表示已排序數組1的左邊界,mid表示已經排序數組1的右邊界(顯然mid+1表示已排序數組2的左邊界),r表示已經已排序數組的右邊界。
因為這兩個已經排序的數組其實都是原數組的一部分(地址空間沒變),所以我們要想將這兩個已經排好序的數組合併成一個數組,則需要一個額外的臨時空間,臨時空間用來快取重新排序的數組。最後將這個數組賦值到原數組。
我們的輸出結果是:
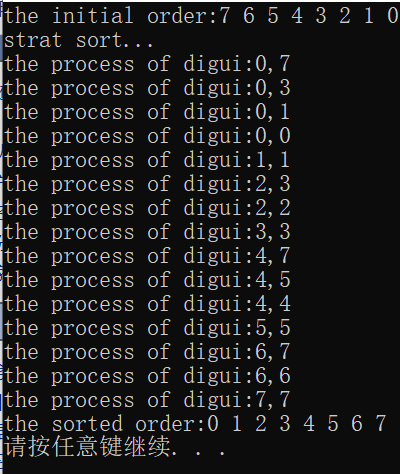
我在函數中設置了調用提醒,每次進行調用,我都會列印當前調用,從這裡你也畫出圖形可以分析遞歸的過程。
最後我們再次做一下總結:
歸併排序三大特點:
在“遞”的過程中,對數組均等一分為二,再將子數組,一分為二….;
在“歸”的過程中,將這兩個有序的子數組合併成一個有序的子數組
“歸過程每次合併數組的時候,要產生一個和原來兩個數組同樣大小空間的數組作為快取”,因此歸併排序的空間複雜度為O(n);
遞歸:
遞歸的結束返回永遠是最小子問題的解
遞歸調用就是普通函數調用,並無本質區別(每次調用有自己獨立的棧空間)
用遞歸思路解決問題,一定要實可提醒自己原問題是什麼,那麼子問題就是什麼!!


