AB實驗的高端玩法系列4- 實驗滲透低?用戶未被觸達?CACE/LATE
- 2020 年 3 月 12 日
- 筆記
CACE全稱Compiler Average Casual Effect或者Local Average Treatment Effect。在觀測數據中的應用需要和Instrument Variable結合來看,這裡我們只討論CACE的框架給隨機AB實驗提供的一些learning。你碰到過以下低實驗滲透低的情況么?
- 新功能入口很深,多數進組用戶並未真正使用新功能,在只能在用戶層隨機分流的條件下,如何計算新功能的收益
- 觸達策略,在發送觸達時進行隨機分組,但觸達過程存在損失,真正觸達的用戶佔比很小,如何計算觸達收益
背景
當然如果你的新策略滲透非常低,可能你的策略本身就需要調整。但就一些本身旨在提高少數用戶體驗的策略,或者策略初期試水的情況,CACE可能會比AB組的整體差異(ATE)更合適作為你實驗的衡量指標。因為它可能會告訴你策略對少部分用戶產生了顯著受益,你要做的只是去繼續迭代擴大用戶滲透而已。
ATE關注的是整個實驗組-對照組的收益,當然也會是策略全量上線後預估能拿到的對全用戶的收益。CACE估計的則是實驗對真正觸達的用戶預估產生的收益。注意這部分用戶的收益並不能泛化到全用戶,其一實驗對不同用戶的影響不同,其二策略的滲透率天然有限。往往滲透率越低對用戶的選擇性越強,觸達的用戶和整體用戶的差異更大,計算出的CACE更難泛化到全用戶上
CACE框架
讓我們回憶下ATE的計算, T是treatment,例如app增加的新功能, Y是outcome,比如用戶app使用時長,實驗效果一般通過ATE估計,因為這會最貼近實驗全量後在全用戶上拿到的最終受益
[ ATE = E(Y|T =1) – E(Y|T=0) ]
CACE額外加入了變數W實驗滲透,也就是用戶是否真正使用過新功能,CACE估計的是實驗對真正觸達的用戶產生的收益。如果你的實驗滲透100%那CACE=ATE,隨著實驗滲透的降低,理論上CACE會比ATE越來越高,因為部分用戶的收益被全體用戶稀釋。
說了這麼多CACE咋算嘞?別急先來展示2種錯誤卻經常被使用的方法
- Per-protocol Analysis = 實驗組滲透用戶 – 對照組全用戶
[ E(Y|Z=1, W(z=1)=1) – E(Y|Z=0) ] - As-treated Analysis = 實驗組滲透用戶 – 實驗組未滲透用戶
[ E(Y|Z=1, W(z=1)=1) – E(Y|Z=1, W(z=1)=0) ]
上面兩種方法都同時踩中了一個叫做Selection Bias的坑,也就是功能滲透本身是受到用戶行為/主觀意願影響,因此會存在用戶選擇。從而導致滲透用戶既不能代表全用戶,也會和未滲透用戶存在差異。真要在錯的裡面找個對的出來,Per-protocol一般更好一點。
CACE計算
用戶定義
CACE把用戶分為4類, compiler, never-taker, always-taker, defier,簡單說compiler是給葯就吃不給就不吃,never-taker是打死也不吃,always-taker是沒事就吃藥,defier是不給我葯我偏要吃。這四類人群可以通過W和Z進行定義如下
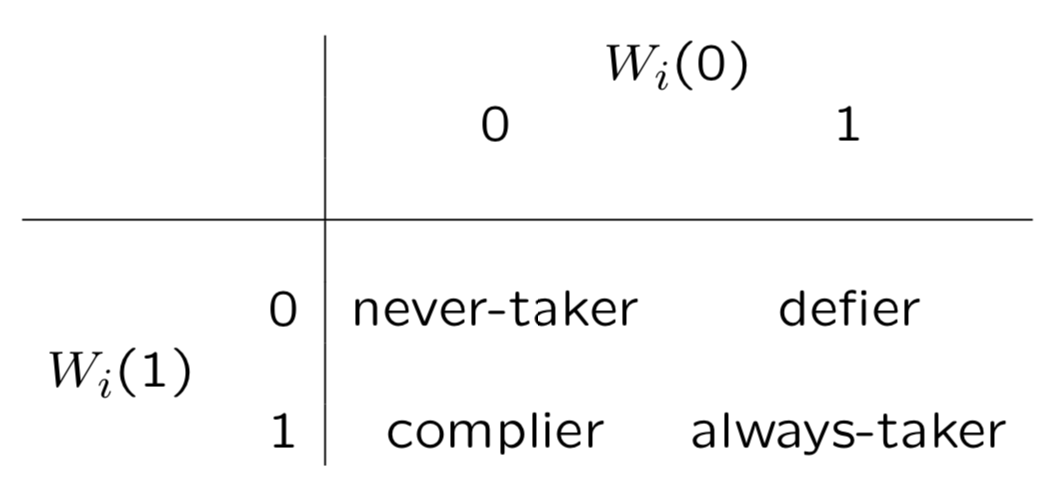
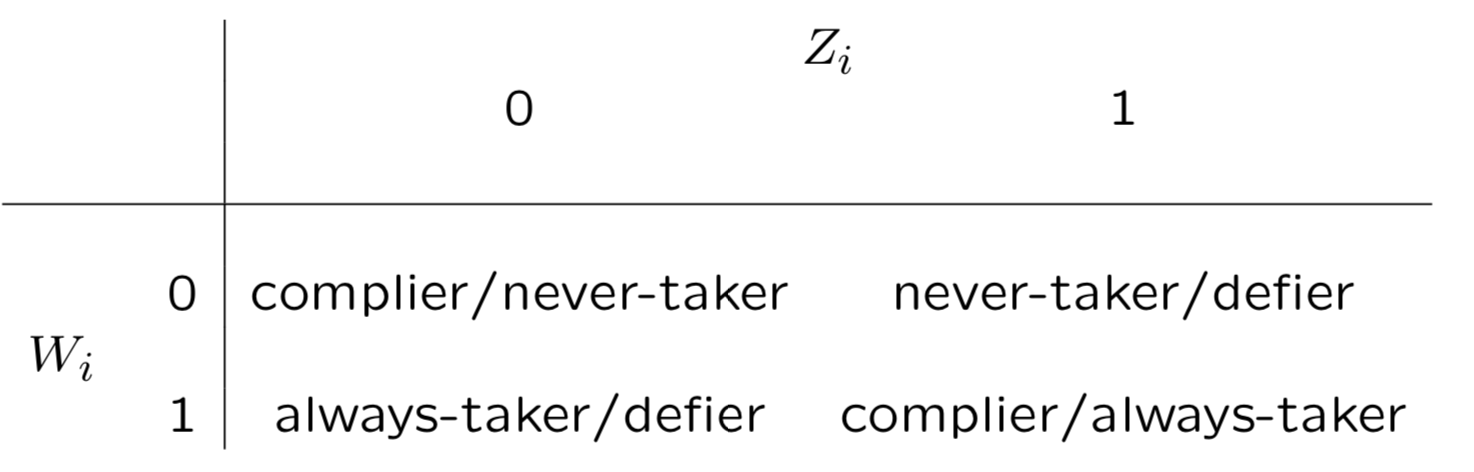
假設
要想CACE的計算成立,還需要滿足3條假設
1. Independence
這個在隨機AB實驗中一定成立,但在觀測數據中需要額外尋找Instrument variable這裡不予討論
[ Z_i perp (Y_i(0),Y_i(1),W_i(0),Y_i(1)) ]
2. Exclusion Restriction
這個假設即便在隨機AB實驗中也不一定成立,因此需要基於策略本身進行判斷,基本原則就是Treatment分組本身對用戶沒有影響,只有確實被Treatment滲透的用戶才受到影響。假設2保證了never-taker,always-taker在實驗組和對照組中的表現一致。
[ Y(z,w) = Y(z',w) ,,, text{for all z, $z'$,w} ]
印象中有看到過假設2不成立應該如何計算CACE的paper,不過還沒碰到過類似情況,以後有用到再加上吧。
3. Monotonicity/No-Defier
單調假設在絕大多數情況下都成立,也就是T對W是正效應,不存在Defier。 這時W和Z對應的人群會被簡化為以下,never-taker指向人群就是實驗組未滲透人群因此可以直接估計
[ W_i(1)>W_i(0) ]
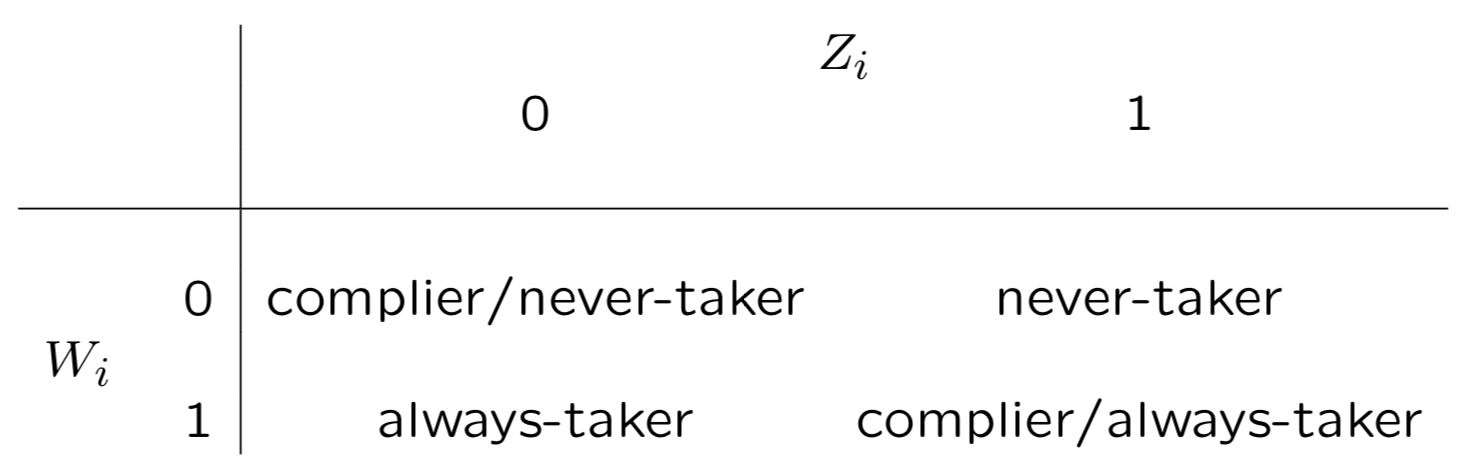
計算
隨機實驗的假設保證了compiler, always-taker, 和never-taker在對照組和實驗組中的佔比是相同的,因此我們可以直接計算出compiler, always-taker, never-taker在人群中的佔比,如下
[ begin{align} pi_a &= p(W(0)=W(1)=1) = E(W|Z=0)\ pi_c &= p(W(0)=0,W(1)=1) = E(W|Z=1) – E(W|Z=0)\ pi_n &= P(W(0)=W(1)=0) = 1- E(W|Z=1) \ end{align} ]
因為實驗組中未滲透用戶一定是never-taker, 對照組中滲透用戶一定是always-taker(在一些功能型隨機實驗中並不存在always-taker),因此這部分用戶的表現可以直接拿到
[ begin{align} E(Y|W=1,Z=0) &= E(Y(1)|always)\ E(Y|W=0,Z=1) &= E(Y(0)|never)\ end{align} ]
我們以此為突破口就可以計算得到compiler的CACE,先把對照組和實驗組的人群進行分解如下
[ begin{align} E(Y|Z=0) &= pi_a * E(Y(1)|always) + pi_n * E(Y(0)|never) + pi_c * E(Y(0)|compiler) \ E(Y|Z=1) &= pi_a * E(Y(1)|always) + pi_n * E(Y(0)|never) + pi_c * E(Y(1)|compiler) \ end{align} ]
很顯然AB組的差異只來源於compiler的差異,其實在沒有always taker的情況下, CACE只是按實驗組滲透等比的放大了組間收益而已
[ begin{align} CACE &= E(Y(1)|compiler) – E(Y(0)|compiler)\ &= frac{E(Y|Z=1)-E(Y|Z=0)}{pi_c}\ &= frac{E(Y|Z=1)-E(Y|Z=0)}{E(W|Z=1) – E(W|Z=0)} end{align} ]
對於顯著性的計算,我個人更偏向於只把CACE應用在原始ATE已經顯著的情況下,以避免針對一些沒有意義的波動數據進行分析,CACE只是用於估計滲透用戶的絕對收益。當然如果想要計算CACE的顯著性,可以用Bootstrap來拿到SE。當然因為CACE本身是ratio,也可以用更科學的方法來計算SE,具體細節可以參照Ref4。
用這個方法難免會被問到這部分用戶的收益能否泛化到全體用戶,理論上是不能的,但也不能一鎚子打死。一個比較簡單直觀的方法是去比較(E(Y(0)|compiler)),(E(Y(0)|always)),(E(Y(0)|never))之間是否存在顯著差異,差異越大,能泛化的可能一般是越小的。
對AB實驗的高端玩法感興趣??這裡
AB實驗的高端玩法系列1 – AB實驗人群定向/個體效果差異/HTE 論文github收藏
AB實驗的高端玩法系列2 – 更敏感的AB實驗, CUPED!
AB實驗的高端玩法系列3 – AB組不隨機?觀測試驗?Propensity Score
歡迎留言或評論~
Ref
- Imbens G. Methods for Estimating Treatment Effects IV: Instrumental Variables and Local Average Treatment Effects. Technical report, Lecture Notes 2, Local Average Treatment Effects, Impact Evaluation Network, Miami; 2010
- Complier average causal effect? Exploring what we learn from an RCT with participants who don’t do what they are told. 2017
- http://ec2-184-72-107-21.compute-1.amazonaws.com/_assets/files/events/slides_late
- Schochet, Peter Z. and Hanley Chiang (2009). Estimation and Identification of the Complier Average Causal Effect Parameter in Education RCTs (NCEE 2009-4040).


