(數據科學學習手札79)基於geopandas的空間數據分析——深入淺出分層設色
- 2020 年 3 月 9 日
- 筆記
本文對應程式碼和數據已上傳至我的
Github倉庫https://github.com/CNFeffery/DataScienceStudyNotes
1 簡介
通過前面的文章,我們已經對geopandas中的數據結構、坐標參考系、文件IO以及基礎可視化有了較為深入的學習,其中在基礎可視化那篇文章中我們提到了分層設色地圖,可以對與多邊形關聯的數值屬性進行分層,並分別映射不同的填充顏色,但只是開了個頭舉了個簡單的例子,實際數據可視化過程中的分層設色有一套策略方法。
作為基於geopandas的空間數據分析系列文章的第五篇,通過本文你將會學習到基於geopandas和機器學習的分層設色。
2 基於geopandas的分層設色
地區分布圖(Choropleth maps,又叫面量圖)作為可能是最常見的一種地理可視化方法,其核心是對某個與矢量面關聯的數值序列進行有意義的分層,並為這些分層選擇合適美觀的色彩,最後完成對地圖的著色,優點是美觀且直觀,即使對地理資訊一竅不通的人,也能通過顏色區分出不同面之間的同質性與異質性:
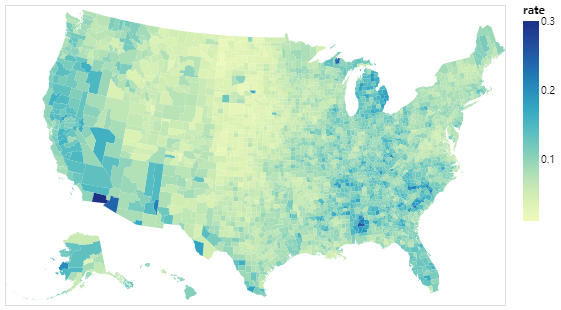
但同樣地,如果對數據分層採取的方法有失嚴謹沒有很好的遵循數據特點,會很容易讓看到圖的人產生出不正確的判斷,下面我們按照先分層,後設色的順序進行介紹。
2.1 基於mapclassify的數據分層
上一篇文章中我們提到過,,在geopandas.GeoDataFrame.plot()中,參數scheme對應的數據分層是基於第三方庫mapclassify實現的,因此要想對geopandas中的數據分層有深入的了解,我們就得先來了解一下mapclassify中的各種數據分層演算法,用到的數據是系列文章前幾期使用地滾瓜爛熟的新冠肺炎疫情數據,數據處理過程同上一篇文章,這裡不再解釋:

2.1.1 BoxPlot
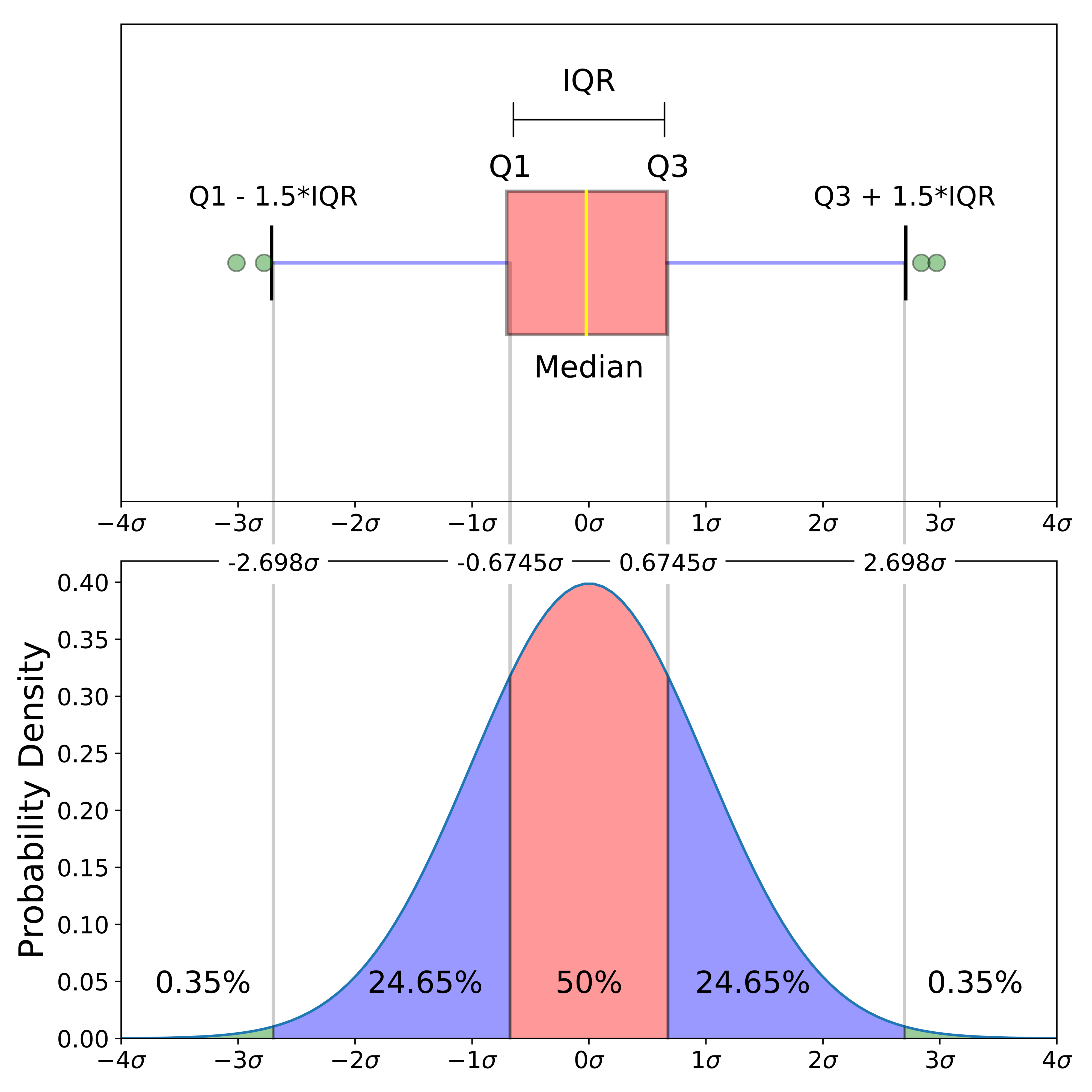
BoxPlot即箱線圖,是統計學中使用到的一種方法:對個數為(n)觀測數據從小到大進行排序,分別得到位置處於(0.25n)、(0.5n)以及(0.75n)的觀測值,稱為(Q_{1})、(Median)以及(Q_{3})(即第一四位數、中位數和第三四分位數),並定義(Q_{3}-Q_{1})為(IQR),以(Q_{1}-1.5IQR)為下限,以(Q3+1.5IQR)為上限,將小於下限或大於上限的觀測值作為離群異常值,最後用影像的形式表達上述計算結果,如圖2的上圖,而圖2的下圖對應著概率估計,可以看出,箱線圖法實際上是基於概率估計的一種異常值剔除方法,因為離群值只有(0.0035*2=0.007)的概率會出現,即如果你想要找出數據中的異常高低值,BoxPlot是不錯的選擇:
在mapclassify中我們使用BoxPlot()來為數據實現箱線圖分層:
import mapclassify as mc # 對各省2020-03-08對應的累計確診數量進行分層 bp = mc.BoxPlot(temp['province_confirmedCount']) # 查看數據分層結果 bp
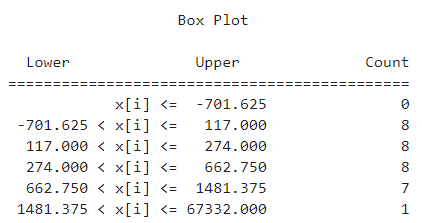
可以看出通過箱線圖法將數據分成了五類,其中異常值只有1個即為湖北省,下面我們配合geopandas來對上述結果進行可視化,和上一篇文章一樣,按照省級單位名稱連接我們的疫情數據與矢量數據:
接著對其進行可視化,在上一篇文章圖28的基礎上,將scheme參數改為BoxPlot,又因為箱線圖可以看作無監督問題,故分層數量k在這裡無效,刪去:
fig, ax = plt.subplots(figsize=(10, 10)) ax = data_with_geometry.to_crs(albers_proj).plot(ax=ax, column='province_confirmedCount', cmap='Reds', missing_kwds={ "color": "lightgrey", "edgecolor": "black", "hatch": "////", "label": "缺失值" }, legend=True, scheme='BoxPlot', legend_kwds={ 'loc': 'lower left', 'title': '確診數量分級', 'shadow': True }) ax = nine_lines.geometry.to_crs(albers_proj).plot(ax=ax, edgecolor='grey', linewidth=3, alpha=0.4) ax.axis('off') plt.suptitle('新型冠狀肺炎累計確診數量地區分布', fontsize=24) # 添加最高級別標題 plt.tight_layout(pad=4.5) # 調整不同標題之間間距 ax.text(-2800000, 1300000, '* 原始數據來源:丁香園,n其中台灣及香港數據缺失') # 添加數據說明 fig.savefig('圖6.png', dpi=300)
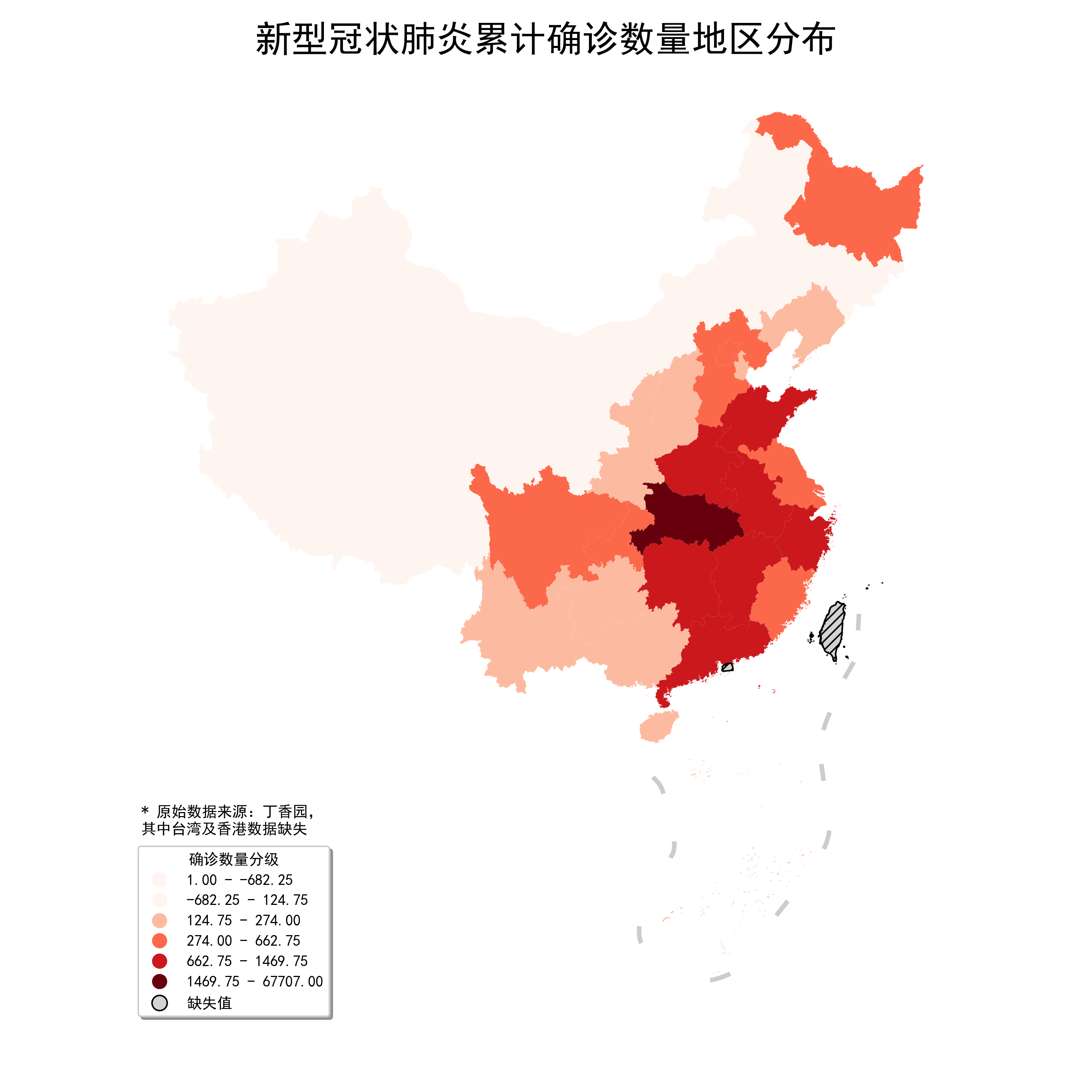
咋看起來沒問題,但是如果你仔細觀察左下角的圖例會發現前兩行範圍顏色是重複的,且數值範圍是錯亂的,這是geopandas.GeoDataFrame.plot()中涉及箱線圖法的一個小bug,遇到這種問題不用慌,如果你在上一篇文章中去我的Github倉庫查看過創作圖29對應的程式碼,一定會想到既然geopandas自身有bug,那我們用matplotlib中的mpatches和legend自定義圖例就可以啦,而為了自定義的圖例色彩與geopandas映射出的保持一致,我們需要額外使用到matplotlib中的get_cmap(cmap)來製作可獨立導出顏色的cmap方案實例,譬如我們這裡是Reds,就需要按照前面bp的有記錄數量的分層結果,從Reds中產生同樣5個檔次的顏色,具體操作過程如下:
import matplotlib.patches as mpatches fig, ax = plt.subplots(figsize=(10, 10)) ax = data_with_geometry.to_crs(albers_proj).plot(ax=ax, column='province_confirmedCount', cmap='Reds', missing_kwds={ "color": "lightgrey", "edgecolor": "black", "hatch": "////", "label": "缺失值" }, scheme='BoxPlot') handles, labels = ax.get_legend_handles_labels() #get existing legend item handles and labels ax = nine_lines.geometry.to_crs(albers_proj).plot(ax=ax, edgecolor='grey', linewidth=3, alpha=0.4) # 實例化cmap方案 cmap = plt.get_cmap('Reds') # 得到mapclassify中BoxPlot的數據分層點 bp = mc.BoxPlot(temp['province_confirmedCount']) bins = bp.bins # 製作圖例映射對象列表 LegendElement = [mpatches.Patch(facecolor=cmap(_*0.25), label=f'{int(max(bins[_], 0))} - {int(bins[_+1])}') for _ in range(5)] + [mpatches.Patch(facecolor='lightgrey', edgecolor='black', hatch='////', label='缺失值')] # 將製作好的圖例映射對象列表導入legend()中,並配置相關參數 ax.legend(handles = LegendElement, loc='lower left', fontsize=10, title='確診數量分級', shadow=True, borderpad=0.6) ax.axis('off') plt.suptitle('新型冠狀肺炎累計確診數量地區分布(截至2020年03月04日)', fontsize=24) # 添加最高級別標題 plt.title('數據分層方法:BoxPlot', fontsize=18) plt.tight_layout(pad=4.5) # 調整不同標題之間間距 ax.text(-2900000, 1250000, '* 原始數據來源:丁香園,n其中台灣及香港數據缺失') # 添加數據說明 fig.savefig('圖7.png', dpi=300)
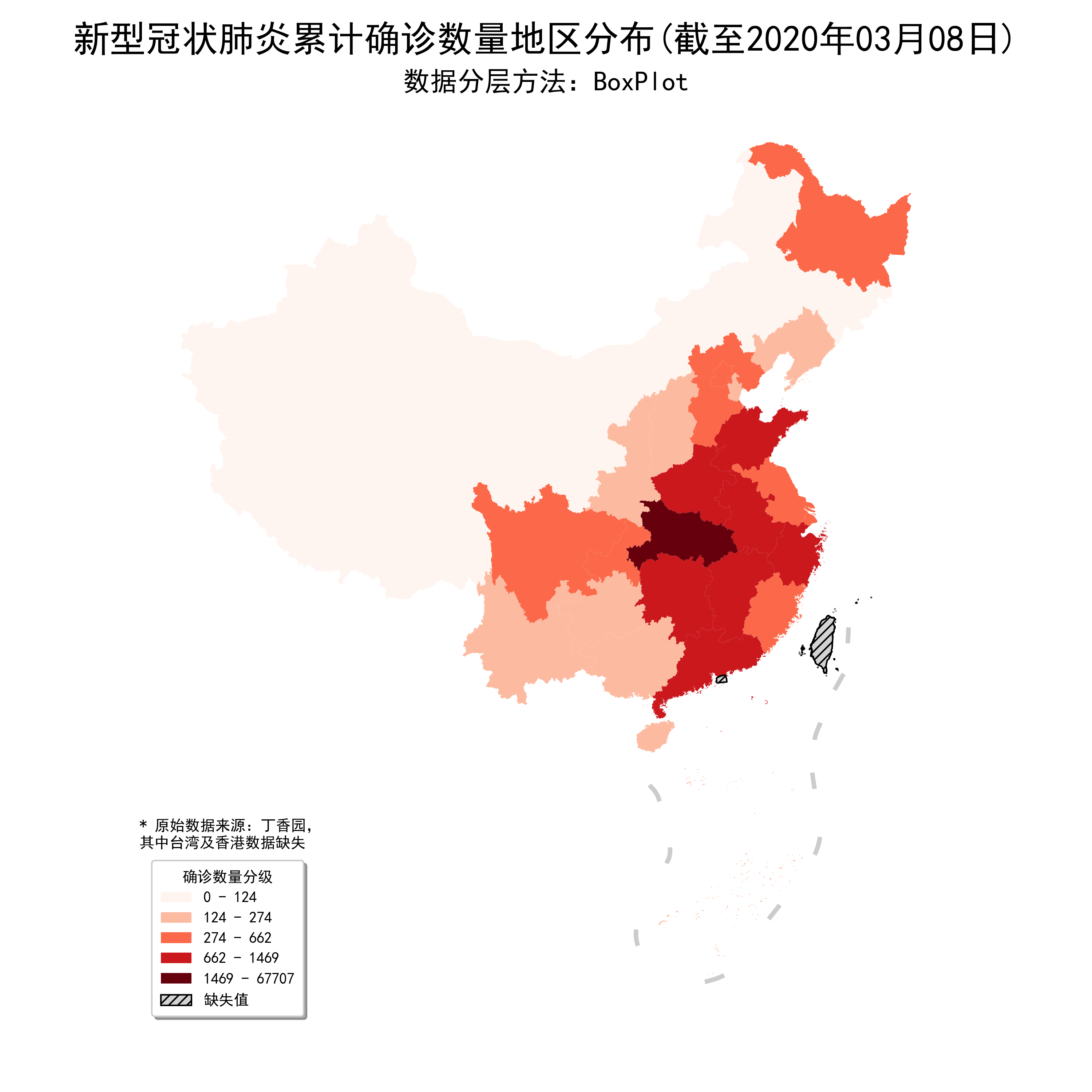
可以看到,通過自定義圖例的方式,雖然麻煩了一點,但是我們不僅修復了圖例的bug,還為其添加了更加完善的細節,如圖形修改為矩形,範圍修改為整數。
2.1.2 EqualInterval
EqualInterval即等間距,是最簡單的一種分層方法,它在原數據最小值與最大值間以等間距的方式劃分出k個層次,mapclassify中對應等間距法的類為EqualInterval():
bp = mc.EqualInterval(temp['province_confirmedCount']) # 查看數據分層結果 bp

可以看到對於分布非常不均勻的新冠肺炎確診數量數據來說,這種方法表現得十分糟糕,中間三個類都沒有記錄落入,如果使用這種方法強行繪圖,效果就會類似上一篇文章中地區分布圖部分,最開始那個糟糕的效果那樣只有湖北一個地方是最深的暗紅色,而其他地方皆為最淡的色階,這裡就不重複演示。
2.1.3 FisherJenks
在了解mapclassify中的FisherJenks之前,我們先來了解一下什麼是Jenks Natural Breaks:
- Jenks Natural Breaks
Jenks Natural Breaks旨在為1維數據計算合適的劃分點,使得不同組之間的差距儘可能大的同時組內差距儘可能小,其思路非常簡單,舉一個簡單的例子進行說明:
對於一組待分割的序列(X=[4, 5, 9, 10]),現在需要為其找到將原始數據分為(k=2)部分的方法,那麼實際上就有([4], [5, 9, 10])、([4, 5], [9, 10])以及([4, 5, 9],[10])這三種切分方法,現定義sum of squared deviations for array mean(簡稱SDAM):
[ SDAM=sum_{i=1}^{n}(X_{i}-bar{X})^{2} ]
以及針對每一種數據分層方法,在其分出的每一組(G_{i})上計算組內離差平方和並累加所有組的結果,定義為sum of squared deviations for class means(簡稱SDCM_ALL):
[ SDCM_ALL=sum_{i=1}^{k}sum_{j=1}^{|G_{i}|}(G_{ij}-bar{G_{i}})^2 ]
有了(SDAM)和(SDAM_ALL),現在對分組優劣定義一個評判指標goodness of variance fit(簡稱GVF),取值範圍為([0,1]),越高越好:
[ GVF=(SDAM-SCDM)/SDAM ]
這樣我們就可以對每一種分組方案進行評價,譬如對我們上面簡單的例子:
[ SDAM=(4-7)^2+(5-7)^2+(9-7)^2+(10-7)^2=26 \ SDCM_{1}=[(4-4)^2]+[(5-8)^2+(9-8)^2+(10-8)^2]=14 \ SDCM_{2}=[(4-4.5)^2+(5-4.5)^2]+[(9-9.5)^2+(10-9.5)^2]=1 \ SDCM_{3}=[(4-6)^2+(5-6)^2+(9-6)^2]+[(10-10)^2]=14 ]
則對應各種方案的GVF計算如下:
[ GVF_{1}=GVF_{3}=(26-14)/26=0.46 \ GVF_{2}=(26-1)/26=0.96 ]
可以看出第三種方案([4, 5], [9, 10])的分層方法效果最好,也與我們對數據的直觀感覺相貼合,這就是Jenks Natural Breaks的基本思路,但這種暴力遍歷所有分組方案的做法對數據數量及選擇分組的個數很敏感,尤其是對分組數量,一旦分組數量過於多,待篩選計算的方案數量就變成了天文數字,下面我來告訴大家為什麼:
定義長度為(n)的序列(X=[x_{1},x_{2},…,x_{n}])。且滿足(ileq{j})時(x_{i}leq{x_{j}}),即整個序列從小到大單調遞增,那麼將其分成(k)組的過程,可以分解為先選擇第一組,且為了保證右邊剩餘(k-1)個組每組至少有1個數據分配,則第一組有(n-k+1)種分配方式,而第一組包含的數字數量(n_{1})確定之後,剩餘(n-n_{1})個數據的繼續分組又可以視為獨立的遞歸分組過程,因此最終需要考慮的方案個數用公式表達起來有些複雜,但是換成電腦中的遞歸過程就變得一目了然,我經過思考和紙上的推演,寫出了下面所示的遞歸函數f(n, k)來實現方案總數的計算:
def f(n, k): # 若k退化為2,則顯然需要n - 1種方案,譬如4個數字分2組有3種方案 if k == 2: return n - 1 else: # 若k未退化為2,則繼續遞歸過程 return sum([f(n-_, k-1) for _ in range(1, n - k + 2)])有了這個遞歸函數,我們就可以來直觀的看一看為什麼不能選擇太多分組,首先我們對長度為100的序列分為5組試試:
f(100, 3) Out[11]: 4851可以看到待選擇的方案才4851個,還是很少的,那麼我們接下來將組數提高到5:
f(100, 5) Out[12]: 3764376發生了什麼?隨著遞歸深度的增大,待選擇方案數量一下子就提高到三百多萬個!再切換成7試一下:
f(100, 7) Out[13]: 1120529256 在跑上述程式碼時,明顯能感受到計算花費時間的激增,最終結果也達到驚人的11億多!看到這,我們就明白了,原始的Jenks Natural Breaks演算法雖然很有效,但如果以暴力遍歷的方式計算,其複雜度是難以應付日常需求的,為了對其進行優化,以在少量的計算時間內計算出儘可能靠譜的分組結果,一系列改良加速方法被提出,而mapclassify中的FisherJenks,即為jenks教授在論文Fisher, W. D., 1958, On grouping for maximum homogeneity.的基礎上提出的改良演算法,但這是一個很神秘的演算法,根據https://macwright.org/2013/02/18/literate-jenks.html 中的介紹,jenks教授的原始論文沒有留下數字化資料,一直為堪薩斯大學地理學系所私有,而隨著1996年jenks教授的離世,原論文需要到2072年版權才能到期公開,所以我們現在在各種GIS類軟體以及各種開源軟體包中使用到的fisher jenks演算法,均是對最初的一段Fortran程式碼的移植和改造,這也成了一段未解之謎,感興趣的讀者可以去https://stat.ethz.ch/pipermail/r-sig-geo/2006-March/000811.html 了解更多。
回到我們的主題,搞清楚了FisherJenks的計算目標之後,我們同樣利用mapclassify計算分層結果,其默認分層為5:
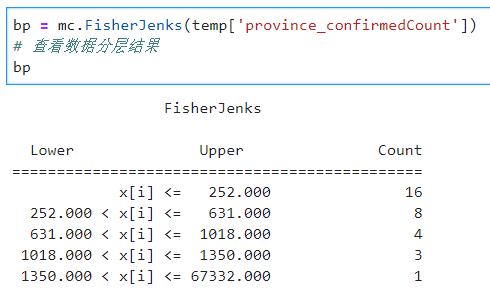
可以看到,在這種方式下,數據的分組較為合理,同樣將geopandas.GeoDataFrame.plot()中的參數設置為FisherJenks繪製出圖10:
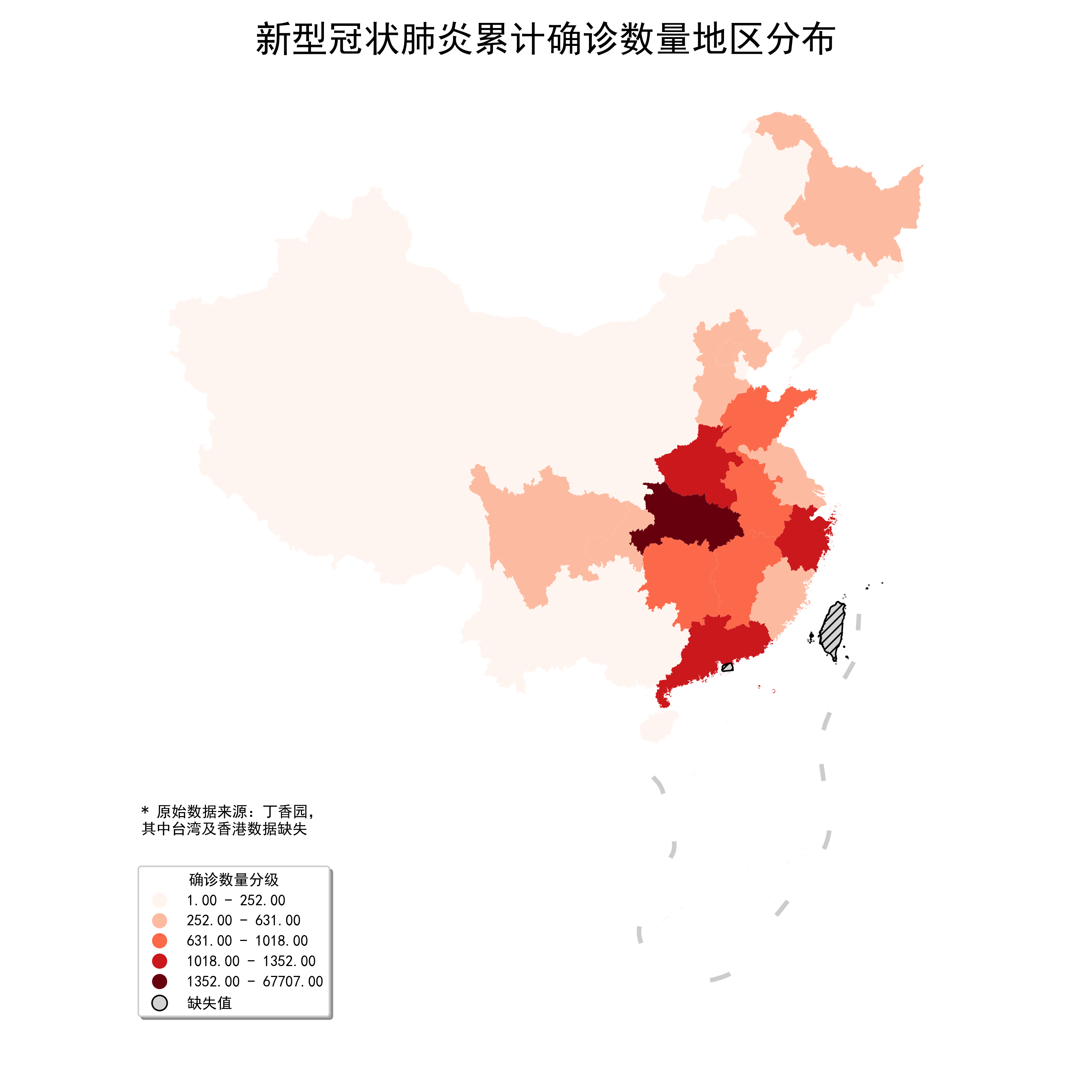
與BoxPlot相比差距還是比較明顯,處於第二級嚴重程度的省份只有河南、廣東及浙江,更貼近數據的自然層次結構。
2.1.4 NaturalBreaks
等下!上一小結中的FisherJenks不就是我們俗稱的自然斷點法嗎,怎麼又來了個NaturalBreaks?其實我在翻看mapclassify的官方文檔看到這裡時,也很疑惑,於是我仔細研究了NaturalBreaks對應的源程式碼,追根溯源,WHAT?,竟然是k-mean演算法,而且直接調用的scikit-learn的KMEANS。。。
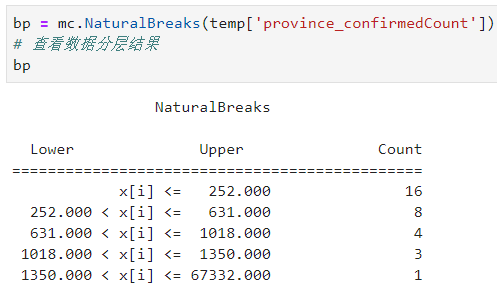
不過也可以理解,畢竟k-means就是在找數據中組內相似度儘可能高且組間差異盡量大的簇,關於k-means我想我就不需要贅述了,畢竟是最基礎的數據挖掘演算法之一,而scikit-learn里默認的KMEANS使用的k-means++初始方式,只是在原始k-means基礎上,修改了後續初始點的概率密度,使得k-means演算法更加魯棒穩定,下面直接來看NaturalBreaks的數據分層結果:
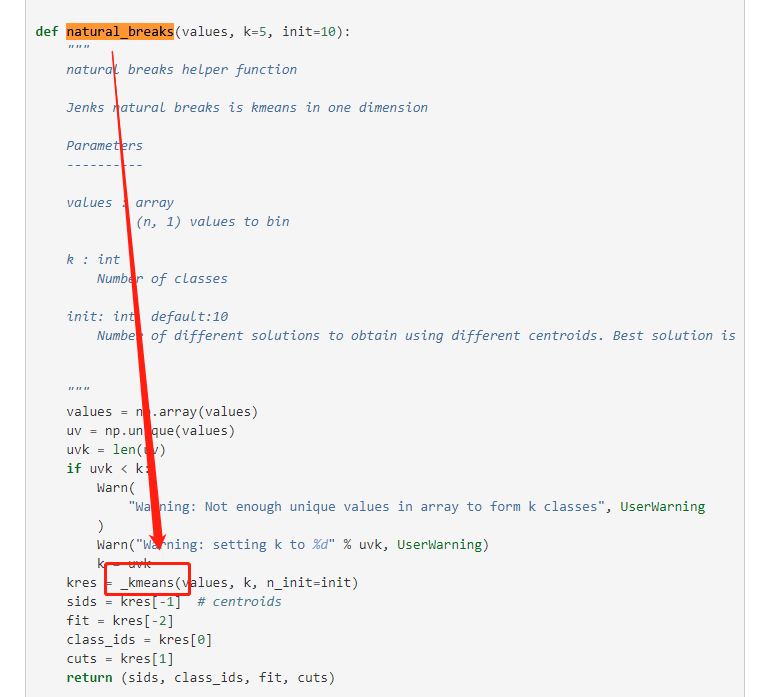
和FisherJenks的結果竟然一樣,但如果你多運行幾次會發現這個結果不是完全固定的,由於k-means隨機初始迭代起點,因此不同次運行的結果可能會有輕微差別(圖13),在數據量很大時,基於快速聚類法的NaturalBreaks是較為理想的數據分層選擇:
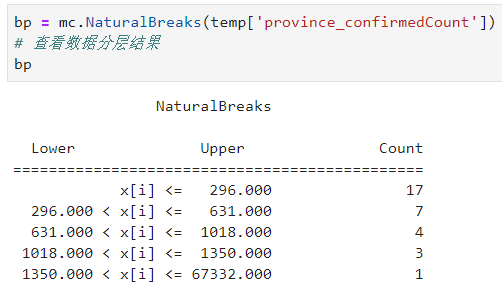
配合geopandas繪圖只需要把scheme參數修改為NaturalBreaks即可,因為跟FisherJenks類似,這裡就不再贅述。
2.1.5 JenksCaspall
mapclassify中的JenksCaspall本質上為k-medians聚類,其首先根據分層層數(k)在數據中找到(k-1)個分位數點,將原始數據等分為數量儘可能相同的(k)份並以這(k)份數據的中位數作為各自的初始點,接著基於k-medians的思想,迭代計算為每個樣本點找到與其距離更近的中位數點,並以此重新劃分分層以及重新計算各分層中位數點,直至每個數據對應的分層標籤不再變化,再將每個分層中數據的最大值作為間斷點,下面我們從mapclassify源程式碼中抽出該部分程式碼,對其迭代過程可視化,具體的程式碼較多,請在文章開頭的Github倉庫中對應本文路徑下查看:
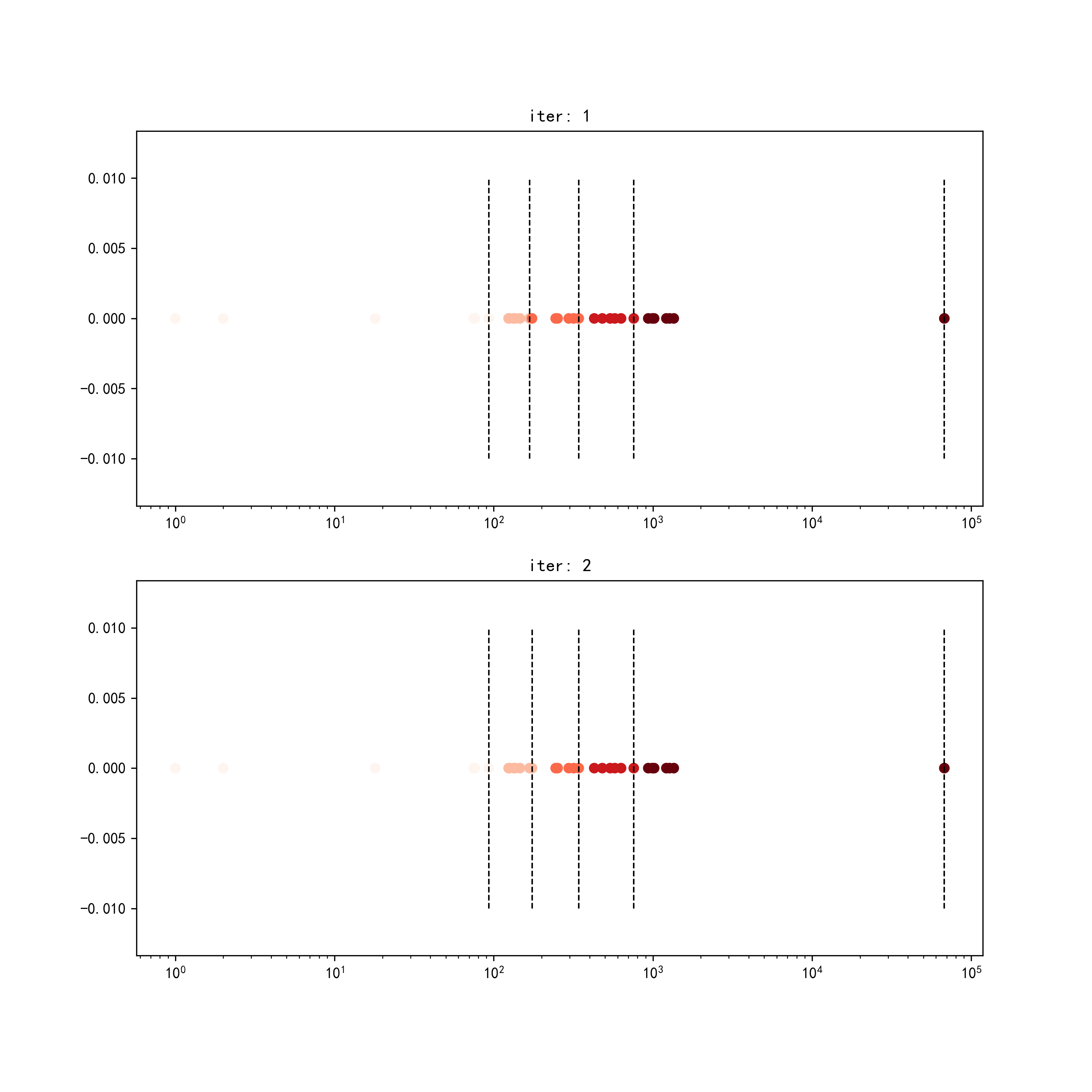
其中顏色區分對應迭代輪次的數據分層歸屬,虛線代表對應迭代輪次的間斷點,仔細可以看出在迭代過程中數據分層的變化情況。
用JenksCaspall數據分層出來的結果,無論數據分布如何,每個分層內部的數據個數都較為均勻,下面我們用JenksCaspall來劃分省份疫情嚴重情況:
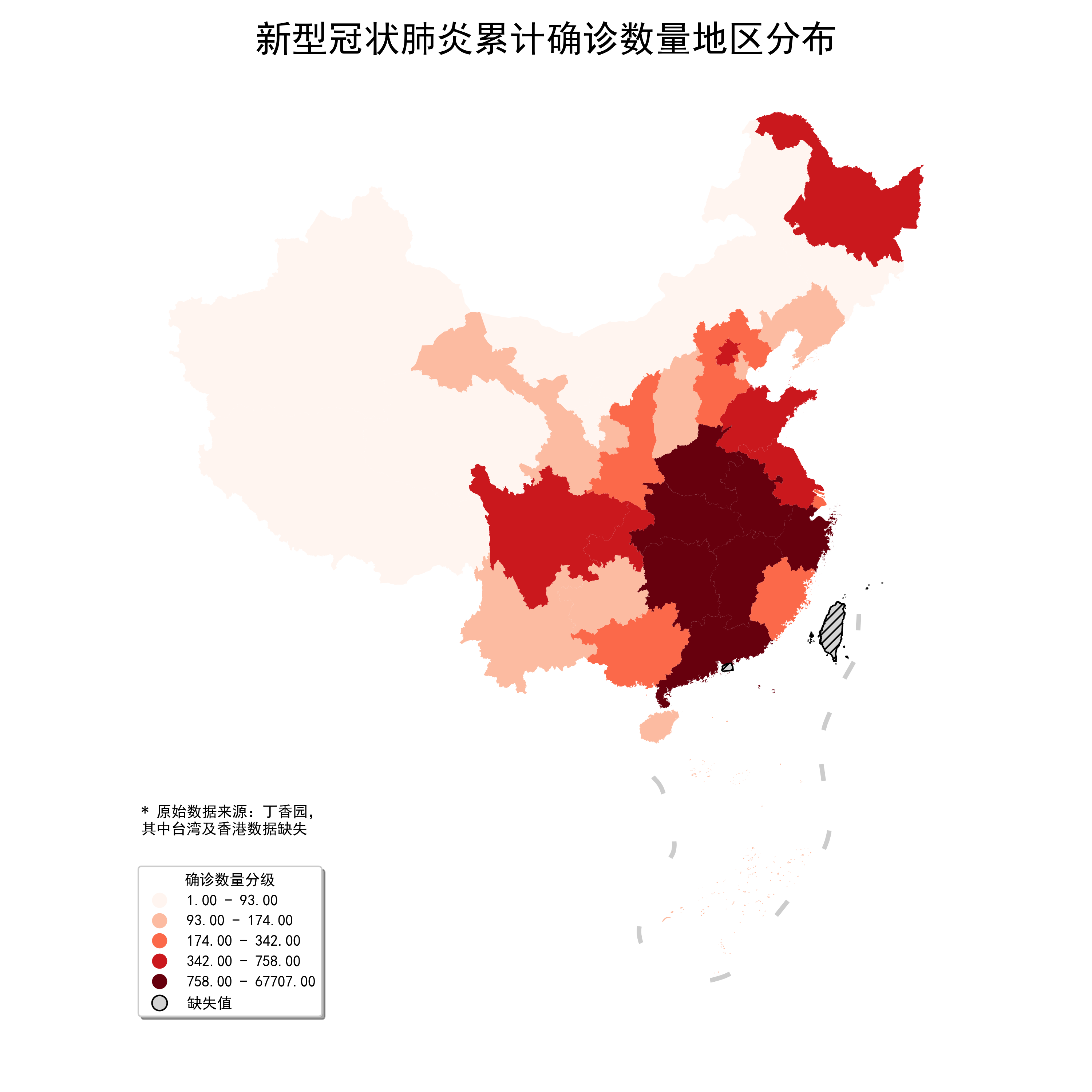
可以看到被分到最嚴重級別的不再只有湖北省,當你希望數據分層個數較為均勻時,JenksCaspall是個不錯的選擇。
2.1.6 HeadTailBreaks
HeadTailBreaks是一種較為嶄新的數據分層方法,出自Head/Tail Breaks: A New Classification Scheme for Data with a Heavy-Tailed Distribution(https://www.tandfonline.com/doi/abs/10.1080/00330124.2012.700499),專門用於對具有重尾特點的數據進行分層,所謂重尾即在整個數據中,較小的值數量往往較多,而最大的位於頭部的值數量很少,其數據分布呈現出「尾重頭輕」的特點:
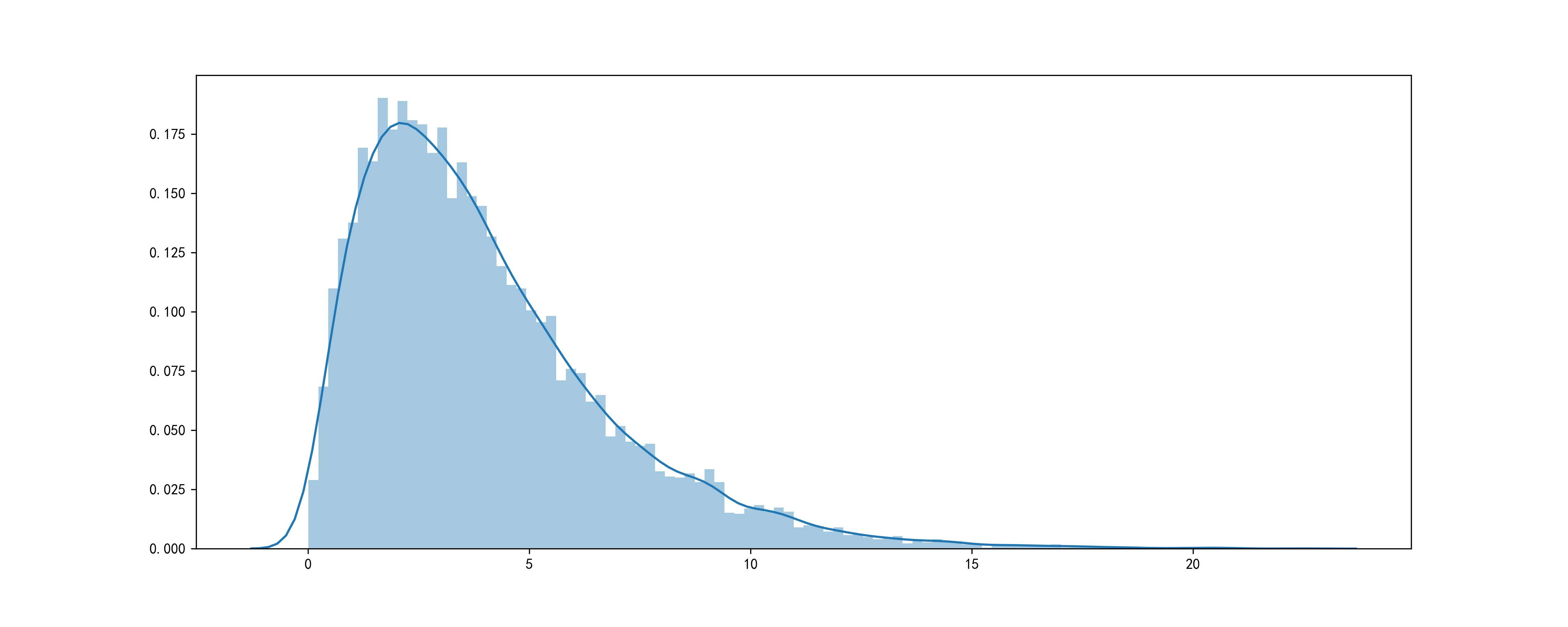
這種典型如人口密度分布數據,數值較低的點往往數量眾多,聚集在尾部,形成重尾,HeadTailBreaks的優點是可以盡量在地區分布圖中真實反映原始數據的分布特點,如圖17(https://sites.google.com/site/thepowerofcartography/head-tail-breaks),左邊是FisherJenks,右邊是HeadTailBreaks,可以看出,右圖相對於左圖更好地體現了原始數據的重尾特點,最淺色的圖斑數量明顯多於次淺色的圖斑:
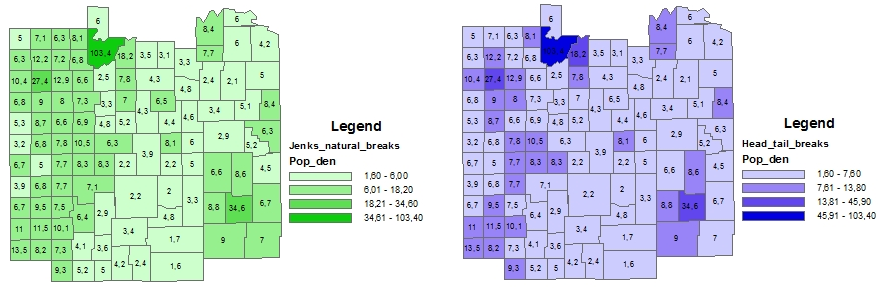
在geopandas中使用時傳入scheme='HeadTailBreaks'即可(由於新冠肺炎各省份確診數量數據尾部和頭部最大值之間沒有較為連續的中間值過渡,不太適合用此方法故不作演示)。
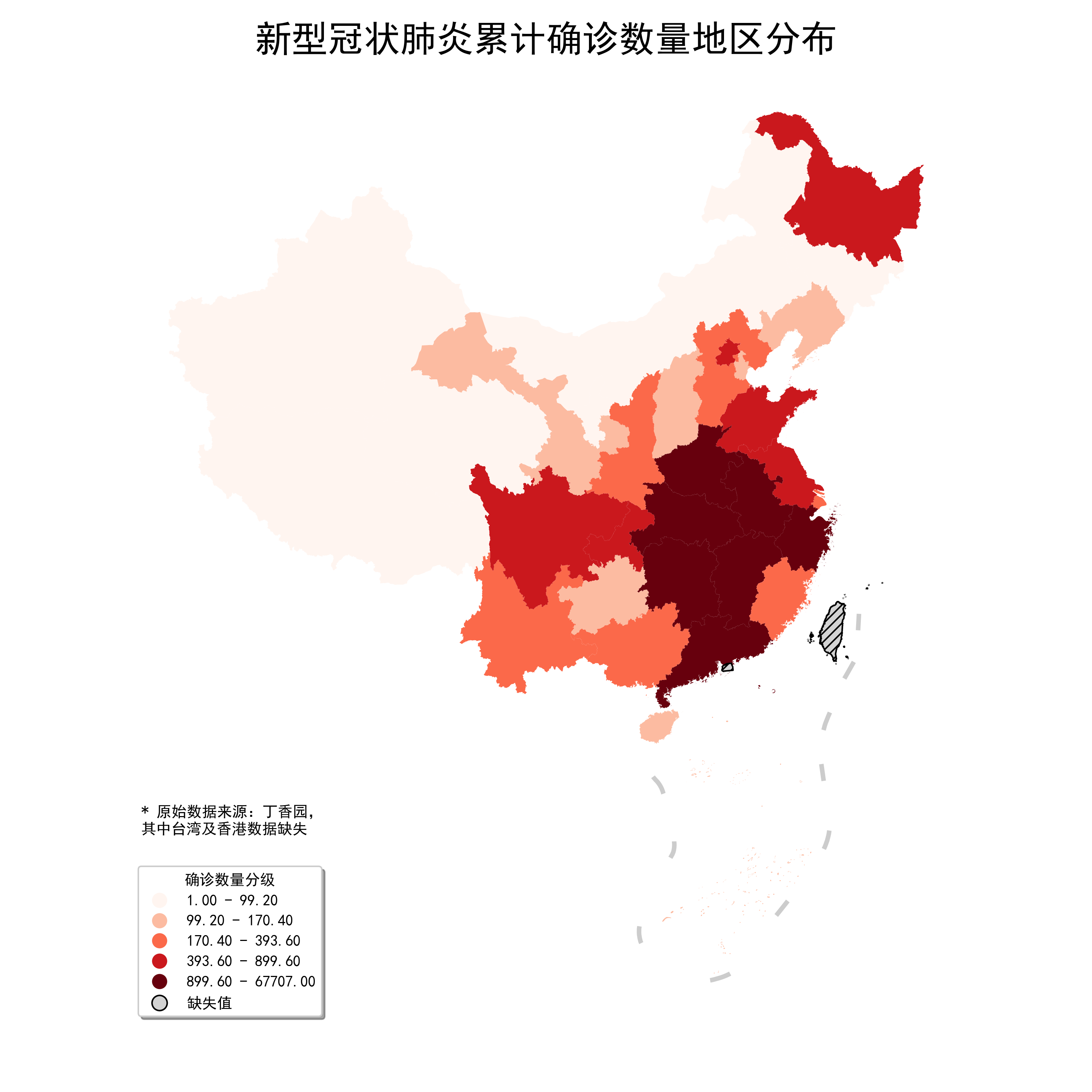
2.1.7 Quantiles
Quantiles即分位數,原理很簡單,根據分位數點對原數據進行等分:
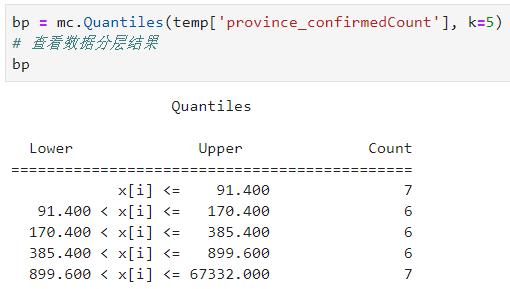
利用Quantiles對確診數量分組可視化:
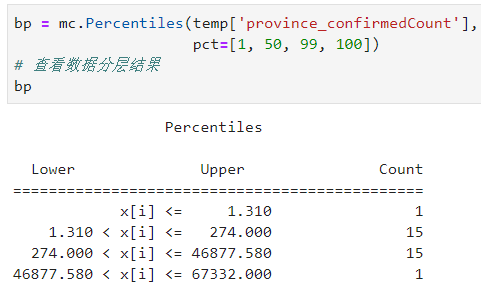
2.1.8 Percentiles
同樣是使用分位數對數據進行分層,Percentiles提供了參數pct以允許用戶以百分位數的形式傳入自定義分隔點,譬如我們將[1, 50, 99, 100]作為pct的傳入值,則分組結果如下:
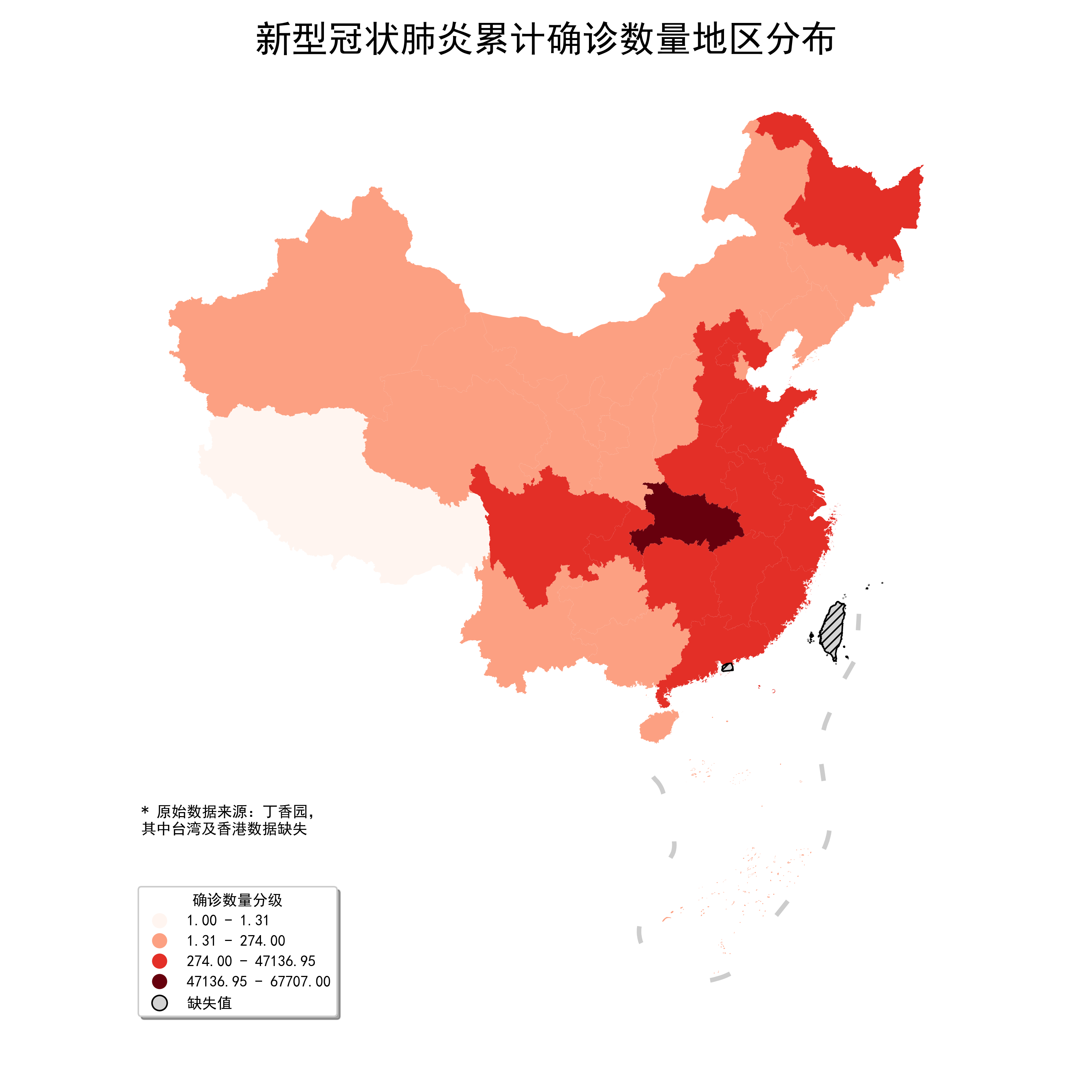
每個傳入的百分位點其左邊到上一個分隔點為止,包括其本身,將被分到同一組,對應的影像如圖21,在geopandas中使用時除了設置scheme='Percentiles'之外,還要在另一個字典型參數classification_kwds中傳入{'pct': 百分位數列表}:
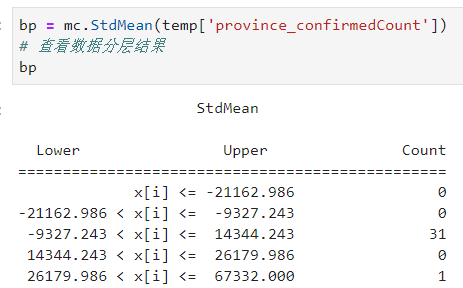
2.1.9 StdMean
StdMean的思想類似前面的箱線圖,不同的是箱線圖屬於非參數方法,而StdMean建立在正態分布為基礎的經驗法則之上,即對於正態分布而言,68%的數據將分布在距離均值1個標準差之內,95%的數據在2個標準差之內,99.7%的數據在3個標準差之內,即對原始數據標準化之後,根據距離樣本均值的不同標準差範圍來劃分數據,mapclassify中的StdMean默認按照[-2, -1, 1, 2]來劃分:
2.1.10 UserDefined
關於數據分層最後要介紹的是自定義分層,即按照用戶輸入的分隔點來自由劃分數據集,譬如我們按照新浪新聞疫情地圖的劃分方式:
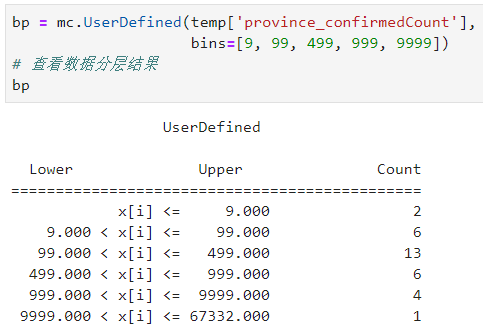
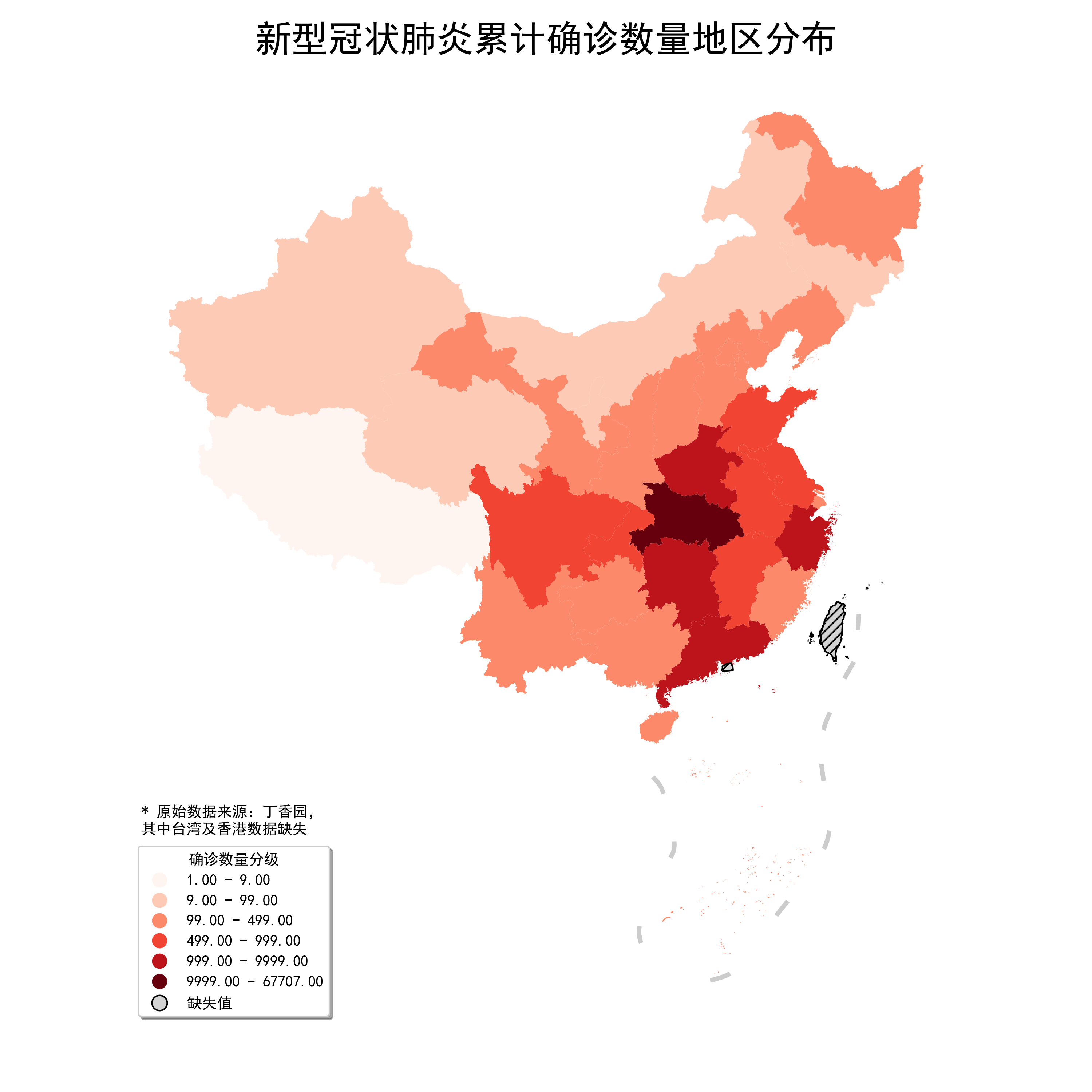
結合geopandas使用時除了設置scheme='UserDefined'以外,還要設置classification_kwds中的bins=分隔點列表:
fig, ax = plt.subplots(figsize=(10, 10)) ax = data_with_geometry.to_crs(albers_proj).plot(ax=ax, column='province_confirmedCount', cmap='Reds', missing_kwds={ "color": "lightgrey", "edgecolor": "black", "hatch": "////", "label": "缺失值" }, legend=True, scheme='UserDefined', classification_kwds={ 'bins': [9, 99, 499, 999, 9999] }, legend_kwds={ 'loc': 'lower left', 'title': '確診數量分級', 'shadow': True }) ax = nine_lines.geometry.to_crs(albers_proj).plot(ax=ax, edgecolor='grey', linewidth=3, alpha=0.4) ax.axis('off') plt.suptitle('新型冠狀肺炎累計確診數量地區分布', fontsize=24) # 添加最高級別標題 plt.tight_layout(pad=4.5) # 調整不同標題之間間距 ax.text(-2800000, 1300000, '* 原始數據來源:丁香園,n其中台灣及香港數據缺失') # 添加數據說明 fig.savefig('圖24.png', dpi=300)
2.2 色彩方案的選擇
前面已經詳細介紹了數據分層常用的各種方法及使用場景,「分層」的部分做完之後,就到了設色的部分,其實色彩搭配是比較主觀的事情,但想要自己創造出美觀合理的配色方案並不是容易的事情,下面我們來介紹兩種選擇配色方案的方法。
2.2.1 基於palettable的配色
下面我要給大家介紹的Python第三方庫palettable在我之前關於詞雲圖的一篇文章中介紹stylecloud時介紹過,是專門幫助我們為可視化作品配色的。
palettable不依賴其他三方庫,純Python實現,其強大之處在於內置了數量驚人的經典配色方案,囊括了CartoColors、cmocean、Colorbrewer2、Cubehelix、Light & Bartlein、matplotlib、MyCarta、Scientific、Tableau以及The Wes Anderson Palettes blog中的大量經典配色方案:
palettable.cartocolors.divergingpalettable.cartocolors.qualitativepalettable.cartocolors.sequentialpalettable.cmocean.divergingpalettable.cmocean.sequentialpalettable.colorbrewer.divergingpalettable.colorbrewer.qualitativepalettable.colorbrewer.sequentialpalettable.lightbartlein.divergingpalettable.lightbartlein.sequentialpalettable.matplotlibpalettable.mycartapalettable.scientific.divergingpalettable.scientific.sequentialpalettable.tableaupalettable.wesanderson
使用起來非常簡單,譬如如果我們想要使用palettable.cmocean.sequential中的色彩,其中cmocean表示色彩來源,sequential表示連續型色彩,就可以先在對應的示例網頁下查看所有方案:
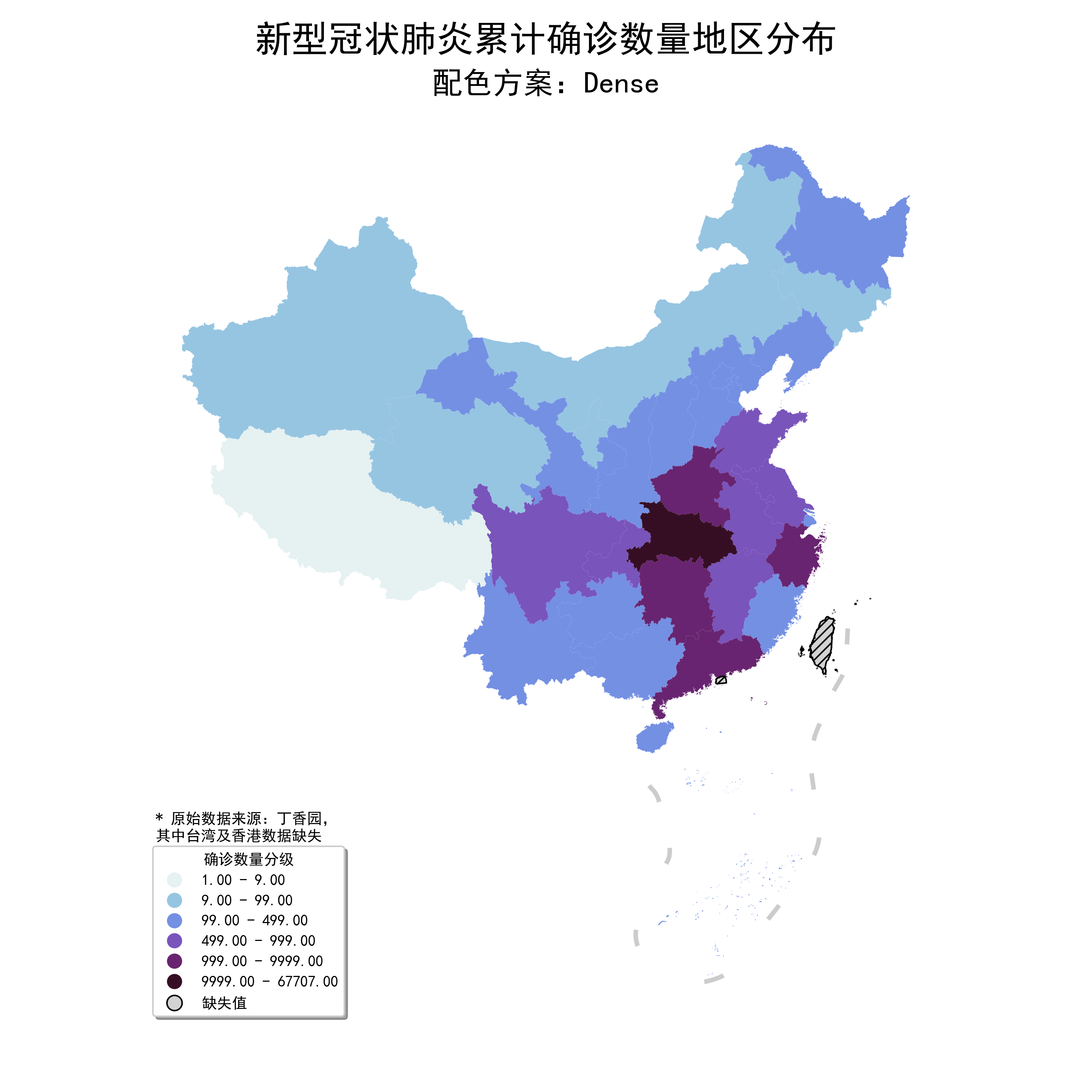
比如我對其中的Dense方案很中意:
就可以按照如下方式,先從palettable中導入對應顏色,譬如我們導入Dense_20,20表示其自帶的離散色彩數量,並查看其自帶的離散色彩RGB值、離散色盤以及連續色盤示例:
from palettable.cmocean.sequential import Dense_20 from pprint import pprint print('對應離散顏色:') pprint(Dense_20.colors) print('離散:') Dense_20.show_discrete_image() print('連續:') Dense_20.show_continuous_image()
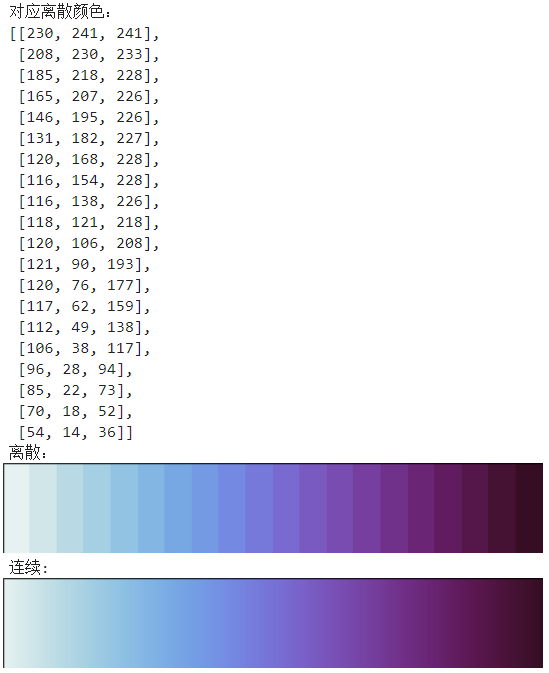
使用.mpl_colormap將其轉換為matplotlib可接受的cmap數據結構,作為cmap參數值傳入繪圖部分即可:
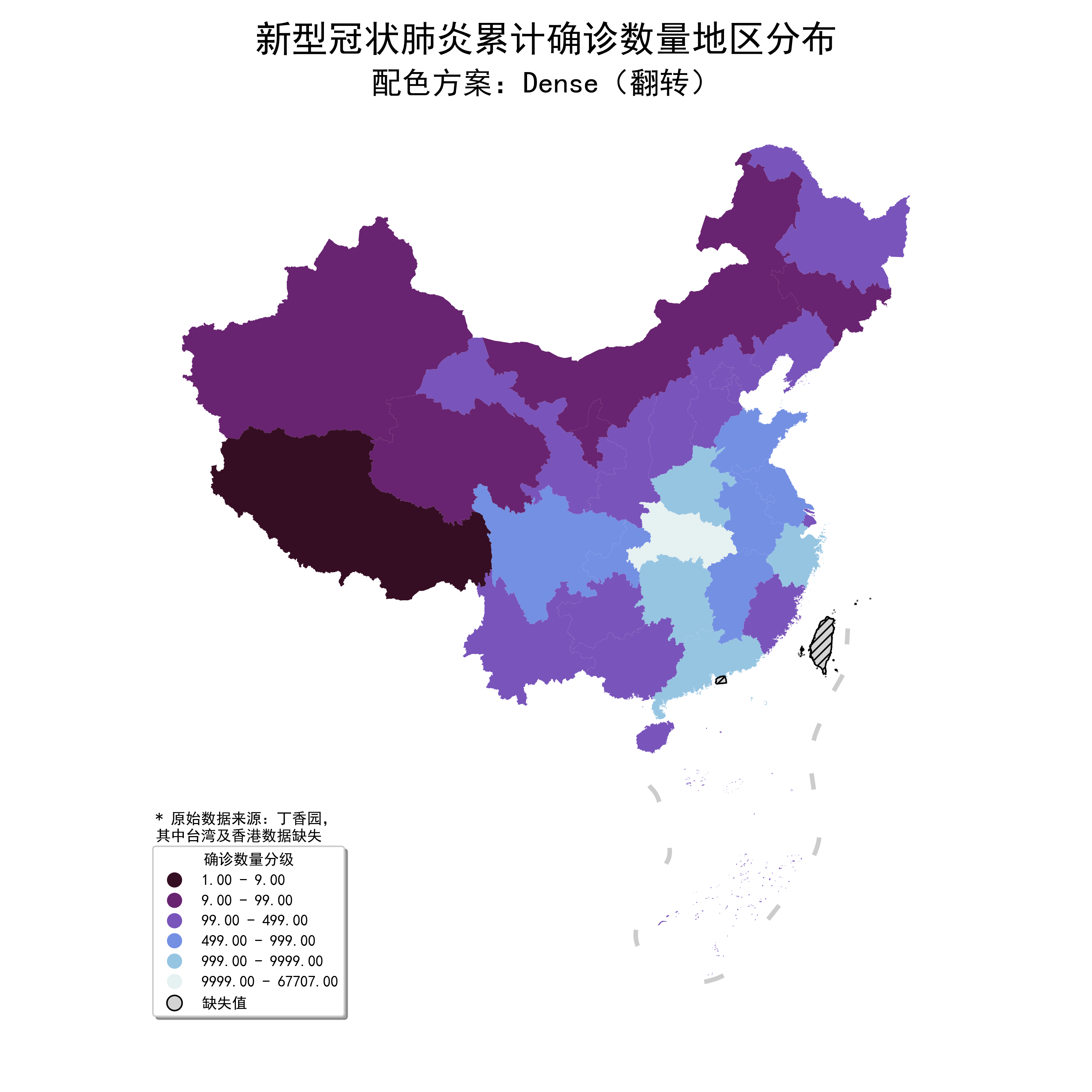
如果想要翻轉映射方向,換成Dense_20_r再重複上述操作即可:
更多palettable自帶色彩方案,可以在https://jiffyclub.github.io/palettable/ 下查看探索。
2.2.2 基於圖片主色的配色
我們在生活中偶然會看到配色方案讓人眼前一亮的海報或畫作,這時如果你想將這些作品中的主要顏色也應用到自己的可視化作品上,可以參考我下面的做法,這裡以我很喜歡的賈樟柯導演的《一直游到海水變藍》中文版海報為例:
思路是抽取所有像素點的RGB三通道值,分別作為三個特徵,輸入k-means中進行聚類,將聚類數量設置為你想要提取出的主色數量:
from sklearn.cluster import KMeans # 構建特徵 rgb = pd.DataFrame([sea[x][y] for x in range(sea.shape[0]) for y in range(sea.shape[1])], columns=['r', 'g', 'b']) # k-means聚類,其中n_clusters表示聚類數量,n_jobs=-1表示開啟所有核心並行運算 model = KMeans(n_clusters=5, n_jobs=-1) model.fit(rgb) # 訓練模型 # 提取聚類簇重心,即我們需要的主色,繪製調色板 plt.bar([i for i in range(model.cluster_centers_.__len__())], height=[1 for i in range(model.cluster_centers_.__len__())], color=[tuple(c) for c in (model.cluster_centers_ / 255.)], width=1) plt.axis('off')

再來個例子,提取《一直游到海水變藍》海外版海報主色:
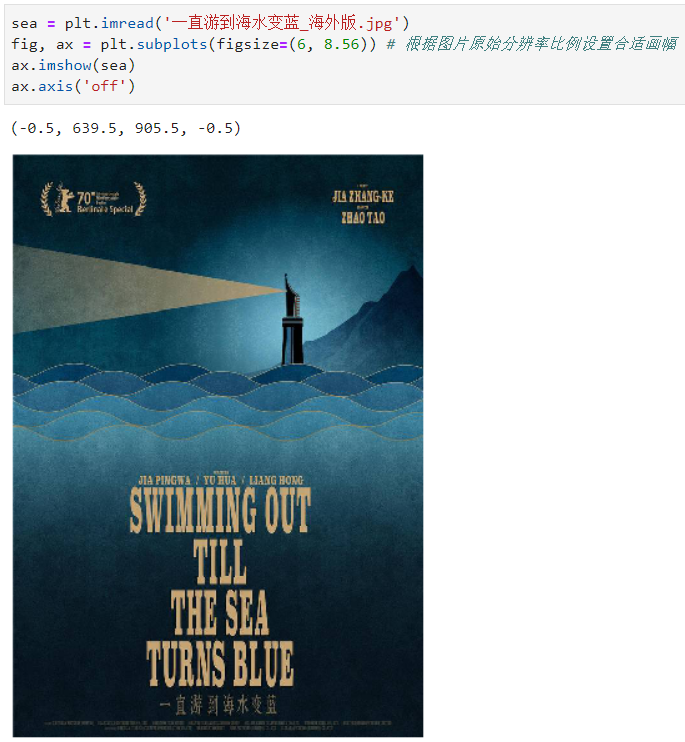
對應提取到的5種主色如圖33:
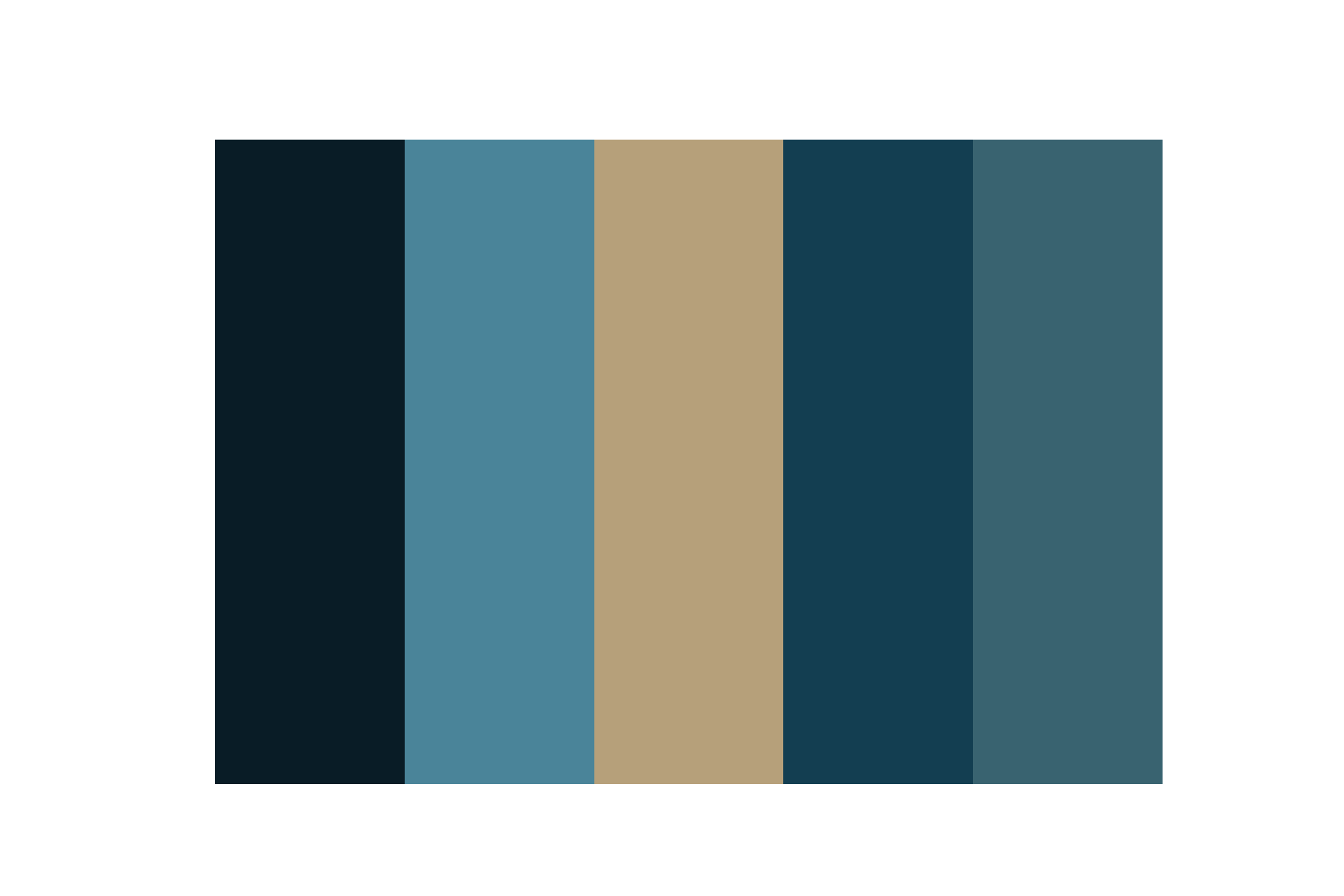
類似的,你可以試著提取你喜愛的平面作品的主色。
以上就是本文的全部內容,如有筆誤望指出。


