影像頻域濾波與傅里葉變換
- 2020 年 3 月 8 日
- 筆記
1、頻率濾波
影像的空間域濾波:用各種模板直接與影像進行卷積運算,實現對影像的處理,這種方法直接對影像空間操作,操作簡單。影像處理不僅可以在空間域進行還可以在頻率域進行,把空間域的影像開窗卷積形式,變換得到頻率域的矩陣點乘形式得到比較好的效果。影像頻域濾波,先把影像轉換到頻域空間,然後對不同的頻率點進行濾波,使用訊號處理的技術,對影像實現濾波。比如實現影像的輪廓提取,在空間域濾波中我們使用一個拉普拉斯模板就可以提取,而在頻域內,我們使用一個高通濾波模板,可以實現輪廓的提取。
影像特徵與像素點數值的關係:
影像尺寸418*564,如果把每一行所有像素,一行564個點的灰度作為一維向量畫圖,取前三行畫成三條曲線,就得到了下面的圖形。
subplot(2,1,1); imshow(img), title('原始影像'); line1 = img(1, :); line2 = img(2, :); line3 = img(3, :); subplot(2,1,2); hold on plot(line1, 'r'); plot(line2, 'g'); plot(line3, 'b');
輸出結果如下圖。
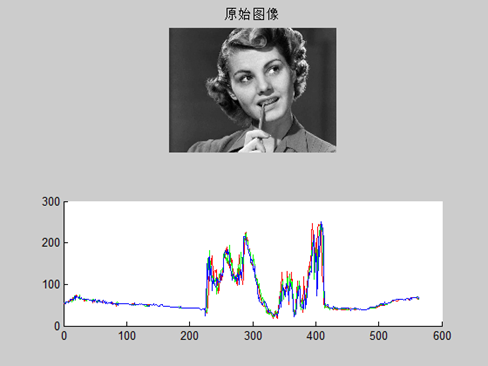
影像前幾行的特徵如下圖(為了方便觀察提取了不止三行):

從影像矩陣前幾行的像素特徵可見,影像平坦的地方像素曲線也平坦,影像亮的地方就是影像像素劇烈變化的地方,影像像素值發生較大差異的地方也是影像發生突變的地方,這些位置一般就是影像輪廓。影像的頻率體現了影像中灰度變化劇烈程度,是灰度在平面空間上的梯度。所以前面講的空域濾波,可以使用平滑來濾除雜訊實現平滑,從上面曲線影像上看,可以按照訊號處理思想來理解,平滑濾波就是頻率低通。對應的,頻率高通濾波就是空域的提取邊界。
2、影像傅里葉變換
傅里葉變換可以將一個時域訊號轉換成在不同頻率下對應的振幅及相位,其頻譜就是時域訊號在頻域下的表現,而反傅里葉變換可以將頻譜再轉換回時域的訊號。
imgPath = 'E:opencv_picsrc_picpic4.bmp'; img = imread(imgPath); img=rgb2gray(img); f=fft2(im2double(img)); %FFT F=f; %FFT頻譜 T=log(F+1); %頻譜對數變換 subplot(1,2,1),imshow(img),title('原始影像'); subplot(1,2,2),imshow(T,[]),title('原始影像其頻譜圖');
輸出結果如下,幅度圖在四個角出現亮光。因為實訊號以fs為取樣速率的訊號在 fs/2處混疊,所以實訊號fft的結果中前半部分對應[0, fs/2],後半部分對應[ -fs/2, 0]。橫向和縱向都需要把頻率轉換到[ -fs/2, fs/2]的區間,可以使用fftshift函數。

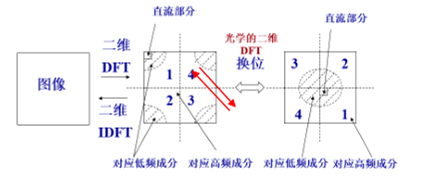
在數字影像處理中,常常需要將F(u,v)的原點移到N*N頻域的中心,以便能清楚地分析傅里葉譜的情況,平移前空域、頻域原點均在左上方。而fftshift的作用就是這樣,將0頻譜移到正中心。
Y = fftshift(X) 通過將零頻分量移動到數組中心,重新排列傅里葉變換 X。
如果 X 是向量,則 fftshift 會將 X 的左右兩半部分進行交換。
如果 X 是矩陣,則 fftshift 會將 X 的第一象限與第三象限交換,將第二象限與第四象限交換。
如果 X 是多維數組,則 fftshift 會沿每個維度交換 X 的半空間。
a = 1 2 3 4 6 7 8 9 >> fftshift(a) ans = 8 9 6 7 3 4 1 2
平移後的圖:

傅里葉變換的能量集中在頻率很小的圓內,當D0增大時能量衰減很快,高頻部分雖然攜帶的能量很少,但是包含豐富的邊界和細節資訊,所以當截止頻率D0變小時,雖然亮度足夠(因能量損失不大),但影像變模糊。

3、頻域濾波
傅里葉變換可以把影像從空域變換到頻域,而傅里葉反變換可以將影像的頻譜變換為空域影像。可以利用影像空域和頻域之間的對應關係,嘗試將空域卷積濾波變換為頻域濾波,而後再將頻域濾波處理後的影像反變換回空間域,從而達到影像增強的目的。
G=imnoise(img,'gaussian', 0, 0.05);%模擬均值為0方差為0.05的高斯雜訊, H=fft2(im2double(G)); %FFT H=fftshift(H); %FFT頻譜平移 T=log(abs(H)); %頻譜對數變換 subplot(2,2,1), imshow(G),title('添加高斯雜訊影像'); subplot(2,2,2),imshow(T, []),title('頻譜圖');

使用傅里葉變換得到影像的頻域幅度,應用傅里葉反變換得到空域影像.
img2 = (ifft2(ifftshift(H))); %===頻域的圖反變換到空域 img3 = im2uint8(mat2gray(img2)); %===取其灰度圖 subplot(2,2,3),imshow(img3); title('anti-Fourier');
反變換效果如下圖。

那麼就可以在頻率對影像進行濾波,然後反變換回空域就得到濾波後的影像。頻率圖可見在影像中心,是頻率為0位置,所以如果限定只有低頻通過則為低通,如果抑制頻譜圖中心位置,則是高通。可見影像在頻域濾波是非常直觀的。
1)低通濾波器:
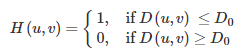
其中D(u,v)為頻率域上(u,v)點到中心的距離,D0由自己設置.

2)高通濾波器:
高通濾波器同低通濾波器非常類似,只不過二者通過的波正好是相反的.
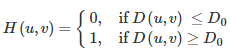

3)高斯低通濾波
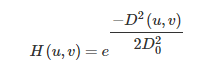

4)高斯高通濾波
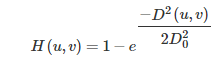
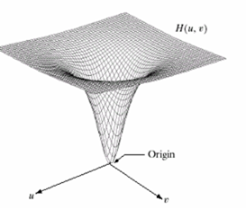
高斯頻率低通濾波:
S=fftshift(fft2(G)); %G是添加高斯雜訊的影像 [M,N]=size(S); n=2; d0=5; %GLPF濾波,d0=5,15,30 n1=floor(M/2); n2=floor(N/2); for i=1:M for j=1:N d=sqrt((i-n1)^2+(j-n2)^2); h=1*exp(-1/2*(d^2/d0^2)); S(i,j)=h*S(i,j); end end S=ifftshift(S); S=uint8(ifft2(S)); subplot(2,2,4),imshow(S),title('高斯低通濾波影像');
輸出影像如下:

高斯濾波函數標準差變大,則高斯函數的傅里葉變換影像頻率範圍變寬,允許通過的頻率範圍變大,對應空域允許通過的影像變換更加多,可以允許的雜訊更多。相反,如果標準差變小,頻域範圍變窄,允許通過的頻率範圍變小,對應空域對低頻要求更加嚴格被抑制的高頻更多,所以影像更加平滑,可能出現模糊現象。下面展示了不同的σ標準差情況下的濾波效果。

改為高通濾波,結果如下圖:

5、參考文獻:
1、《數字影像處理與機器視覺》
第二版。 張錚、徐超、任淑霞、韓海玲等編著。
2、傅里葉變換在影像處理中的應用
https://www.cnblogs.com/Lynn0101/p/9892469.html
3、fftshift
https://ww2.mathworks.cn/help/matlab/ref/fftshift.html


