數據結構與演算法系列十(排序演算法概述)
- 2020 年 3 月 8 日
- 筆記
有人說,數據結構與演算法,電腦網路,與作業系統都一樣,脫離日常開發,除了面試這輩子可能都用不到呀!
有人說,我是做業務開發的,只要熟練API,熟練框架,熟練各種中間件,寫的程式碼不也能“飛”起來嗎?
於是問題來了:為什麼還要學習數據結構與演算法呢?
#理由一: 面試的時候,千萬不要被數據結構與演算法拖了後腿 #理由二: 你真的願意做一輩子CRUD Boy嗎 #理由三: 不想寫出開源框架,中間件的工程師,不是好廚子
我想好了,還是需要學習數據結構與演算法。但是我有兩個困惑:
1.如何著手學習呢?
2.有哪些內容要學習呢?
學習方法推薦:
#學習方法 1.從基礎開始,系統化學習 2.多動手,每一種數據結構與演算法,都自己用程式碼實現出來 3.思路更重要:理解實現思想,不要背程式碼 4.與日常開發結合,對應應用場景
學習內容推薦:
數據結構與演算法內容比較多,我們本著實用原則,學習經典的、常用的數據結構、與常用演算法
#學習內容: 1.數據結構的定義 2.演算法的定義 3.複雜度分析 4.常用數據結構 數組、鏈表、棧、隊列 散列表、二叉樹、堆 跳錶、圖 5.常用演算法 遞歸、排序、二分查找 搜索、哈希、貪心、分治 動態規劃、字元串匹配
在前面兩篇,我們詳細看了常用演算法的第一個主題:遞歸。接下來我們來看常用演算法的第二個主題:排序。排序內容有點多,常見的排序演算法就有:冒泡排序、插入排序、選擇排序、歸併排序、快速排序、桶排序、計數排序、基數排序。
這些排序演算法中,不知道有沒有你熟悉的,或者不熟悉的。讓我們開啟排序演算法之旅吧。首先第一篇中,我們先來對排序演算法做一個總體上的認識。
#考考你: 1.你知道常用的排序演算法有哪些嗎? 2.你知道如何衡量排序演算法的優劣嗎? 3.你知道排序演算法的基礎概念:有序度、逆序度、滿有序度嗎?
在考考你中,我們說排序演算法有:冒泡排序、插入排序、選擇排序、歸併排序、快速排序、桶排序、計數排序、基數排序。這樣看起來有點散亂,能不能給它們歸一下類呢?答案是可以的。
對於排序演算法,我們可以從時間複雜度上進行歸類:
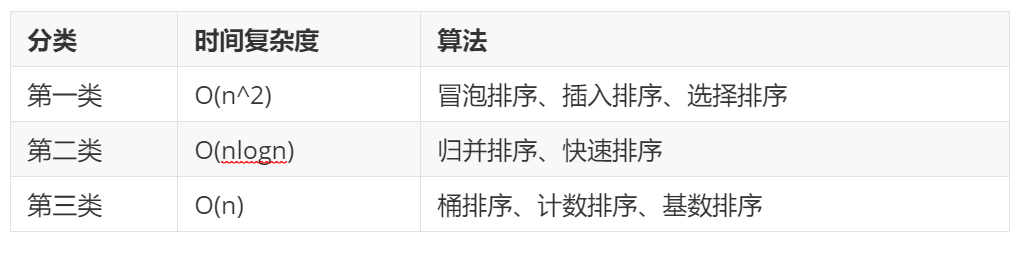
在實際軟體開發中,有眾多的排序演算法,如何選擇和取捨呢?真的會有選擇困難症啊!有沒有一些好的、可行的方法,去綜合衡量排序演算法的優劣呢?
答案是:有
我們可以從三個角度去綜合分析排序演算法:時間複雜度、空間複雜度、演算法穩定性
#時間複雜度 1.分析最好情況、最壞情況、平均情況時間複雜度 2.複雜度分析中,關於係數、常數、低階平常可以省略 3.但是,需要特別注意:在排序演算法中,我們需要考慮進來 #空間複雜度 1.空間複雜度分析,主要看是否是:原地排序演算法 2.原地排序演算法,是指:空間複雜度是O(1) 3.注意:在實際軟體開發中,這一條很重要 #演算法穩定性 1.演算法穩定性,是指如果待排序序列中,有值相同的元素 2.如果經過排序後,原來值相同的元素,順序保持不變 3.那麼我們說,該排序演算法是穩定的排序演算法 4.否則,該排序演算法是不穩定排序演算法 5.比如,有一個待排序序列:3,6,5,2,6,8 6.待排序序列中,有兩個值為6的元素 7.假設用數組a來存儲,對應的下標是:a[1]=6,a[4]=6 8.排序後:a[3]=6,a[4]=6 9.這裡的a[3]是排序前的a[1] 10.這裡的a[4]還是排序前的a[4] 11.這就是穩定排序演算法的要求,如下圖:
理解排序演算法穩定性:

在排序演算法中,我們需要關注三個基礎概念:有序度、逆序度、滿有序度。
整個排序過程,我們可以理解為:增加有序度,減少逆序度,最終達到滿有序度的過程。
那麼,它們具體的含義是什麼呢?
#有序度: 待排序序列中,如果下標索引:i<j,且a[i]<a[j],則稱為有序度 #逆序度 待排序序列中,如果下標索引:i<j,且a[i]>a[j],則稱為逆序度 #滿有序度 1.待排序序列中,如果有序度達到:n(n-1)/2,則稱為滿有序度 2.即此時待排序序列,其實是有序的
以上關於有序度、逆序度的概念,相信很多朋友都能理解。這裡我們解釋一下關於滿有序度的公式:n(n-1)/2。
要理解滿有序度的概念,你可能需要回顧一下數學中的:排列、組合知識點,應該是在高二的時候學的,可以這樣去理解它們:
#排列: 1.有n個元素,如果每兩個元素,組成一個排列 2.則總共有排列數:n(n-1) 3.比如,有3個元素:a b c 4.每兩個元素組成排列數是:3*(3-1)=6 5.組成的排列有:(a,b) (a,c) (b,a) (b,c) (c,a) (c,b) #組合: 1.有n個元素,如果每兩個元素,組成一個組合 2.則總共有組合數:n(n-1)/2 3.比如,有3個元素:a b c 4.每兩個元素組成的組合數是:3(3-1)/2=3 5.組成的組合有:(a,b) (a,c) (b,c) #綜合結論: 1.假設待排序序列有n個元素 2.如果有序度,等於每2個元素的組合數:n(n-1)/2 3.那麼該待排序序列,其實是有序的 4.這就是滿有序度的概念

