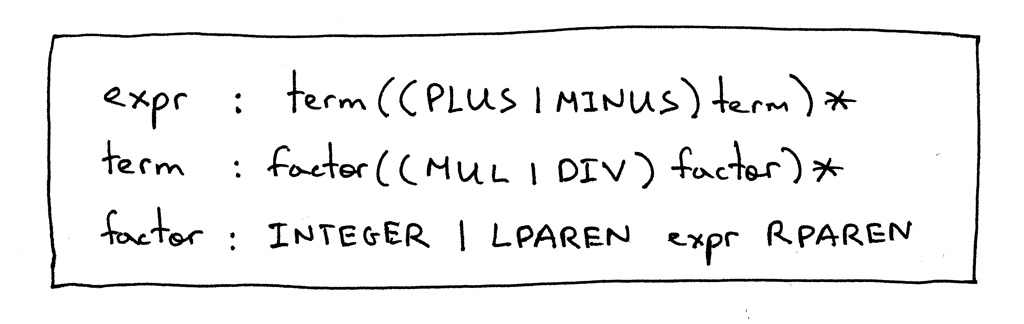
矢量線的一種柵格化演算法
- 2020 年 3 月 4 日
- 筆記
1. 概述
1.1. 已知演算法
將一條線段柵格化的最簡單的演算法思路是根據其斜率,按X或Y方向步進取值:
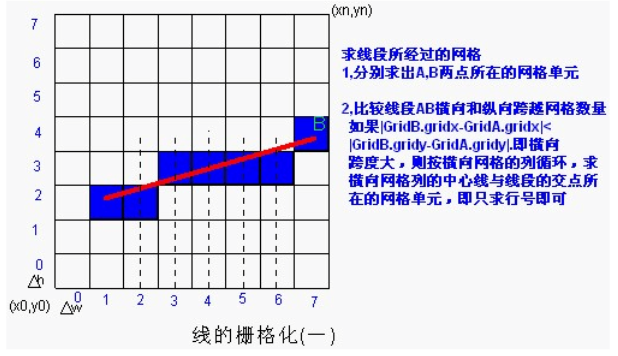
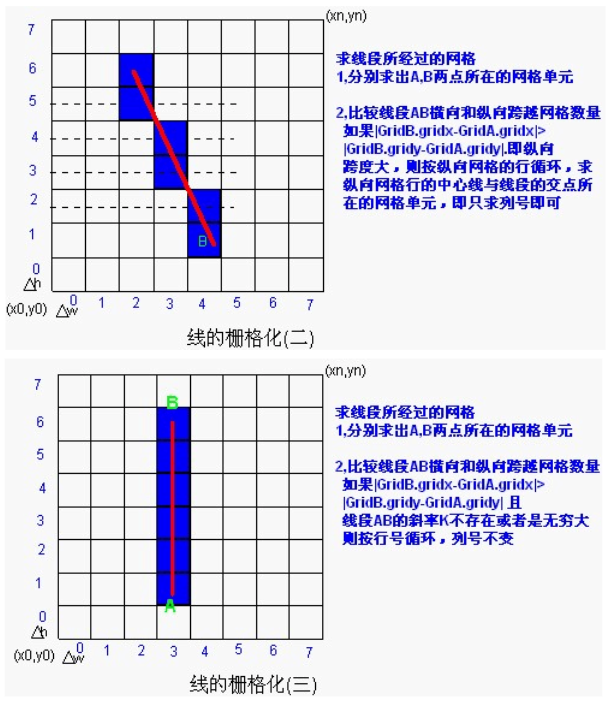
除此之外還有一種演算法是利用電腦圖形學中繪製直線的Bresenham演算法,這種演算法的效率很高,原理就是用遍歷的辦法規避乘法和除法,只用加減法就能完成線段的柵格化。
1.2. 本文演算法
上述兩種演算法有個問題就是都要經過一系列繁複的判斷,才能得到比較嚴密的結果,所以我並沒有採用。我這裡採用的演算法也是逐漸步進求值的辦法,只不過不再沿著X或者Y方向求值,而是沿著射線方向步進。這裡的射線指的是從線段的起點開始,以1像素為步進單位,步進到線段的終點。因為線段的方向性問題,步進得到的點總會有重複的值,最後再進行去重操作即可。
演算法過程簡述如下:
- 設線段的起點為(O),終點為(E),則方向向量為(D=E-O);
- 線段的長度L為向量(D)的模。以0為初值,L為終值,以1為步進值建立一個for循環,每次取的長度為d;
- 令(t=d/L),則線段上相應的點為(P=O+tD)。這個公式是根據射線向量方程推導出來的,可以參看這篇文章《已知線段上某點與起點的距離,求該點的坐標》;
- 將取的點都保存到容器中;
- 對容器中的點進行去重操作。
最終得到的點即為直線柵格化後的點。
2. 實現
具體的C++實現程式碼如下:
#include <iostream> #include <vector> using namespace std; const double EPSILON = 0.000001; // 2D Point struct Vector2d { public: Vector2d() { } Vector2d(double dx, double dy) { x = dx; y = dy; } // 矢量賦值 void set(double dx, double dy) { x = dx; y = dy; } // 矢量相加 Vector2d operator + (const Vector2d& v) const { return Vector2d(x + v.x, y + v.y); } // 矢量相減 Vector2d operator - (const Vector2d& v) const { return Vector2d(x - v.x, y - v.y); } //矢量數乘 Vector2d Scalar(double c) const { return Vector2d(c*x, c*y); } // 矢量點積 double Dot(const Vector2d& v) const { return x * v.x + y * v.y; } //向量的模 double Mod() const { return sqrt(x * x + y * y); } bool Equel(const Vector2d& v) const { if (abs(x - v.x) < EPSILON && abs(y - v.y) < EPSILON) { return true; } return false; } double x, y; }; //柵格化一條線段 void RasterLine(std::pair<Vector2d, Vector2d> line, std::vector<Vector2d>& linePointList) { Vector2d vecLine = line.second - line.first; double lineLength = vecLine.Mod(); double step = 1.0; //根據距離逐步取 vector<Vector2d> tmpPointList; double curLength = 0; while (curLength < lineLength) { curLength = curLength + step; Vector2d P = line.first + vecLine.Scalar(curLength / lineLength); P.x = (int)(P.x + 0.5); P.y = (int)(P.y + 0.5); tmpPointList.push_back(P); } //與最後一個值比較,去重 linePointList.push_back(line.first); for (size_t i = 0; i < tmpPointList.size(); i++) { //與最後一個值比較,去重 if (!tmpPointList[i].Equel(linePointList[linePointList.size() - 1])) { linePointList.push_back(tmpPointList[i]); } } if (!linePointList[linePointList.size() - 1].Equel(line.second)) { linePointList.push_back(line.second); } } int main() { Vector2d O(30, 60); Vector2d E(88, 104); std::pair<Vector2d, Vector2d> line(O, E); vector<Vector2d> linePointList; RasterLine(line, linePointList); for (size_t i = 0; i < linePointList.size(); i++) { cout << linePointList[i].x << ',' << linePointList[i].y << 't'; } }其運行的結果如下:

3. 參考
[1].矢量數據柵格化
[2].Bresenham演算法