《Deep Learning of Graph Matching》論文閱讀
- 2020 年 3 月 4 日
- 筆記
1. 論文概述
論文首次將深度學習同圖匹配（Graph matching）結合，設計了end-to-end網路去學習圖匹配過程。
1.1 網路學習的目標（輸出）
是兩個圖（Graph）之間的相似度矩陣。
1.2 網路的輸入
拿其中的 imageNet 的鳥舉例如下圖，使用的是另一篇論文使用的數據集。數據特點：①鳥的姿態幾乎一致②每個鳥選取15個關鍵點。這樣就默認不同二圖中相對應的點（如下圖不同顏色的點）是 一 一 匹配的，即當作ground-truth。具體如何將image輸入得到graph，下文講。
1.3 論文的loss設計
由1.2節我們知道了ground-truth，所以loss的設計：因為我們已經知道二圖目標點的相互匹配結果，所以對於網路訓練得到的匹配結果，我們使用網路輸出的結果和真實匹配點之間的物理位移作為考量因素。具體見下文。
2. 網路設計
2.1 網路基本結構
按順序大概介紹每層功能：
第一層（預處理）：將上文提到的數據集（比如鳥：①姿態一致②兩圖15個關鍵點）通過vgg16提取特徵。一階特徵代表點的特徵資訊，二階特徵代表邊的特徵資訊，分別使用淺層的relu4_2激活資訊和relu5_1的激活資訊，分別記作F和U，下圖的U，F的上標表示兩個圖。輸入二圖，輸出F，U
第二層：通過輸入的F，U構建二圖的相似度矩陣。輸入上一層的F，U，輸出相似度矩陣M
第三層：輸入M，輸出v*。主要求解相似度矩陣的最大特徵向量，當作近似的圖匹配的解
第四層：輸入v*，輸出排列陣S。主要將排列陣按行、列 歸一化，歸一化成雙隨機矩陣
第五層：對排列陣S，按概率選擇每一個點對應的匹配結果
第六層：求loss，並反向傳播
3. Deep Feature Extractor層
使用VGG16提取點、邊的特徵資訊，輸入到下一層。分別記作F、U，上標表示二圖
4. Affinity Matrix Factorization
介紹下論文使用的相似度矩陣，使用分解形式如下：
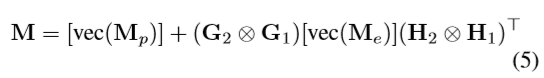
二圖的邊和點結點分別為：n點p邊。m點q邊。[..]是將向量變成diagonal矩陣。vec()是將矩陣按列（有些論文是按行）
第一項[vec(Mp)]是正則項。
看下圖，H1,G1分別代表圖一的點和邊結點的表示，H2、G2類似。
Me表示邊結點相似度，X、Y的構成不包含運算，個人認為是輸入的F、U的拼接。其中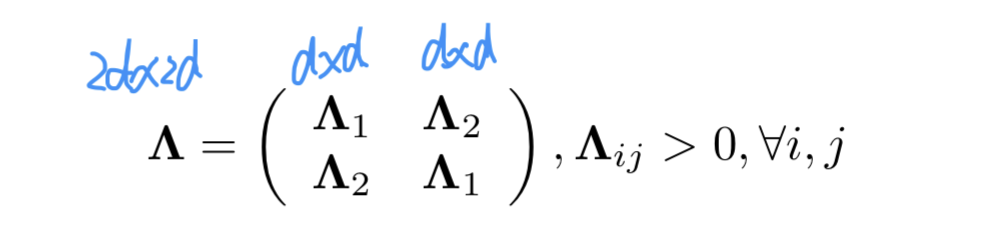 
是要訓練的對象
5. 矩陣符號
其中 “：”表示矩陣的內積（對應元素相乘）。（4）式表示函數的偏導數
6. Affinity matrix layer
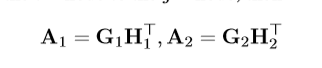
該層的後向傳播分析：因為上一層傳入的變數是FU，參數存儲在 “半三角形”這個符號中，所以需要求出對FU的偏導，更具上一節，即等於求出X Y的偏導。
中間的為推導需要使用的公式。
7. Power Iteration Layer
因為圖匹配數學模型為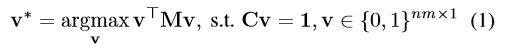
，其中M為上文的相似度矩陣，為了使上式最大化，可使用M的最大特徵向量來近似，所以這層先使用冪迭代方法，求出M的最大特徵向量。（通過閉式解方法）
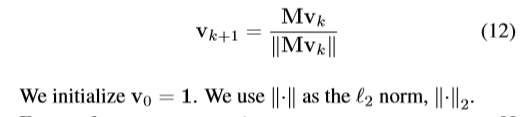
該層反向傳播：
推導中紅線第一個等式：
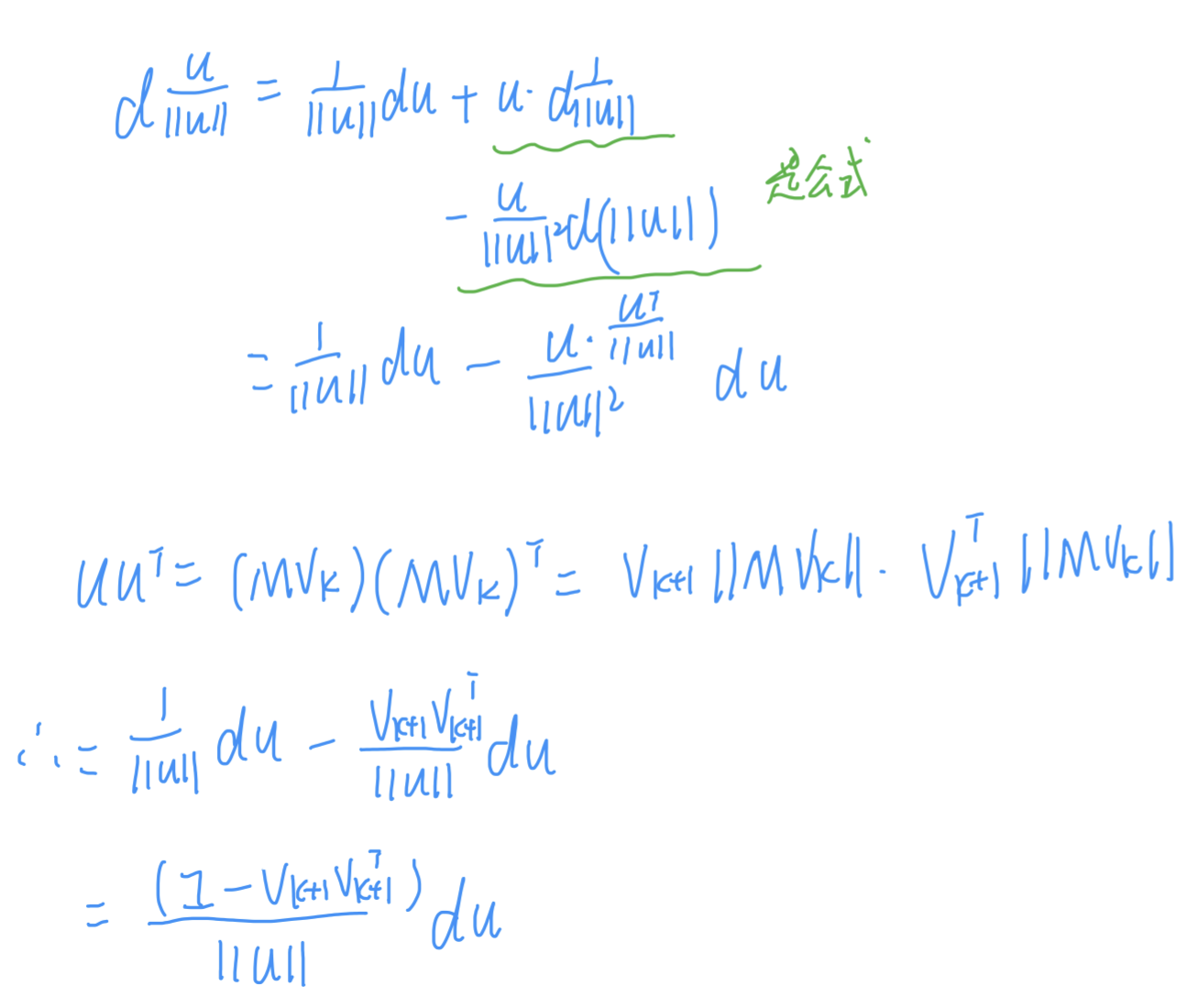
所以結果：
為了進一步降低計算複雜度：
最終結果：
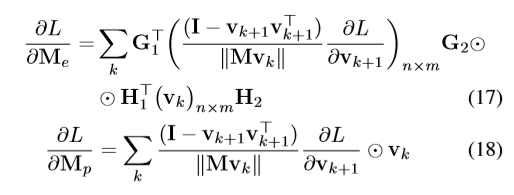
8. bi-stochasic layer
這層就是將上一層輸入的vk向量變成雙隨機矩陣。分別進行行、列的歸一化。
那麼進一步推導反向傳播：
9. voting 和 loss
輸入時上一層的s雙隨機矩陣，所以只要選出概率最大的點就代表這兩個點互相匹配，這裡的loss函數就是計算匹配的點和真實點的物理位置。
設計基本按照softmax而來。但是我有疑問，就是為什麼要減去Pi，感覺不用減，在(23)式中不是在減了嘛？
其中P式m*2維數，所以應該是第二張圖的個點的物理位置。
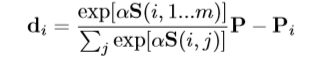
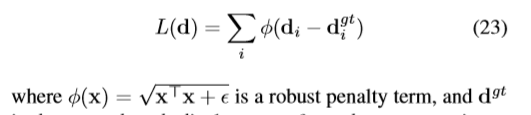
有做圖匹配的同學歡迎交流！！
論文原文：Deep Learning of Graph Matching
參考：https://zhuanlan.zhihu.com/p/54034817
