一個動態規劃的簡單例題
動態規劃(Dynamic Programming)
它是電腦中解決最優化問題的一種方法,效率高,速度快。
一般思路:
- 1、窮舉法/暴力搜索
- 2、記憶化搜索/剪枝
- 3、改寫成迭代形式
思想
1.動態規劃演算法與分治法類似,其基本思想也是將待求解問題分解成若干個子問題
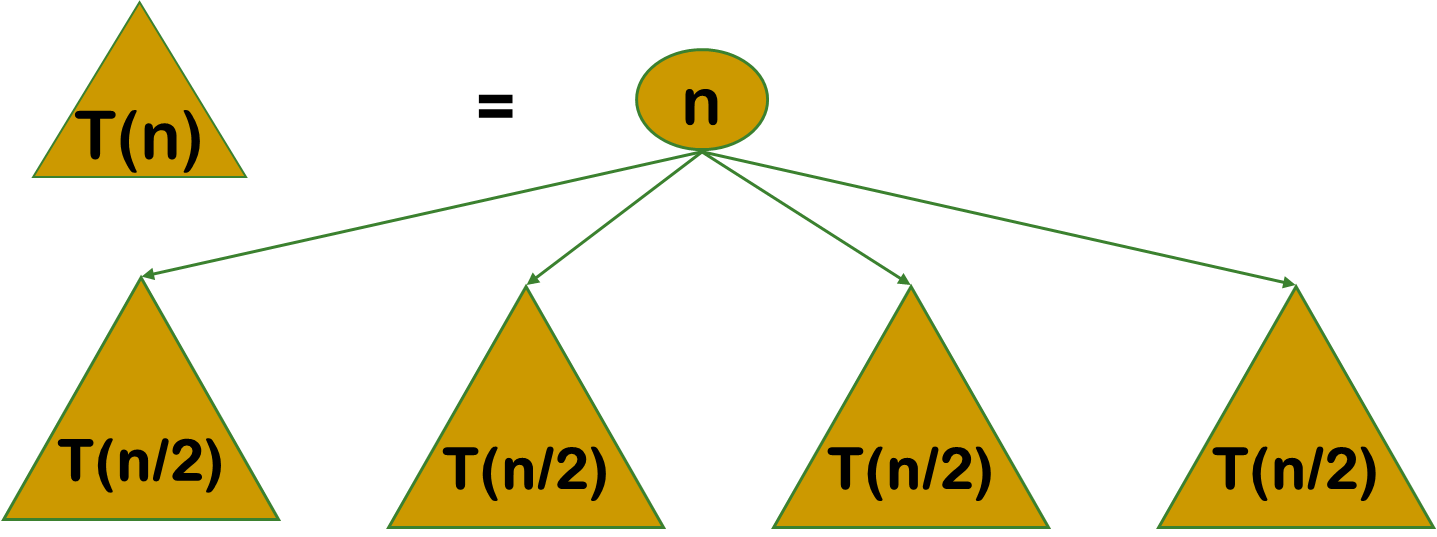
2.但是經分解得到的子問題往往不是互相獨立的。不同子問題的數目常常只有多項式量級。在用分治法求解時,有些子問題被重複計算了許多次。
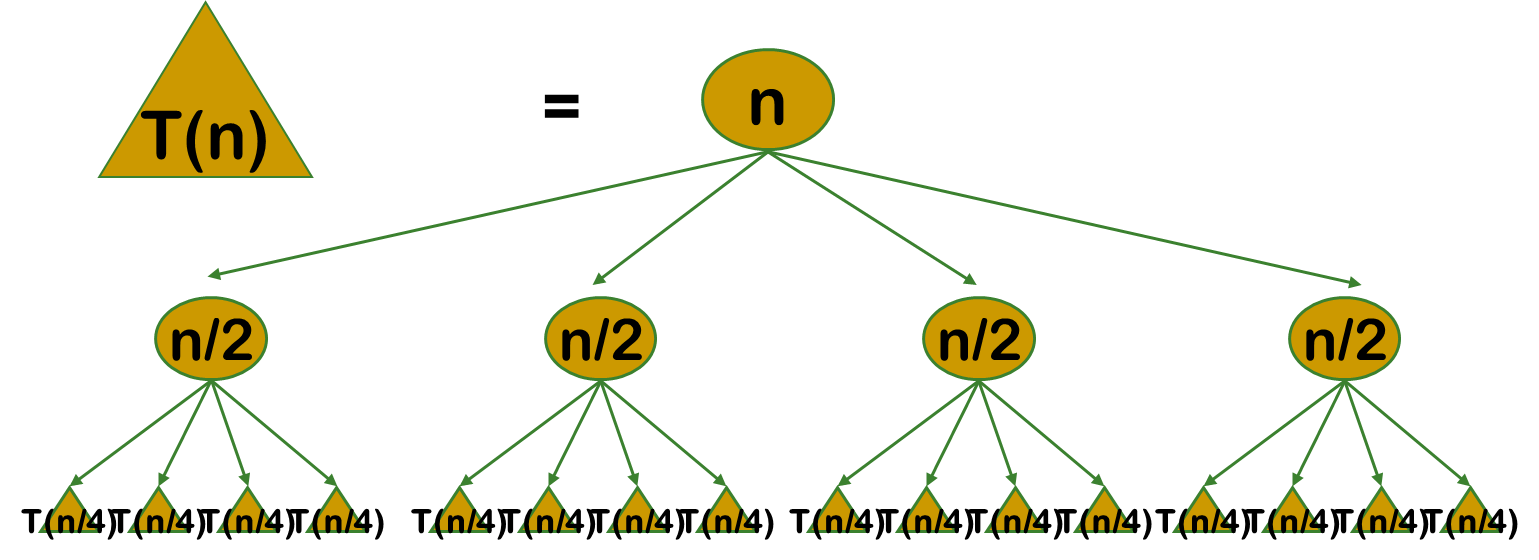
3.如果能夠保存已解決的子問題的答案,而在需要時再找出已求得的答案,就可以避免大量重複計算,從而得到多項式時間演算法。
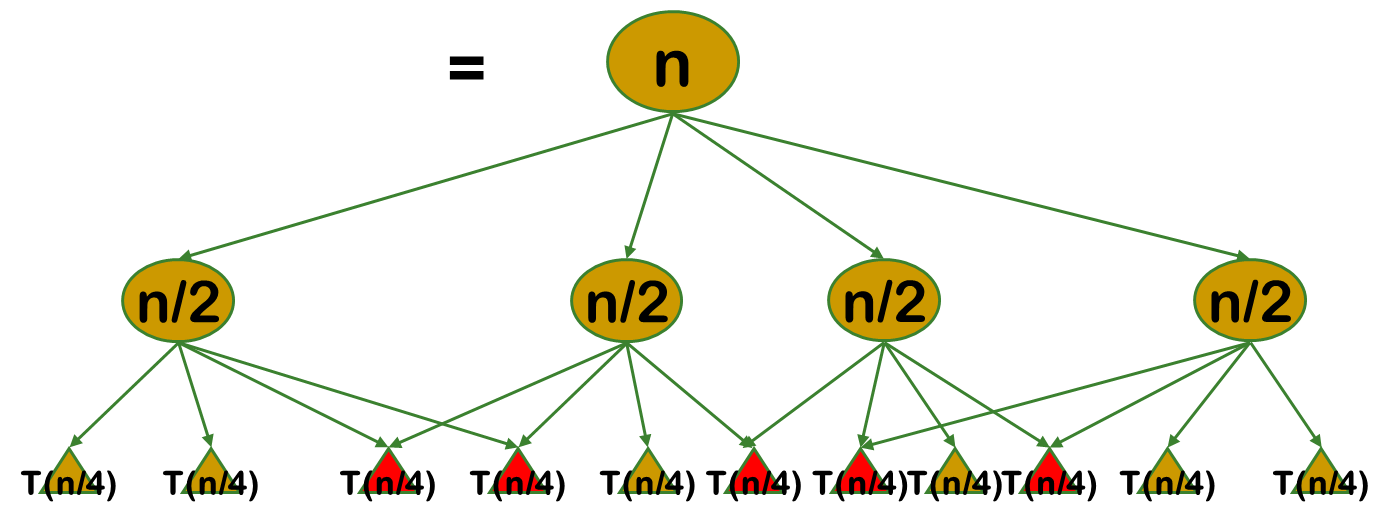
例題
e.g
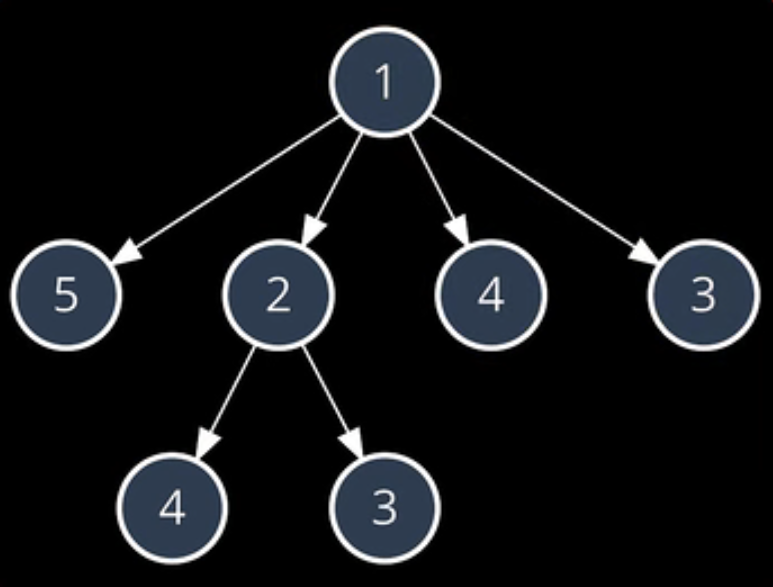
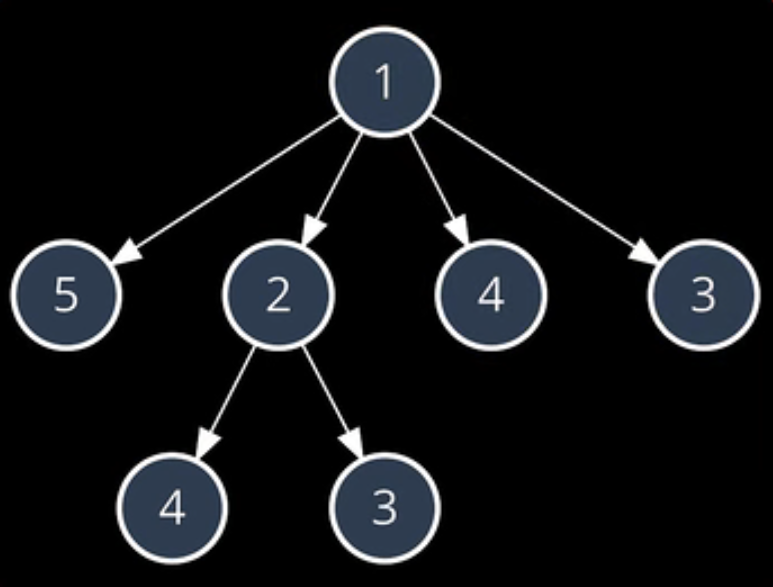
找出最長的遞增的子序列 ,nums = [1,5,2,4,3]
給了一個無序的數組,要求我們找出其中最長的遞增的子序列,比如:1,2,4就是其中的一個;1,2,3是另外一個。
我們可以將問題簡化:要求這個演算法只返回最長序列的「長度」
利用暴力枚舉/暴力搜索:從「1」出發,最長遞增子序列長度:3
演算法實現:
def L( nums , i ):# 我們可以定義一個函數L,這個函數會返回從數組第i個數字開始的最長子序列長度
if i == len(nums) - 1 : # 取到最後一個數字
return 1
for j in range ( i + 1 ,len( nums ) ) : # 檢查i後面的所有數字,將索引記為j
#遍歷所有的j
if nums [ j ] > nums [ i ] : # 只要這個數比當前數大(也就是說可以構成遞增序列)
max_len = max( max_len , L( nums , j ) + 1) # 遞歸的調用函數自身,去計算從j開始的最長子序列長度,然後+1得到目前這個序列的總長度
return max_len
# 接下來只需要對數組中的每一個數i ,依次調用L函數,然後選出長度最長的那個返回即可
def length_of_LTS(nums):
return max(
L(nums , i )for i in range ( len( nums))
)
# 可以帶入之前的數據進行測試
nums = [1,5,2,4,3]
print(length_of_LTS(nums))
演算法優化:記憶化搜索
再次觀察下方的遍歷樹,我們遍歷子序列1,2,4的時候就已經計算過”從4開始的最大子序列的長度”,後面遍歷1,4的時候又計算了一次。因此演算法存在大量重複的計算。
解決方案的關鍵是我們可以在第一次計算的時候,將結果保留下來。
def L( nums , i ):
if i in memo:# 看開頭是否保存過這個答案
return memo [ i ]# 如果是,直接返回結果
# 否則再去計算答案
if i == len(nums) - 1: # 取到最後一個數字
return 1
for j in range ( i + 1 ,len( nums ) ) :
if nums [ j ] > nums [ i ]:
max_len = max( max_len , L( nums , j ) + 1) # 遍歷所有的j
memo[ i ] = max_len # 哈希表,記錄下「從i開始最長的子序列長度」
return max_len
def length_of_LTS(nums):
return max(
L(nums , i )for i in range ( len( nums))
)
這裡用到了記憶化搜索,這也就是為什麼大家常說用空間換時間
迭代/非遞歸的實現
從最後的式子可以推至開頭的式子,是不是很像數學歸納法?
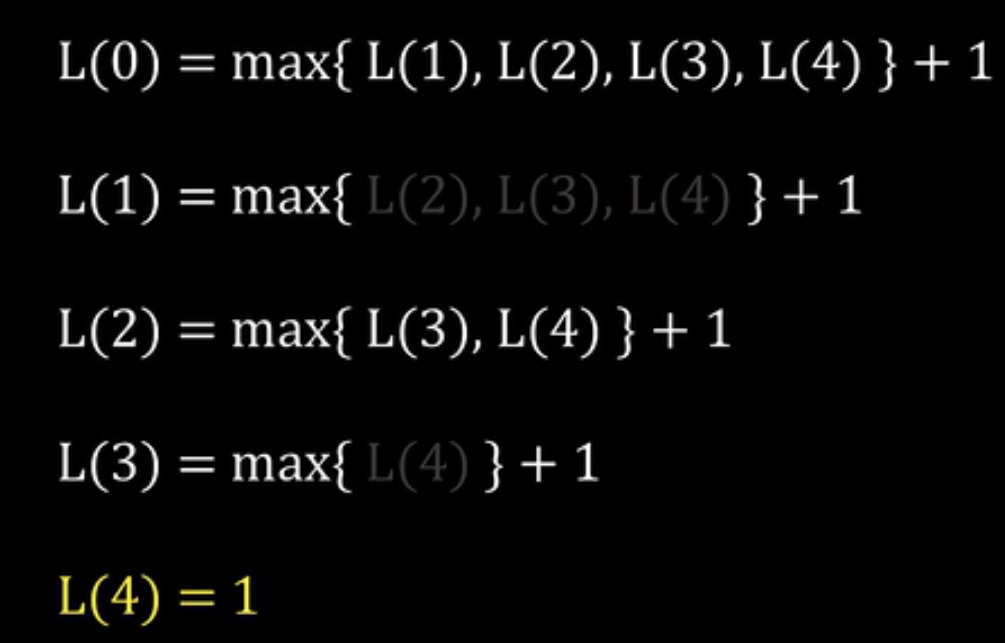
def length_of_LTS(nums);
n = len( nums ) # 5
L = [1 ] * n # initial value: [1,1,1,1,1]
# 通過兩個循環,外面的循環代表從下往上的依次計算;裡面的循環用於遍歷括弧中的這些數值,運算的結果可以存放到一個數組中,直接叫L
for i in reversed(range(n)): # i -> 4,3,2,1,0
for j in range(i + 1 , n):
if nums [ j ] > nums [ i ] :
L[ i ] = max(L[ i ],L [ j ] + 1)
return max(L)
10分鐘徹底搞懂「動態規劃」演算法_嗶哩嗶哩_bilibili
配套影片的鏈接哦


