第二次部落格作業
- 2022 年 10 月 29 日
- 筆記
目錄
前言
設計與分析
采坑心得
改進建議
總結
(1)前言:總結之前所涉及到的知識點、題量、難度等情況
期中考試的難度是逐漸提高的,但是因為給了類圖,難度總的來說比較適中。
第四次的pta作業中第一題和第三題難度比較簡單,第二題的難度挺高的,很考驗編程能力和對正則表達式的使用。
第五次的pta作業難度是最高的一次作業。
(2)設計與分析:重點對題目的提交源碼進行分析,可參考SourceMonitor的生成報表內容以及PowerDesigner的相應類圖,要有相應的解釋和心得(做到有圖有真相),本次Blog必須分析PTA中的圖形類設計的題目、超星中鏈表類練習題目以及期中考試的三道題目
用戶輸入一組選項和數據,進行與四邊形有關的計算。
以下四邊形頂點的坐標要求按順序依次輸入,連續輸入的兩個頂點是相鄰頂點,第一個和最後一個輸入的頂點相鄰。
選項包括:
1:輸入四個點坐標,判斷是否是四邊形、平行四邊形,判斷結果輸出true/false,結果之間以一個英文空格符分隔。
2:輸入四個點坐標,判斷是否是菱形、矩形、正方形,判斷結果輸出true/false,結果之間以一個英文空格符分隔。 若四個點坐標無法構成四邊形,輸出”not a quadrilateral”
3:輸入四個點坐標,判斷是凹四邊形(false)還是凸四邊形(true),輸出四邊形周長、面積,結果之間以一個英文空格符分隔。 若四個點坐標無法構成四邊形,輸出”not a quadrilateral”
4:輸入六個點坐標,前兩個點構成一條直線,後四個點構成一個四邊形或三角形,輸出直線與四邊形(也可能是三角形)相交的交點數量。如果交點有兩個,再按面積從小到大輸出四邊形(或三角形)被直線分割成兩部分的面積(不換行)。若直線與四邊形或三角形的一條邊線重合,輸出”The line is coincide with one of the lines”。若後四個點不符合四邊形或三角形的輸入,輸出”not a quadrilateral or triangle”。
後四個點構成三角形的情況:假設三角形一條邊上兩個端點分別是x、y,邊線中間有一點z,另一頂點s:
1)符合要求的輸入:頂點重複或者z與xy都相鄰,如x x y s、x z y s、x y x s、s x y y。此時去除冗餘點,保留一個x、一個y。
2) 不符合要求的輸入:z 不與xy都相鄰,如z x y s、x z s y、x s z y
5:輸入五個點坐標,輸出第一個是否在後四個點所構成的四邊形(限定為凸四邊形,不考慮凹四邊形)或三角形(判定方法見選項4)的內部(若是四邊形輸出in the quadrilateral/outof the quadrilateral,若是三角形輸出in the triangle/outof the triangle)。如果點在多邊形的某條邊上,輸出”on the triangle或者on the quadrilateral”。若後四個點不符合四邊形或三角形,輸出”not a quadrilateral or triangle”。
輸入格式:
基本格式:選項+”:”+坐標x+”,”+坐標y+” “+坐標x+”,”+坐標y。點的x、y坐標之間以英文”,”分隔,點與點之間以一個英文空格分隔。
輸出格式:
基本輸出格式見每種選項的描述。
異常情況輸出:
如果不符合基本格式,輸出”Wrong Format”。
如果符合基本格式,但輸入點的數量不符合要求,輸出”wrong number of points”。
注意:輸出的數據若小數點後超過3位,只保留小數點後3位,多餘部分採用四捨五入規則進到最低位。小數點後若不足3位,按原始位數顯示,不必補齊。例如:1/3的結果按格式輸出為 0.333,1.0按格式輸出為1.0
選項1、2、3中,若四邊形四個點中有重合點,輸出”points coincide”。
選項4中,若前兩個輸入線的點重合,輸出”points coincide”。
輸入樣例1:
選項1,點重合。例如:
1:-1,-1 -1,-1 1,2 1,-2輸出樣例:
在這裡給出相應的輸出。例如:
points coincide輸入樣例2:
不符合基本格式。例如:
1:-1,-1 1,2 -1,1 ++1,0輸出樣例:
在這裡給出相應的輸出。例如:
Wrong Format輸入樣例3:
選項1,輸入點數量不對。例如:
1:-1,-1 -1,2 輸出樣例:
在這裡給出相應的輸出。例如:
wrong number of points輸入樣例4:
選項1,正確輸入判斷。例如:
1:-1,-1 -1,1 1,2 1,-2輸出樣例:
在這裡給出相應的輸出。例如:
true false輸入樣例5:
選項2,輸入點不構成四邊形。例如:
2:10,10 1,1 0,0 1,20輸出樣例:
在這裡給出相應的輸出。例如:
not a quadrilateral輸入樣例6:
選項2,正方形。例如:
2:0,0 0,80 80,80 80,0輸出樣例:
在這裡給出相應的輸出。例如:
true true true輸入樣例7:
選項2。例如:
2:0,0 -10,80 0,160 -10,80輸出樣例:
在這裡給出相應的輸出。例如:
not a quadrilateral輸入樣例8:
選項3,凸四邊形。例如:
3:-1,-1 -1,1 1,2 1,-2輸出樣例:
在這裡給出相應的輸出。例如:
true 10.472 6.0輸入樣例9:
選項3,。例如:
3:0,0 -10,100 0,99 10,100輸出樣例:
在這裡給出相應的輸出。例如:
false 221.097 990.0
其餘樣例,詳見附件:
類圖:

程式碼軟體分析:

程式碼主要類:
class Judge { ArrayList<Point> pt = new ArrayList<>(); private int number; public int getIndex() { return number; } public void judge(String s) { int flag =0; String regex = "[1-5]:([+-]?(0|(0\\.[0-9]+)|([1-9][0-9]*(\\.[0-9]+)?)),[+-]?(0|(0\\.[0-9]+)|([1-9][0-9]*(\\.[0-9]+)?))\\s?)+$"; if(s.matches(regex)) { String[] string01 = s.split(":"); number = Integer.parseInt(string01[0]); String[] strings = string01[1].split(" "); for (int i = 0; i < strings.length; i++) { Point pot = new Point(); String[] s1 = strings[i].split(","); pot.setX(Double.parseDouble(s1[0])); pot.setY(Double.parseDouble(s1[1])); pt.add(pot); } } else { System.out.println("Wrong Format"); System.exit(0); } } public boolean number(){ if((pt.size() == 4 && (this.number >= 1 && this.number < 4 )) || (pt.size() == 6 && this.number == 4 ) || (pt.size() == 5 && this.number == 5)) { return true; } else return false; } //判斷點是否重合 public boolean coincidence(ArrayList<Point> a) { for (int i = 0; i < a.size(); i+=2) { for (int j = i+1; j < a.size(); j++) { if(a.get(i).getX() == a.get(j).getX() && a.get(i).getY() == a.get(j).getY()) { System.out.println("points coincide"); return false; } } } return true; } //去冗餘 public void coincidence2() { if(pt.get(0).chonghe(pt.get(2))) pt.remove(0); else if(pt.get(1).chonghe( pt.get(3))) pt.remove(1); //判斷重複的點 for (int i = 0; i < pt.size() - 1; i++) { if(pt.get(i).chonghe(pt.get(i + 1))) { pt.remove(i); } } if(pt.get(0).chonghe(pt.get(pt.size()-1))) { pt.remove(0); } //判斷點在兩點之間 for (int i = 0; i < pt.size(); i++) { if(Line.threeline(pt.get(i%pt.size()),pt.get((i+1)%pt.size()),pt.get((i+2)%pt.size()))) { pt.remove((i+1)%pt.size()); } } } public static double sswr(double s) { String str=String.valueOf(s); String substring = str.substring(str.indexOf(".") + 1); int str_len; if(substring.length()>3) { str_len=3; }else { str_len=substring.length(); } String formats="%."+str_len+"f"; String out=String.format(formats,s); double res=Double.parseDouble(out); return res; } } class Point { private double x; private double y; public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } /*傳入一個點 計算兩點間的距離 返回兩點間距離 */ public double distance(Point a) { double dis; dis = Math.sqrt(Math.pow((a.x - this.x),2) + Math.pow((a.y - this.y),2)); return dis; } public boolean CheckPoint(Point p){ if( Math.abs(this.getX() - p.getX() )< 0.000001 && Math.abs(this.getY() - p.getY() )< 0.000001){ return true; } else return false; } public boolean chonghe(Point a){ if(this.getX() == a.getX() && this.getY() == a.getY()) return true; return false; } } class Line { private Point m,n; private double b;//y=kx+b private double k; private double A; private double B; private double C; public Line() { } public Line(Point m,Point n) { this.m = m; this.n = n; this.slope(); this.equation(m,n);//求出直線方程 } public void setMN(Point m,Point n) { this.m = m; this.n = n; this.slope(); this.equation(m,n);//求出直線方程 } public Point getM() { return m; } public Point getN() { return n; } public double getA() { return A; } public double getC() { return C; } public double getK() { return k; } public double getB() { return B; } //直線的斜率 public void slope() { double se; if(m.getX() == n.getX()) k = POSITIVE_INFINITY; else if(m.getY() == n.getY()) k = 0; else { se = (m.getY()-n.getY())/(m.getX()-n.getX()); k = se; } } public void equation(Point m,Point n) { double b; b = m.getY() - this.k * m.getX(); A = n.getY() - m.getY(); B = m.getX() - n.getX(); C = n.getX() * m.getY() - m.getX() * n.getY(); } //點到直線的距離 double p_to_l(Point a,Line l) { //double dis = Math.abs(l.getA()*a.getX() + l.getB()*a.getY() + l.getC())/Math.sqrt(l.A * l.A + l.B* l.B); //return dis; if(l.k == 0) { return Math.abs(l.getM().getX()-a.getX()); } else if(l.k == 1) { return Math.abs(l.getM().getY()-a.getY()); } else { return Math.abs(l.getK()*a.getX()-a.getY()+ this.b)/(Math.sqrt(1+l.getK()*l.getK())); } } //判斷三點一線,用於判斷選項四的三角形情況 public static boolean threeline(Point a, Point b, Point c) { Line line1 = new Line(); line1.setMN(a,c); return line1.isallline(b) && line1.pointupline(b); } public boolean fourpoint(Line a) { if(Math.abs(a.k - this.k) < 0.000001) return true; else return false; } //求兩直線交點坐標 public Point intersection(Line a) { Point point = new Point(); double det = this.getA() * a.getB() - a.getA() * this.getB(); point.setX(( this.getB() * a.getC() - a.getB() * this.getC() )/det); point.setY(( a.getA() * this.getC() - this.getA() * a.getC() )/det); return point; } //點在線端內,點到線上兩端點的距離==兩端點距離 public boolean pointupline(Point a) { if(Math.abs(a.distance(this.getM()) + a.distance(this.getN()) - this.distance()) < 0.000001) return true; else return false; } //點在線上不包含端點 public boolean pointupline2(Point a) { if(this.pointupline(a) && !this.getM().chonghe(a) && !this.getN().chonghe(a)) return true; return false; } //點是否在直線上 public boolean isallline(Point a) { if(Math.abs( getA() * a.getX() + getB() * a.getY() + getC() ) < 0.000001) return true; return false; } //線段距離 public double distance() { double dis; dis = Math.sqrt(Math.pow((m.getX() - n.getX()),2) + Math.pow((m.getY() - n.getY()),2)); return dis; } //判斷兩點是否在直線一側 public boolean istongce(Point a,Point b) { double x1; double x2; x1 = this.getA() * a.getX() + this.getB() * a.getY() + this.getC(); x2 = this.getA() * b.getX() + this.getB() * b.getY() + this.getC(); if(x1 * x2 > 0) return true; else return false; } //判斷兩條線重合 public boolean chonghe(Line l) { if(this.isallline(l.getM()) && this.isallline(l.getN())) { return true; } return false; } } class triangle { private Line l1 = new Line(); private Line l2 = new Line(); private Line l3 = new Line(); public triangle(Line l1, Line l2, Line l3) { this.l1 = l1; this.l2 = l2; this.l3 = l3; } public triangle(Point a, Point b, Point c) { this.l1.setMN(a, b); this.l2.setMN(b, c); this.l3.setMN(c, a); } public Line getL1() { return l1; } public void setL1(Line l1) { this.l1 = l1; } public Line getL2() { return l2; } public void setL2(Line l2) { this.l2 = l2; } public Line getL3() { return l3; } public void setL3(Line l3) { this.l3 = l3; } //是否能構成三角形 public boolean istriangle() { if (l1.isallline(l2.getN()) || l2.isallline(l3.getN()) || l3.isallline(l1.getN())) return false; return true; } //等腰三角形 public boolean istwoline() { if (Math.abs(l1.distance() - l2.distance()) < 0.000001 || Math.abs(l2.distance() - l3.distance()) < 0.000001 || Math.abs(l2.distance() - l3.distance()) < 0.000001) { return true; } else return false; } //等邊三角形 public boolean threeline() { if (Math.abs(l1.distance() - l2.distance()) < 0.000001 && Math.abs(l1.distance() - l3.distance()) < 0.000001 && Math.abs(l2.distance() - l3.distance()) < 0.000001) { return true; } else return false; } //三角形周長 public double Perimeter() { return l1.distance() + l2.distance() + l3.distance(); } //三角形面積 public double area() { double s = this.Perimeter() * 0.5; return Math.sqrt(s * (s - l1.distance()) * (s - l2.distance()) * (s - l3.distance())); } public double area3(){ return l1.p_to_l(l1.getM(),l1) * l1.distance() *0.5; } public double area2(Point a, Point b, Point c) { double d1, d2, d3; d1 = a.distance(b); d2 = b.distance(c); d3 = a.distance(c); double s = 0.5 * (d1 + d2 + d3); return Math.sqrt(s * (s - d1) * (s - d2) * (s - d3)); } //重心 public Point focus() { Point weight = new Point(); weight.setX((l1.getM().getX() + l1.getN().getX() + l2.getN().getX()) * 1.0 / 3); weight.setY((l1.getM().getY() + l1.getN().getY() + l2.getN().getY()) * 1.0 / 3); return weight; } //求餘弦 public double[] getcos() { double[] cos = new double[3]; cos[0] = (l1.distance() * l1.distance() + l2.distance() * l2.distance() - l3.distance() * l3.distance()) / (2 * l1.distance() * l2.distance()); cos[1] = (l1.distance() * l1.distance() + l3.distance() * l3.distance() - l2.distance() * l2.distance()) / (2 * l1.distance() * l3.distance()); cos[2] = (l3.distance() * l3.distance() + l2.distance() * l2.distance() - l1.distance() * l1.distance()) / (2 * l3.distance() * l2.distance()); return cos; } public double getcos(Point a, Point b, Point c) { double l1 = a.distance(b); double l2 = a.distance(c); double l3 = b.distance(c); return (l1 * l1 + l2 * l2 - l3 * l3) / (2 * l1 * l2); } // 點在三角形的邊上 public boolean pupline(Point a) { if(l1.pointupline(a) && l1.isallline(a)){ return true; } else if(l2.isallline(a) && l2.pointupline(a)) { return true; } else if(l3.pointupline(a) && l3.isallline(a)) { return true; } else return false; } //點在三角形內 public boolean pupin(Point a) { triangle tl1 = new triangle(l1.getM(), l1.getN(), a); triangle tl2 = new triangle(l2.getM(), l2.getN(), a); triangle tl3 = new triangle(l3.getM(), l3.getN(), a); if(!this.pupline(a) && Math.abs(tl1.area() + tl2.area() + tl3.area() - this.area()) < 0.0001) return true; return false; } public boolean chonghe(Line l) { if(l1.chonghe(l)) return true; if(l2.chonghe(l)) return true; if(l3.chonghe(l)) return true; return false; } public void OneTriangle(Line line){ List<Line> lineList = new ArrayList<>(); lineList.add(l1);lineList.add(l2);lineList.add(l3); List<Point> list = new ArrayList<>(); int cnt = 0; Point u; for(int i=0;i<lineList.size();i++){ u = lineList.get(i).intersection(line); boolean flag = false; if( u != null){ if(lineList.get(i).pointupline(u)){ flag = true; } for (Point p : list){ if( p.CheckPoint(u) ){ flag = false; break; } } if(flag){ list.add(u); //System.out.println(u.getX() + " " + u.getY() ); cnt++; } } } if(cnt < 2){ System.out.println(cnt); } else { double s1,s2,s; System.out.print("2 "); Line lline = new Line(list.get(0), list.get(1)); Point p1 = list.get(0),p2 = list.get(1); Point m; if(l1.isallline(p1) && l2.isallline(p2) || l2.isallline(p2) && l1.isallline(p1)) m = l1.getN(); else if( l1.isallline(p1) && l3.isallline(p2) || l3.isallline( p2) && l1.isallline(p1) ) m = l1.getM(); else m = l2.getN(); triangle triangle1 = new triangle(m,list.get(0),list.get(1)); s1 = triangle1.area(); s1 = Judge.sswr(s1); s = this.area(); s = Judge.sswr(s); s2 = s - s1; s2 = Judge.sswr(s2); System.out.println(Math.min(s1,s2) + " " + Math.max(s1,s2)); } } } class quadrilateral { private Line line01; private Line line02; private Line line03; private Line line04; Point[] point = new Point[4]; public quadrilateral(Point a,Point b,Point c,Point d) { point[0] = a;point[1] = b;point[2] = c; point[3] = d; Line line01 = new Line(a,b); this.line01 = line01; Line line02 = new Line(b,c); this.line02 = line02; Line line03 = new Line(c,d); this.line03 = line03; Line line04 = new Line(d,a); this.line04 = line04; } public boolean isquadrilateral() { if((line01.getK() == line02.getK() || line02.getK() == line03.getK() || line03.getK() == line04.getK() || line04.getK() == line01.getK()) || (line01.pointupline(line01.intersection(line03)) && line03.pointupline(line01.intersection(line03))) || (line02.pointupline(line02.intersection(line04)) && line04.pointupline(line02.intersection(line04)))) { return false; } else { return true; } } public boolean ispingxing() { if(line01.getK() == line03.getK() && line02.getK() == line04.getK()){ return true; } else return false; } public boolean islingxing() { if(this.ispingxing() && this.line01.distance() == this.line02.distance() && this.line01.distance() == this.line03.distance() && this.line01.distance() == this.line04.distance()) { return true; } else return false; } public boolean isjuxing() { if(this.ispingxing() && ( (this.line01.getK() == POSITIVE_INFINITY && this.line02.getK() == 0) || (this.line01.getK() == 0 && this.line02.getK() == POSITIVE_INFINITY) || this.line01.getK() * this.line02.getK() == -1)) { return true; } else return false; } public boolean iszhengfangxing() { if(this.isjuxing() && this.islingxing()) { return true; } else return false; } //判斷凸四邊形 public boolean istusibainxing() { if(line01.istongce(line03.getM(),line03.getN()) && line02.istongce(line04.getM(),line04.getN()) && line03.istongce(line01.getM(),line01.getN()) && line04.istongce(line02.getM(),line02.getN())) { return true; } else return false; } //四邊形周長 public double perimeter() { return line01.distance() + line02.distance() + line03.distance() + line04.distance(); } //四邊形面積 public double area() { triangle triangle01 = new triangle(line01.getM(), line01.getN(), line02.getN()); triangle triangle02 = new triangle(line03.getM(), line03.getN(), line04.getN()); triangle triangle03 = new triangle(line02.getM(), line02.getN(), line03.getN()); triangle triangle04 = new triangle(line04.getM(), line04.getN(), line01.getN()); double qarea01,qarea02; qarea01 = triangle01.area() + triangle02.area(); qarea02 = triangle03.area() + triangle04.area(); if(qarea02 < qarea01)//凹四邊形面積比較特殊,要找凹點,這裡偷懶直接判段小的輸出 return qarea02; else return qarea01; } //點在四邊形邊上 public boolean pupline(Point a) { if(line01.pointupline(a) && line01.isallline(a)) return true; else if(line02.pointupline(a) && line02.isallline(a)) return true; else if(line03.pointupline(a) && line03.isallline(a)) return true; else if(line04.pointupline(a) && line04.isallline(a)) return true; else return false; } //點在四邊形內部 public boolean pupin(Point a) { triangle tl01 = new triangle(line01.getM(), line01.getN(), a); triangle tl02 = new triangle(line02.getM(), line02.getN(), a); triangle tl03 = new triangle(line03.getM(), line03.getN(), a); triangle tl04 = new triangle(line04.getM(), line04.getN(), a); if(!this.pupline(a) && Math.abs(tl01.area() + tl02.area() + tl03.area() + tl04.area() - this.area()) < 0.0001) return true; else return false; } public boolean chonghe(Line l) { if(line01.chonghe(l)) return true; if(line02.chonghe(l)) return true; if(line03.chonghe(l)) return true; if(line04.chonghe(l)) return true; return false; } //四邊形分割成兩個求面積,有兩個交點 public void fengeArea(Point a,Point b,Point c) { triangle tr1 = new triangle(a,b,c); double area1 = tr1.area(); double area = this.area(); double area2 = area - area1; area1 = Judge.sswr(area1); area2 = Judge.sswr(area2); System.out.println("2 " + Math.min(area1,area2) + " " + Math.max(area1,area2)); } public void Onequarilateral(Line l) { Point[] points = new Point[4]; ArrayList<Line> lines = new ArrayList<>(); lines.add(line01);lines.add(line02);lines.add(line03);lines.add(line04); int[] p_in = new int[4]; //判斷交點在線上還是端點 for (int i = 0; i < 4; i++) { p_in[i] = 0; //求直線與四邊形的交點 points[i] = lines.get(i).intersection(l); if(points[i]!=null) { //判斷交點是否在邊上,不包括端點 if(lines.get(i).pointupline2(points[i])) p_in[i] = 1; } } //有頂角在線上 for (int i = 0; i < 4; i++) { if(l.isallline(point[i])) { if(l.isallline((point[(i+2)%4]))) { fengeArea(point[i], point[(i + 2) % 4], point[(i + 1) % 4]); return; } else if(p_in[(i+1)%4] == 1) { fengeArea(point[i], point[(i + 1) % 4], points[(i + 1) % 4]); return; } else if(p_in[(i+2)%4] == 1) { fengeArea(point[i], point[(i + 3) % 4], points[(i + 2) % 4]); return; } else { System.out.println("1"); return; } } } //兩個臨邊 for (int i = 0; i < 4; i++) { if(p_in[i] == 1 && p_in[(i+1)%4] == 1) { fengeArea(point[(i + 1) % 4], points[i], points[(i + 1) % 4]); return; } } //兩個對邊 for (int i = 0; i < 2; i++) { if(p_in[i] == 1 && p_in[i+2] == 1) { triangle tr1 = new triangle(point[i], points[i], points[(i + 2) % 4]); triangle tr2 = new triangle(point[(i+3)%4], point[i], points[(i + 2) % 4]); double area1 = tr1.area() + tr2.area(); double area = this.area(); double area2 = area - area1; area1 = Judge.sswr(area1); area2 = Judge.sswr(area2); System.out.println("2 " + Math.min(area1,area2) + " " + Math.max(area1,area2)); return; } } System.out.println("0"); return; } }
先利用check方法(正則表達式)檢查一下輸入進來的字元串,然後根據第一位是什麼數字進入執行對應的方法。
用戶輸入一組選項和數據,進行與五邊形有關的計算。
以下五邊形頂點的坐標要求按順序依次輸入,連續輸入的兩個頂點是相鄰頂點,第一個和最後一個輸入的頂點相鄰。
選項包括:
1:輸入五個點坐標,判斷是否是五邊形,判斷結果輸出true/false。
2:輸入五個點坐標,判斷是凹五邊形(false)還是凸五邊形(true),如果是凸五邊形,則再輸出五邊形周長、面積,結果之間以一個英文空格符分隔。 若五個點坐標無法構成五邊形,輸出”not a pentagon”
3:輸入七個點坐標,前兩個點構成一條直線,後五個點構成一個凸五邊形、凸四邊形或凸三角形,輸出直線與五邊形、四邊形或三角形相交的交點數量。如果交點有兩個,再按面積從小到大輸出被直線分割成兩部分的面積(不換行)。若直線與多邊形形的一條邊線重合,輸出”The line is coincide with one of the lines”。若後五個點不符合五邊形輸入,若前兩點重合,輸出”points coincide”。
以上3選項中,若輸入的點無法構成多邊形,則輸出”not a polygon”。輸入的五個點坐標可能存在冗餘,假設多邊形一條邊上兩個端點分別是x、y,邊線中間有一點z,另一頂點s:
1)符合要求的輸入:頂點重複或者z與xy都相鄰,如:x x y s、x z y s、x y x s、s x y y。此時去除冗餘點,保留一個x、一個y。
2) 不符合要求的輸入:z不與xy都相鄰,如:z x y s、x z s y、x s z y
輸入格式:
基本格式:選項+”:”+坐標x+”,”+坐標y+” “+坐標x+”,”+坐標y。點的x、y坐標之間以英文”,”分隔,點與點之間以一個英文空格分隔。
輸出格式:
基本輸出格式見每種選項的描述。
異常情況輸出:
如果不符合基本格式,輸出”Wrong Format”。
如果符合基本格式,但輸入點的數量不符合要求,輸出”wrong number of points”。
注意:輸出的數據若小數點後超過3位,只保留小數點後3位,多餘部分採用四捨五入規則進到最低位。小數點後若不足3位,按原始位數顯示,不必補齊。例如:1/3的結果按格式輸出為 0.333,1.0按格式輸出為1.0
輸入樣例1:
選項1,點重合。例如:
1:-1,-1 1,2 -1,1 1,0
輸出樣例:
在這裡給出相應的輸出。例如:
wrong number of points
詳細資訊及樣例請查看附件,本題包含附件中的選項1-3的功能:
類圖:

程式碼軟體分析:

程式碼主要類:
public static boolean geshi(String s){ String s2= s.substring(0,2); if(!s2.matches("[1-6]\\:")) { System.out.println("Wrong Format"); return false; } String s3 = s.substring(2); if(!s3.matches("([+|-]?(0|[1-9][0-9]*)(\\.\\d+)?,[+|-]?(0|[1-9][0-9]*)(\\.\\d+)?\\ ?)+")) { System.out.println("Wrong Format"); return false; } return true; } public static boolean dianshu(String s){ String[] a = s.split(":"); String[] b = a[1].split(" "); int n = b.length; if (s.charAt(0) == '1' && n != 5) { System.out.println("wrong number of points"); return false; } else if (s.charAt(0) == '2' && n != 5) { System.out.println("wrong number of points"); return false; } else if (s.charAt(0) == '3' && n != 7) { System.out.println("wrong number of points"); return false; } else if (s.charAt(0) == '4' && n != 10) { System.out.println("wrong number of points"); return false; } else if (s.charAt(0) == '6' && n != 6) { System.out.println("wrong number of points"); return false; } return true; } static class Wubianxing { Point a,b,c,d,e; Line ab,bc,cd,de,ea,ac,ad,bd,be,ce; Wubianxing(Point a,Point b,Point c,Point d,Point e){ this.a=a;this.b=b;this.c=c;this.d=d;this.e=e; this.ab=new Line(a,b); this.bc=new Line(b,c); this.cd=new Line(c,d); this.de=new Line(d,e); this.ea=new Line(e,a); this.ac=new Line(a,c); this.ad=new Line(a,d); this.bd=new Line(b,d); this.be=new Line(b,e); this.ce=new Line(c,e); } public boolean iswubianxing(){ if(ab.pingxing(bc)||bc.pingxing(cd)||cd.pingxing(de)||de.pingxing(ea)){ return false; } else if(Line.intersect(a.x,a.y,b.x,b.y,c.x,c.y,d.x,d.y)||Line.intersect(a.x,a.y,b.x,b.y,d.x,d.y,e.x,e.y)|| Line.intersect(b.x,b.y,c.x,c.y,d.x,d.y,e.x,e.y)||Line.intersect(b.x,b.y,c.x,c.y,e.x,e.y,a.x,a.y)|| Line.intersect(c.x,c.y,d.x,d.y,e.x,e.y,a.x,a.y)) return false; return true; } public boolean istuwubianxing(){ if((((b.x-a.x)*(c.y-b.y))-((c.x-b.x)*(b.y-a.y))>0&&((c.x-b.x)*(d.y-c.y))-((d.x-c.x)*(c.y-b.y))>0&& ((d.x-c.x)*(e.y-d.y))-((e.x-d.x)*(d.y-c.y))>0&&((e.x-d.x)*(a.y-e.y))-((a.x-e.x)*(e.y-d.y))>0)|| (((b.x-a.x)*(c.y-b.y))-((c.x-b.x)*(b.y-a.y))<0&&((c.x-b.x)*(d.y-c.y))-((d.x-c.x)*(c.y-b.y))<0&& ((d.x-c.x)*(e.y-d.y))-((e.x-d.x)*(d.y-c.y))<0&&((e.x-d.x)*(a.y-e.y))-((a.x-e.x)*(e.y-d.y))<0)) return true; else return false; } public double zhouchang(){ double c=this.ab.length()+this.bc.length()+this.cd.length()+this.de.length()+this.ea.length(); double C=outformat(c); return C; } public double area(){ Sanjiao san1=new Sanjiao(this.a,this.b,this.c); Sanjiao san2=new Sanjiao(this.a,this.c,this.d); Sanjiao san3=new Sanjiao(this.a,this.d,this.e); double mj= san1.mianji()+ san2.mianji()+ san3.mianji(); double mianji=outformat(mj); return mianji; } public Double outformat(double num) { if(num*1e+3%10!=0) { String num1=String.format("%.3f",num); return Double.valueOf(num1); } return num; } public boolean bianchonghe (Line l){ if(this.ab.xianchonghe(l)){ return true; } else if(this.bc.xianchonghe(l)){ return true; } else if(this.cd.xianchonghe(l)){ return true; } else if(this.de.xianchonghe(l)){ return true; } else if(this.ea.xianchonghe(l)){ return true; } return false; } public void fengewubainxing(Line l) { double area1=0,area2=0; if(this.ac.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.a,this.b,this.c); area1=ss1.mianji(); area2=this.area()-area1; out(area1,area2); } else if(this.ad.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.a,this.d,this.e); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bd.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.b,this.d,this.c); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.be.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.a,this.b,this.e); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ce.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.c,this.d,this.e); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.bc.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.bc.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.b,this.bc.jiaodian(l)); area1= ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.ab.jiaodian(l),this.b,this.c,this.cd.jiaodian(l)); ss1.otupanduan(); area1= ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.de.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.a,this.ab.jiaodian(l),this.de.jiaodian(l),this.e); ss1.otupanduan(); area1= ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.ea.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.a,this.ea.jiaodian(l)); area1= ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bc.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null&&this.bc.jiaodian(l)!=this.cd.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.bc.jiaodian(l),this.c,this.cd.jiaodian(l)); area1= ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bc.jiaodian(l)!=null&&this.de.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.bc.jiaodian(l),this.c,this.d,this.de.jiaodian(l)); ss1.otupanduan(); area1= ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bc.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.bc.jiaodian(l),this.ea.jiaodian(l),this.a,this.b); ss1.otupanduan(); area1= ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.cd.jiaodian(l)!=null&&this.de.jiaodian(l)!=null&&this.cd.jiaodian(l)!=this.de.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.cd.jiaodian(l),this.d,this.de.jiaodian(l)); area1= ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.cd.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.cd.jiaodian(l),this.ea.jiaodian(l),this.e,this.d); ss1.otupanduan(); area1= ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.de.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null&&this.ea.jiaodian(l)!=this.de.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.ea.jiaodian(l),this.e,this.de.jiaodian(l)); area1= ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else { System.out.println(0); System.exit(0); } } public void out(double m1,double m2){ if(m1>=m2){ System.out.println(2+" "+m2+" "+m1); System.exit(0); } else{ System.out.println(2+" "+m1+" "+m2); System.exit(0); } } public boolean inwubianxing(Point p){ Sanjiao ss1=new Sanjiao(this.a,this.b,p);Sanjiao ss2=new Sanjiao(this.b,this.c,p); Sanjiao ss3=new Sanjiao(this.c,this.d,p);Sanjiao ss4=new Sanjiao(this.d,this.e,p); Sanjiao ss5=new Sanjiao(this.e,this.a,p); if(Math.abs(this.area()-(ss1.mianji()+ss2.mianji()+ss3.mianji()+ss4.mianji()+ss5.mianji()))<0.0001) return true; else return false; } } static class Line { Point x,y; Line (Point a, Point b){ this.x=a; this.y=b; } double length(){ return this.x.juli(this.y); } double distance(Point p){//!!! if(this.x.x==this.y.x){ return (p.x-this.x.x); } else{ double e=(this.x.y-this.y.y)/(this.x.x-this.y.x); double b=this.x.y-(e*this.x.x); return (e*p.x-p.y+b)/Math.sqrt(e*e+1); } } public static boolean intersect(double l1x1,double l1y1,double l1x2,double l1y2,double l2x1,double l2y1,double l2x2,double l2y2) { // 快速排斥實驗 首先判斷兩條線段在 x 以及 y 坐標的投影是否有重合。 有一個為真,則代表兩線段必不可交。 if (Math.max(l1x1,l1x2) < Math.min(l2x1 ,l2x2) || Math.max(l1y1,l1y2) < Math.min(l2y1,l2y2) || Math.max(l2x1,l2x2) < Math.min(l1x1,l1x2) || Math.max(l2y1,l2y2) < Math.min(l1y1,l1y2)) { return false; } // 跨立實驗 如果相交則矢量叉積異號或為零,大於零則不相交 else if ((((l1x1 - l2x1) * (l2y2 - l2y1) - (l1y1 - l2y1) * (l2x2 - l2x1)) * ((l1x2 - l2x1) * (l2y2 - l2y1) - (l1y2 - l2y1) * (l2x2 - l2x1))) > 0 || (((l2x1 - l1x1) * (l1y2 - l1y1) - (l2y1 - l1y1) * (l1x2 - l1x1)) * ((l2x2 - l1x1) * (l1y2 - l1y1) - (l2y2 - l1y1) * (l1x2 - l1x1))) > 0) { return false; } return true; } public double duijiaoxian() { double duijiaoxian=Math.sqrt((this.x.x-this.y.x)*(this.x.x-this.y.x)+(this.x.y-this.y.y)*(this.x.y-this.y.y)); return duijiaoxian; } public boolean xianchonghe (Line l){ return this.pingxing(l)&&l.distance(this.x)==0; } boolean inline(Point p){ if(this.x.x==this.y.x&&this.y.x==p.x) return true; double e=(this.x.y-this.y.y)/(this.x.x-this.y.x); double b=this.x.y-(e*this.x.x); if((((e*p.x-p.y+b)==0&&(p.x>=min(x.x,y.x)&&p.x<=max(x.x,y.x)))&&((e*p.x-p.y+b)==0&&(p.y>=min(x.y,y.y)&&p.y<=max(x.y,y.y))))) return true; else return false; } Point jiaodian(Line l){ Point v=sub(l.y,l.x); Point w=sub(this.y,this.x); Point p=l.x; Point q=this.x; Point u=sub(p,q); double t=cross(w,u)/cross(v,w); Point ans =new Point( p.x+v.x*t,p.y+v.y*t); double y0=ans.y; double x0=ans.x; if(((x0)>=min(x.x,y.x)&&(x0)<=max(x.x,y.x))&&((y0)>=min(x.y,y.y)&&(y0)<=max(x.y,y.y))) return ans; return null; } public static double cross (Point a, Point b){ return a.x*b.y-a.y*b.x; } public static Point sub(Point a, Point b){ return new Point(a.x-b.x,a.y-b.y); } boolean pingxing (Line a){ if((a.x.x==a.y.x )&&(this.x.x==this.y.x)) return true; if((a.x.x==a.y.x)&&(this.x.x!=this.y.x)) return false; if((a.x.x!=a.y.x)&&(this.x.x==this.y.x)) return false; double e=a.x.xilv(a.y); double e1=this.x.xilv(this.y); if(e==e1) return true; else return false; } } static class Point { double x,y; Point(double a,double b){ this.x=a; this.y=b; } public double getx(){ return x; } public double gety(){ return y; } public double juli(Point p){ return Math.sqrt((this.x-p.x )*(this.x-p.x )+(this.y-p.y )*(this.y-p.y)); } public double xilv(Point p){ if(this.x==p.x){ System.out.println("Slope does not exist"); System.exit(0); } return (this.y-p.y)/(this.x-p.x); } } static class Sanjiao { Main.Point sx,sy,sz; Main.Line sa,sb,sc; Sanjiao (Main.Point a, Main.Point b, Main.Point c){ this.sx=a; this.sy=b; this.sz=c; this.sa=new Main.Line(b,c); this.sb=new Main.Line(a,c); this.sc=new Main.Line(a,b); } public boolean gouchengsanjiao(){ if(((this.sa.length()+this.sb.length())<=this.sc.length())||((this.sa.length()+this.sc.length())<=this.sb.length())||((this.sb.length()+this.sc.length())<=this.sa.length())){ return false; } else return true; } public double zhouchang(){ return (this.sa.length()+this.sb.length()+this.sc.length()); } public double mianji(){ double area=0; double s=(this.sa.length()+this.sb.length()+this.sc.length())/2; return area=Math.sqrt(s*(s-this.sa.length())*(s-this.sb.length())*(s-this.sc.length())); } public int type(){ double[] num = new double[3]; num[0] = this.sa.length();num[1] = this.sb.length();num[2] = this.sc.length(); Arrays.sort(num); double tmp = Math.pow(num[0],2) + Math.pow(num[1],2) - Math.pow(num[2],2); if(Math.abs(tmp) < 0.0000001) return 1; if(tmp < 0) return 2; return 0; } public boolean insanjiao(Main.Point p){ Sanjiao san1=new Sanjiao(p,sx,sy); Sanjiao san2=new Sanjiao(p,sy,sz); Sanjiao san3=new Sanjiao(p,sz,sx); double m1=san1.mianji(); double m2=san2.mianji(); double m3=san3.mianji(); if(Math.abs(this.mianji()-(m1+m2+m3))<0.0001) return true; else return false; } public void fengesanjiaoxing(Line l){ double area1=0,area2=0; if(this.sc.jiaodian(l)!=null&&this.sa.jiaodian(l)!=null&&this.sc.jiaodian(l)!=this.sa.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.sc.jiaodian(l),this.sy,this.sa.jiaodian(l)); area1=ss1.mianji(); area2=this.mianji()-area1; double mj1=outformat( area1); double mj2=outformat( area2); out(mj1,mj2); } else if(this.sc.jiaodian(l)!=null&&this.sb.jiaodian(l)!=null&&this.sc.jiaodian(l)!=this.sb.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.sc.jiaodian(l),this.sb.jiaodian(l),this.sx); area1=ss1.mianji(); area2=this.mianji()-area1; double mj1=outformat( area1); double mj2=outformat( area2); out(mj1,mj2); } else if(this.sa.jiaodian(l)!=null&&this.sb.jiaodian(l)!=null&&this.sa.jiaodian(l)!=this.sb.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.sa.jiaodian(l),this.sz,this.sb.jiaodian(l)); area1=ss1.mianji(); area2=this.mianji()-area1; double mj1=outformat( area1); double mj2=outformat( area2); out(mj1,mj2); } else { System.out.println(0); System.exit(0); } } public Double outformat(double num) { if(num*1e+3%10!=0) { String num1=String.format("%.3f",num); return Double.valueOf(num1); } return num; } public void out(double m1,double m2){ if(m1>=m2){ System.out.println(2+" "+m2+" "+m1); System.exit(0); } else{ System.out.println(2+" "+m1+" "+m2); System.exit(0); } } public boolean bianchonghe(Line l){ if(this.sa.xianchonghe(l)) return false; else if(this.sb.xianchonghe(l)) return false; else if(this.sc.xianchonghe(l)) return false; else return true; } } static class Sibian { Main.Point a,b,c,d; Main.Line ab,bc,cd,da,ac,bd; private boolean judge1=false;//0,2 private boolean judge2=false;//1,3 Sibian(Main.Point a, Main.Point b, Main.Point c, Main.Point d){ this.a=a;this.b=b;this.c=c;this.d=d; this.ab=new Main.Line(a,b); this.bc=new Main.Line(b,c); this.cd=new Main.Line(c,d); this.da=new Main.Line(d,a); this.ac=new Main.Line(a,c); this.bd=new Main.Line(b,d); } public void sibianxing(){ if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6|| Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6|| Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6|| Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6)System.out.print("false "); else { if(!Main.Line.intersect(a.x,a.y,d.x,d.y,b.x,b.y,c.x,c.y)) { System.out.print("true "); } else System.out.print("false "); } } public void pingxingsibianxing(){ if(this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length())System.out.print("true"); else System.out.print("false"); } public boolean nengfougoucheng(){ if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6|| Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6|| Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6|| Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6) { return false; } else return !Main.Line.intersect(a.x, a.y, d.x, d.y, b.x, b.y, c.x, c.y) && !Main.Line.intersect(a.x, a.y, b.x, b.y, d.x, d.y, c.x, c.y); } public boolean lingxing(){ return (this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length()); } public boolean changfangxing(){ Main.Line l1=new Main.Line(a,c); double ac=l1.duijiaoxian(); Main.Line l2=new Main.Line(b,d); double bd=l2.duijiaoxian(); return (ac==bd&&this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length()); } public boolean zhengfangxing(){ return (lingxing()&& changfangxing()); } public boolean otupanduan() { Main.Line l1=new Main.Line(a,c); double distance1=l1.distance(b); double distance2=l1.distance(d); Main.Line l2=new Main.Line(b,d); double distance3=l2.distance(a); double distance4= l2.distance(c); if(distance1*distance2<0)judge1=true; if(distance3*distance4<0)judge2=true; if(judge1==true&&judge2==true) { return true; } return false; } public double zhouchang() { double ab=this.ab.length(); double bc=this.bc.length(); double cd=this.cd.length(); double da=this.da.length(); double c=ab+bc+cd+da; double C=outformat(c); return C; } public double area() { double area=0; double area1=0; double area2=0; double are=0; //凸四邊形 if(judge1==true&&judge2==true) { area1=Math.abs((b.x*c.y+c.x*d.y+d.x*b.y-b.x*d.y-c.x*b.y-d.x*c.y)/2); area2=Math.abs((b.x*a.y+a.x*d.y+d.x*b.y-b.x*d.y-a.x*b.y-d.x*a.y)/2); area=area1+area2; are= outformat(area); } else if(judge1==false) { area1=Math.abs((b.x*d.y+d.x*a.y+a.x*b.y-b.x*a.y-d.x*b.y-a.x*d.y)/2); area2=Math.abs((d.x*c.y+c.x*b.y+b.x*d.y-d.x*b.y-c.x*d.y-b.x*c.y)/2); area=area1+area2; are= outformat(area); } else if(judge2==false) { area1=Math.abs((b.x*c.y+c.x*a.y+a.x*b.y-b.x*a.y-c.x*b.y-a.x*c.y)/2); area2=Math.abs((d.x*c.y+c.x*a.y+a.x*d.y-d.x*a.y-c.x*d.y-a.x*c.y)/2); area=area1+area2; are=outformat(area); } return are; } public Double outformat(double num) { if(num*1e+3%10!=0) { String num1=String.format("%.3f",num); return Double.valueOf(num1); } return num; } public boolean bianchonghe (Main.Line l){ if(this.ab.xianchonghe(l)){ return true; } else if(this.bc.xianchonghe(l)){ return true; } else if(this.cd.xianchonghe(l)){ return true; } else if(this.da.xianchonghe(l)){ return true; } return false; } public boolean insibian(Main.Point p){ double m=0; if(otupanduan()){ m=area(); } Main.Sanjiao ss1=new Main.Sanjiao(p,a,b); Main.Sanjiao ss2=new Main.Sanjiao(p,b,c); Main.Sanjiao ss3=new Main.Sanjiao(p,c,d); Main.Sanjiao ss4=new Main.Sanjiao(p,d,a); double m1=ss1.mianji(); double m2=ss2.mianji(); double m3=ss3.mianji(); double m4=ss4.mianji(); if(Math.abs(m-(m1+m2+m3+m4))<0.0001)/*注意一定要三位小數或更多,不然通不過測試點*/ return true; else return false; } public void fengesibianxing(Line l){ double area1=0,area2=0; if(this.ac.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.a,this.b,this.c); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bd.xianchonghe(l)){ Sanjiao ss1=new Sanjiao(this.a,this.b,this.d); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.bc.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.bc.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.b,this.bc.jiaodian(l)); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.a,this.ab.jiaodian(l),this.cd.jiaodian(l),this.d); area1=ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.ab.jiaodian(l)!=null&&this.da.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.da.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.a,this.ab.jiaodian(l),this.da.jiaodian(l)); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bc.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null&&this.bc.jiaodian(l)!=this.cd.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.bc.jiaodian(l),this.c,this.cd.jiaodian(l)); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.bc.jiaodian(l)!=null&&this.da.jiaodian(l)!=null){ Sibian ss1=new Sibian(this.a,this.b,this.bc.jiaodian(l),this.da.jiaodian(l)); area1=ss1.area(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else if(this.cd.jiaodian(l)!=null&&this.da.jiaodian(l)!=null&&this.da.jiaodian(l)!=this.cd.jiaodian(l)){ Sanjiao ss1=new Sanjiao(this.da.jiaodian(l),this.d,this.cd.jiaodian(l)); area1=ss1.mianji(); area2=this.area()-area1; double mj1= outformat(area1); double mj2= outformat(area2); out(mj1,mj2); } else { System.out.println(0); System.exit(0); } } public void out(double m1,double m2){ if(m1>=m2){ System.out.println(2+" "+m2+" "+m1); System.exit(0); } else{ System.out.println(2+" "+m1+" "+m2); System.exit(0); } } } }
思路是是先判斷多邊形多個點分別在線的哪一側,讓在同一側的點與線的交點組成多邊形,任何運用多邊形類裡面的方法,求出相應結果。
用戶輸入一組選項和數據,進行與五邊形有關的計算。
以下五邊形頂點的坐標要求按順序依次輸入,連續輸入的兩個頂點是相鄰頂點,第一個和最後一個輸入的頂點相鄰。
選項包括:
4:輸入十個點坐標,前、後五個點分別構成一個凸多邊形(三角形、四邊形、五邊形),判斷它們兩個之間是否存在包含關係(一個多邊形有一條或多條邊與另一個多邊形重合,其他部分都包含在另一個多邊形內部,也算包含)。
兩者存在六種關係:1、分離(完全無重合點) 2、連接(只有一個點或一條邊重合) 3、完全重合 4、被包含(前一個多邊形在後一個多邊形的內部)5、交錯 6、包含(後一個多邊形在前一個多邊形的內部)。
各種關係的輸出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:輸入十個點坐標,前、後五個點分別構成一個凸多邊形(三角形、四邊形、五邊形),輸出兩個多邊形公共區域的面積。註:只考慮每個多邊形被另一個多邊形分割成最多兩個部分的情況,不考慮一個多邊形將另一個分割成超過兩個區域的情況。
6:輸入六個點坐標,輸出第一個是否在後五個點所構成的多邊形(限定為凸多邊形,不考慮凹多邊形),的內部(若是五邊形輸出in the pentagon/outof the pentagon,若是四邊形輸出in the quadrilateral/outof the quadrilateral,若是三角形輸出in the triangle/outof the triangle)。輸入入錯存在冗餘點要排除,冗餘點的判定方法見選項5。如果點在多邊形的某條邊上,輸出”on the triangle/on the quadrilateral/on the pentagon”。
以上4、5、6選項輸入的五個點坐標可能存在冗餘,假設多邊形一條邊上兩個端點分別是x、y,邊線中間有一點z,另一頂點s:
1)符合要求的輸入:頂點重複或者z與xy都相鄰,如:x x y s、x z y s、x y x s、s x y y。此時去除冗餘點,保留一個x、一個y。
2) 不符合要求的輸入:z不與xy都相鄰,如:z x y s、x z s y、x s z y
輸入格式:
基本格式:選項+”:”+坐標x+”,”+坐標y+” “+坐標x+”,”+坐標y。點的x、y坐標之間以英文”,”分隔,點與點之間以一個英文空格分隔。
輸出格式:
輸出的數據若小數點後超過3位,只保留小數點後3位,多餘部分採用四捨五入規則進到最低位。小數點後若不足3位,按原始位數顯示,不必補齊。例如:1/3的結果按格式輸出為 0.333,1.0按格式輸出為1.0
輸入樣例:
在這裡給出一組輸入。例如:
4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6
輸出樣例:
在這裡給出相應的輸出。例如:
the previous pentagon coincides with the following pentagon
更多樣例請查看附件:
點線形系列5-五邊形題目詳情.pdf


class Point{ public double x, y; public Point(){ this.x = 0; this.y = 0; } public Point(double a,double b){ this.x = a; this.y = b; } public void print(){ String x = String.format("%.6f",this.x); String y = String.format("%.6f",this.y); x = x.replaceAll("0+?$", ""); y = y.replaceAll("0+?$", ""); System.out.printf("(%s , %s)\n",this.x,this.y); } //兩點坐標相同 public boolean isSameTo(Point a){ return (this.x == a.x)&&(this.y == a.y); } //兩點距離 public double disToPoint(Point another){ return Math.sqrt(Math.pow(this.x-another.x,2) + Math.pow(this.y-another.y,2)); } //點到直線的垂直距離 public double disToLine(Line l){ return Math.abs(l.a*this.x+l.b*this.y+l.c) / Math.sqrt(Math.pow(l.a,2)+Math.pow(l.b,2)); } //判斷是否在直線之上 public boolean inLine(Line l){ return Math.abs(l.a*this.x + l.b*this.y + l.c) < 0.000001; } //判斷是否在線段之內(包括端點) public boolean inLineSegment_close(Line l){ if(!this.inLine(l)) return false; double res = this.disToPoint(l.sta) + this.disToPoint(l.ed) - l.length(); return Math.abs(res) < 0.000001; } //判斷是否在線段之內(不包括端點) public boolean inLineSegment(Line l){ return this.inLineSegment_close(l) && (!this.isSameTo(l.sta)) && (!this.isSameTo(l.ed)); } public Point deepCopy(){ Point res = new Point(); res.x = this.x; res.y = this.y; return res; } public Point add(Point another){ Point res = this.deepCopy(); res.x += another.x; res.y += another.y; return res; } public Point sub(Point another){ Point res = this.deepCopy(); res.x -= another.x; res.y -= another.y; return res; } //求點集重心 public static Point focusPoint(Point[] points ){ Point res = new Point(0,0); for(Point item:points){ res = res.add(item); } res.x /= points.length; res.y /= points.length; return res; } } class Graphical { public int len=0,status=1; //多邊形邊數,狀態 public Point[] points; public Line[] lines; public double sideLength = 0,area = 0; //邊長,面積 public boolean isConvexGraphical = true; public String message = "init"; //資訊 public Graphical(Point[] points){ this.points = new Point[points.length]; points = this.removeMulti(points); //去除重複點 if(points.length <=2 ){ this.status = -1; this.message = "Not enough points"; return; } //相鄰邊夾角0則去除中間點,夾角180則status:-1 for(int i=0;i<points.length;i++){ int first = i , second = (i+1)%points.length, third = (i+2)%points.length; try{ Line l1 = new Line(points[first],points[second]); Line l2 = new Line(points[second],points[third]); if( Math.abs(l1.vectorAngle(l2) - Math.PI) < 0.000001 ){ //夾角180 this.status = -1; this.message = "lines reverse coincidence"; return; } else if(Math.abs(l1.vectorAngle(l2)) > 0.000001){ //夾角不為0 this.points[this.len++] = points[second].deepCopy(); } }catch (Exception e){} } this.points = Arrays.copyOf(this.points,this.len); this.lines = new Line[this.len]; //初始化邊 for(int i=0;i<this.len;i++){ try { int first = i, second = (i+1)%this.len; this.lines[i] = new Line(this.points[first], this.points[second]); }catch (Exception e){} } //判斷任意不相鄰邊(線段交點)是否有交點 checkEdge(); Graphical.area(this); Graphical.sideLength(this); Graphical.checkConvex(this); } public void print(){ if(this.status == -1){ System.out.println(this.message); return; } System.out.println("點數為:"+this.len); for(int i=0;i<this.len;i++){ this.points[i].print(); } for(int i=0;i<this.len;i++){ this.lines[i].print(); } System.out.println("周長為:"+this.sideLength); System.out.println("面積為:"+this.area); System.out.println("凹凸性:"+this.isConvexGraphical); } //判斷圖形是否包含某個點返回值-1,0,1 (內部,邊緣,外部) //由於只考慮凸多邊形,用面積法就行 public int isContainPoint(Point p){ for(int i=0;i<this.len;i++){ //位於邊之上 if(p.inLineSegment_close(this.lines[i])) return 0; } double s = 0; for(int i=0;i<this.len;i++){ s += Triangle.area(p,this.points[i], this.points[(i+1)%this.len]); } return Math.abs(s-this.area) < 0.000001 ? -1:1; } //判斷兩個圖形類之間的關係() public String relationshipWith(Graphical g){ String[] name = new String[]{"triangle", "quadrilateral", "pentagon"}; //分離 if(this.isSeparatedFrom(g)){ return "no overlapping area between the previous "+name[this.len-3]+ " and the following "+name[g.len-3]; } //完全重合 if(this.isSameTo(g)) return "the previous "+name[this.len-3]+ " coincides with the following "+name[g.len-3]; //包含 if(this.isContainGra(g)){ return "the previous "+name[this.len-3]+ " contains the following "+name[g.len-3]; } //被包含 if(g.isContainGra(this)){ return "the previous "+name[this.len-3]+ " is inside the following "+name[g.len-3]; } //連接 if(this.overlappingArea(g) == 0){ return "the previous "+name[this.len-3]+ " is connected to the following "+name[g.len-3]; } //交錯 return "the previous "+name[this.len-3]+ " is interlaced with the following "+name[g.len-3]; } //判斷和另一個圖形完全分離(重疊面積為0,並且任意點都在this之外) public boolean isSeparatedFrom(Graphical g){ boolean ok = true; int[] check2 = new int[g.len]; for(int i=0;i<g.len;i++){ check2[i] = this.isContainPoint(g.points[i]); } for(int item:check2){ if(item != 1) ok = false; } if(this.overlappingArea(g) !=0) ok = false; return ok; } //判斷完全包含另一個圖形(任意點都在this之內) public boolean isContainGra(Graphical g){ boolean ok = true; int[] check2 = new int[g.len]; for(int i=0;i<g.len;i++){ check2[i] = this.isContainPoint(g.points[i]); } for(int item:check2){ if(item == 1) ok = false; } return ok; } //判斷兩個圖形是否一模一樣(點完全重合) public boolean isSameTo(Graphical g){ if(this.len != g.len) return false; for(int i=0;i<this.len;i++){ boolean ok = false; for(int j=0;j<g.len;j++){ if(this.points[i].isSameTo(g.points[j])) ok = true; } if(!ok) return false; } return true; } //計算兩個圖形的重疊面積(交點加內部頂點構成重疊多邊形) public double overlappingArea(Graphical g){ Point[] intersection = new Point[100]; int intersection_len = 0; for(Line item1:this.lines){ //求出兩多邊形的交點 for(Line item2: g.lines){ Point tmp = item1.lsi(item2); if(tmp != null){ intersection[intersection_len++] = tmp.deepCopy(); } } } for(Point item:g.points){ //頂點包含在內部 if(this.isContainPoint(item) == -1) intersection[intersection_len++] = item.deepCopy(); } for(Point item:this.points){ //頂點包含在內部 if(g.isContainPoint(item) == -1) intersection[intersection_len++] = item.deepCopy(); } //if(intersection_len == 0) return 0; //交點為0,分離 //-2分 /*排序交點數組*/ intersection = Arrays.copyOf(intersection,intersection_len); intersection = this.removeMulti(intersection); Point focus = Point.focusPoint(intersection); Point sta = intersection[0].deepCopy(); Arrays.sort(intersection,1,intersection.length, new Comparator<Point>() { @Override public int compare(Point o1, Point o2) { try{ Line origin =new Line(focus,sta); Line l1 = new Line(focus,o1); Line l2 = new Line(focus,o2); double angle1 = origin.vectorAngle(l1); double angle2 = origin.vectorAngle(l2); if(origin.vectorCrossMul(l1) < 0) angle1 = 2*Math.PI - angle1; if(origin.vectorCrossMul(l2) < 0) angle2 = 2*Math.PI - angle2; if(angle1-angle2 > 0.000001) return 1; if(Math.abs(angle1-angle2) < 0.000001) return 0; return -1; }catch (Exception reason){} return 0; } }); Graphical graphical = new Graphical(intersection); return graphical.area; } //去除所有重複點 private Point[] removeMulti(Point[] points){ Point[] tmp_points = new Point[points.length]; int tmp_len = 0; for(int i=0;i<points.length;i++){ boolean ok = true; for(int j=0;j<tmp_len;j++){ if(points[i].isSameTo(tmp_points[j])){ this.message = "points coincide"; ok = false; break; } } if(ok) tmp_points[tmp_len++] = points[i].deepCopy(); } return Arrays.copyOf(tmp_points,tmp_len); } //判斷不相鄰邊是否有交點 private void checkEdge(){ for(int i=0;i<this.len;i++){ for(int j=i+2;j<this.len;j++){ if(i==0&&j==this.len-1) continue; Point p = this.lines[i].getIntersection(this.lines[j]); if(p==null) continue; if(p.inLineSegment_close(this.lines[i]) && p.inLineSegment_close(this.lines[j])){ this.status = -1; this.message = "Non adjacent edges have intersections"; return; } } } } //多邊形面積 private static void area(Graphical e){ double res = 0; Point origin = new Point(0,0); for(int i=0;i<e.len;i++){ try{ Line l1 = new Line(origin,e.points[i]); Line l2 = new Line(origin,e.points[(i+1)%e.len]); res += 0.5 * l1.vectorCrossMul(l2); }catch (Exception reason){} } e.area = Math.abs(res); } //多邊形周長 private static void sideLength(Graphical e){ double res = 0; for(int i=0;i<e.len;i++){ res += e.points[i].disToPoint(e.points[(i+1)%e.len]); } e.sideLength = res; } //多邊形凹凸性 private static void checkConvex(Graphical e){ if(e.len == 3) return; int v = 0; for(int i=0;i<e.len;i++){ int first = i, second = (i+1)%e.len, thrid = (i+2)%e.len; try{ Line l1 = new Line(e.points[first], e.points[second]); Line l2 = new Line(e.points[first], e.points[thrid]); if(v==0){ if(l1.vectorCrossMul(l2) > 0) v = 1; else v = -1; } if(v == 1 && l1.vectorCrossMul(l2) < 0) e.isConvexGraphical = false; if(v == -1 && l1.vectorCrossMul(l2) > 0) e.isConvexGraphical = false; }catch (Exception reason){} } } //是否一樣 }
-
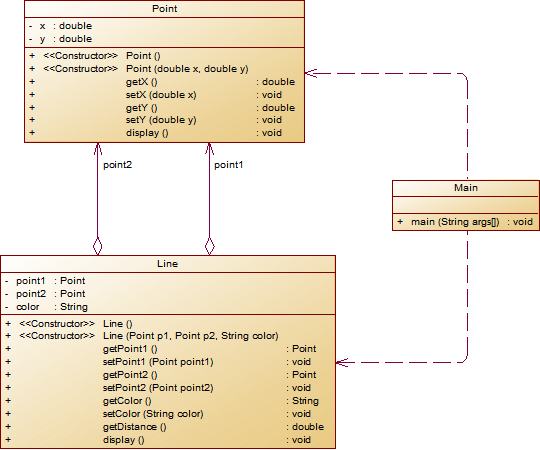
設計一個類表示平面直角坐標繫上的點Point,私有屬性分別為橫坐標x與縱坐標y,數據類型均為實型數,除構造方法以及屬性的getter與setter方法外,定義一個用於顯示資訊的方法display(),用來輸出該坐標點的坐標資訊,格式如下:
(x,y),數值保留兩位小數。為簡化題目,其中,坐標點的取值範圍設定為(0,200]。若輸入有誤,系統則直接輸出Wrong Format -
設計一個類表示平面直角坐標繫上的線Line,私有屬性除了標識線段兩端的點point1、point2外,還有一個字元串類型的color,用於表示該線段的顏色,同樣,除構造方法以及屬性的getter與setter方法外,定義一個用於計算該線段長度的方法getDistance(),還有一個用於顯示資訊的方法display(),用來輸出線段的相關資訊,輸出格式如下:
``` The line's color is:顏色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:長度值 ```其中,所有數值均保留兩位小數,建議可用
String.format("%.2f", data)方法。設計類圖如下圖所示。
** 題目要求:在主方法中定義一條線段對象,從鍵盤輸入該線段的起點坐標與終點坐標以及顏色,然後調用該線段的display()方法進行輸出。**
- 以下情況為無效作業
- 無法運行
- 設計不符合所給類圖要求
- 未通過任何測試點測試
- 判定為抄襲
輸入格式:
分別輸入線段的起點橫坐標、縱坐標、終點的橫坐標、縱坐標以及顏色,中間可用一個或多個空格、tab或者回車分隔。
輸出格式:
The line's color is:顏色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:長度值
輸入樣例1:
在這裡給出一組輸入。例如:
5
9.4
12.3
84
Red
輸出樣例1:
在這裡給出相應的輸出。例如:
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
輸入樣例2:
在這裡給出一組輸入。例如:
80.2356
352.12
24.5
100
Black
輸出樣例2:
在這裡給出相應的輸出。例如:
Wrong Format
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); double x1 = in.nextDouble(); double y1 = in.nextDouble(); double x2 = in.nextDouble(); double y2 = in.nextDouble(); Point a = new Point(x1,y1); Point b = new Point(x2,y2); a.judge(x1,y1); b.judge(x2,y2); String color = in.next(); Line l = new Line(a,b,color); l.display(); } } class Point { private double x; private double y; Point(double x, double y) { this.x = x; this.y = y; } public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } public void display() { System.out.printf("(%.2f,%.2f)", x, y); } public void judge(double x,double y) { if((x<=0||x>200)||(y<=0||y>200)) { System.out.println("Wrong Format"); System.exit(0); } } } class Line{ private Point point1; private Point point2; private String color; private double distance; Line() { } public Line(Point p1, Point p2,String color) { Point p3 = new Point(p1.getX(), p1.getY()); Point p4 = new Point(p2.getX(), p2.getY()); this.point1 = p3; this.point2 = p4; this.color = color; } public void setcolor() { this.color = color; } public String getcolor() { return color; } public double getdistance() { distance = Math.sqrt(Math.abs((point1.getX() - point2.getX())* (point1.getX() - point2.getX())+(point1.getY() - point2.getY())* (point1.getY() - point2.getY()))); this.distance = distance; return distance; } public void display() { double s; s = getdistance(); System.out.println("The line's color is:"+ color); System.out.println("The line's begin point's Coordinate is:"); point1.display(); System.out.println("\nThe line's end point's Coordinate is:"); point2.display(); System.out.printf("\nThe line's length is:%.2f",distance); } }
第一題的總體難度不難,因為一個創建點的時候傳入數據問題導致第一次提交沒有滿分。
在「點與線(類設計)」題目基礎上,對題目的類設計進行重構,以實現繼承與多態的技術性需求。
- 對題目中的點Point類和線Line類進行進一步抽象,定義一個兩個類的共同父類Element(抽象類),將display()方法在該方法中進行聲明(抽象方法),將Point類和Line類作為該類的子類。
- 再定義一個Element類的子類面Plane,該類只有一個私有屬性顏色color,除了構造方法和屬性的getter、setter方法外,display()方法用於輸出面的顏色,輸出格式如下:
The Plane's color is:顏色 - 在主方法內,定義兩個Point(線段的起點和終點)對象、一個Line對象和一個Plane對象,依次從鍵盤輸入兩個Point對象的起點、終點坐標和顏色值(Line對象和Plane對象顏色相同),然後定義一個Element類的引用,分別使用該引用調用以上四個對象的display()方法,從而實現多態特性。示例程式碼如下:
element = p1;//起點Point element.display(); element = p2;//終點Point element.display(); element = line;//線段 element.display(); element = plane;//面 element.display();類結構如下圖所示。
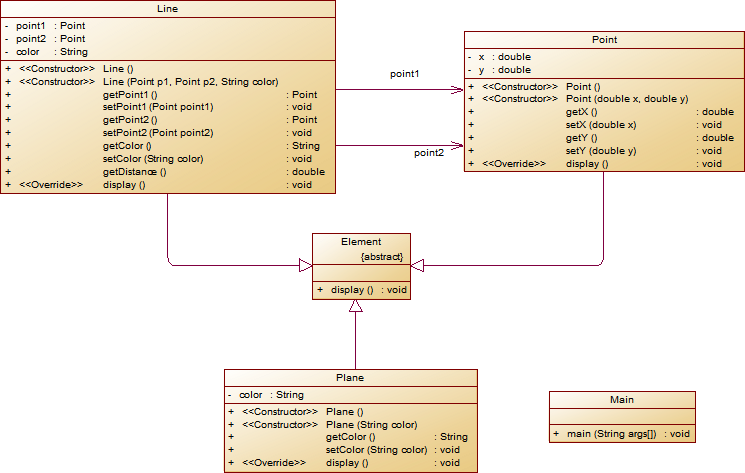
其中,所有數值均保留兩位小數,建議可用String.format("%.2f", data)方法。
- 以下情況為無效作業
- 無法運行
- 設計不符合所給類圖要求
- 未通過任何測試點測試
- 判定為抄襲
輸入格式:
分別輸入線段的起點橫坐標、縱坐標、終點的橫坐標、縱坐標以及顏色,中間可用一個或多個空格、tab或者回車分隔。
輸出格式:
(x1,y1)
(x2,y2)
The line's color is:顏色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:長度值
The Plane's color is:顏色值
輸入樣例1:
在這裡給出一組輸入。例如:
5
9.4
12.3
84
Red
輸出樣例1:
在這裡給出相應的輸出。例如:
(5.00,9.40)
(12.30,84.00)
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
The Plane's color is:Red
輸入樣例2:
在這裡給出一組輸入。例如:
5
9.4
12.3
845
Black
輸出樣例2:
在這裡給出相應的輸出。例如:
Wrong Format
程式碼:
import java.text.DecimalFormat; import java.util.Scanner; public class Main{ public static void main(String[] args){ Scanner in=new Scanner(System.in); Point p1=new Point(); double x1=in.nextDouble(); double y1=in.nextDouble(); double x2=in.nextDouble(); double y2=in.nextDouble(); p1.setX(x1); p1.setY(y1); Point p2=new Point(); p2.setX(x2); p2.setY(y2); String color=in.next(); Line line=new Line(); line.setPoint1(p1); line.setPoint2(p2); line.setColor(color); Plane plane=new Plane(); plane.setColor(color); Element element=new Element() { @Override public void display() { } }; if ((x1<=0||x1>200)||(y1<=0||y1>200)||(x2<=0||x2>200)||(y2<=0||y2>200)) System.out.println("Wrong Format"); else{ element = p1;//起點Point element.display(); element = p2;//終點Point element.display(); element = line;//線段 element.display(); element = plane;//面 element.display(); } } } abstract class Element{ public abstract void display(); } class Point extends Element{ private double x;//橫坐標 private double y;//縱坐標 public Point(double x, double y) { this.x = x; this.y = y; } public Point() { } public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } public void display(){ DecimalFormat two=new DecimalFormat("0.00"); System.out.println("("+two.format(this.x)+","+two.format(this.y)+")"); } } class Line extends Element{ private Point point1 = new Point(); private Point point2 = new Point(); String color; public Line(Point point1, Point point2, String color) { this.point1 = point1; this.point2 = point2; this.color = color; } public Line() { } public Point getPoint1() { return point1; } public void setPoint1(Point point1) { this.point1 = point1; } public Point getPoint2() { return point2; } public void setPoint2(Point point2) { this.point2 = point2; } public String getColor() { return color; } public void setColor(String color) { this.color = color; } public double getDistance(Point p1,Point p2){ double a=p1.getX()-p2.getX(); double b=p1.getY()-p2.getY(); return Math.sqrt(a*a+b*b); } public void display(){ Line line=new Line(); DecimalFormat two=new DecimalFormat("0.00"); System.out.println("The line's color is:"+getColor()); System.out.println("The line's begin point's Coordinate is:"); point1.display(); System.out.println("The line's end point's Coordinate is:"); point2.display(); System.out.println("The line's length is:" + two.format(line.getDistance(point1,point2))); } } class Plane extends Element{ private String color; public Plane(String color) { this.color = color; } public Plane() { } public String getColor() { return color; } public void setColor(String color) { this.color = color; } public void display(){ System.out.println("The Plane's color is:"+this.color); } }
第二題的難度比較適中
在「點與線(繼承與多態)」題目基礎上,對題目的類設計進行重構,增加容器類保存點、線、面對象,並對該容器進行相應增、刪、遍歷操作。
- 在原有類設計的基礎上,增加一個GeometryObject容器類,其屬性為
ArrayList<Element>類型的對象(若不了解泛型,可以不使用<Element>) - 增加該類的
add()方法及remove(int index)方法,其功能分別為向容器中增加對象及刪除第index - 1(ArrayList中index>=0)個對象 - 在主方法中,用戶循環輸入要進行的操作(choice∈[0,4]),其含義如下:
- 1:向容器中增加Point對象
- 2:向容器中增加Line對象
- 3:向容器中增加Plane對象
- 4:刪除容器中第index – 1個數據,若index數據非法,則無視此操作
- 0:輸入結束
示例程式碼如下:
choice = input.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list ... break; case 2://insert Line object into list ... break; case 3://insert Plane object into list ... break; case 4://delete index - 1 object from list int index = input.nextInt(); ... } choice = input.nextInt(); }輸入結束後,按容器中的對象順序分別調用每個對象的
display()方法進行輸出。
類圖如下所示:
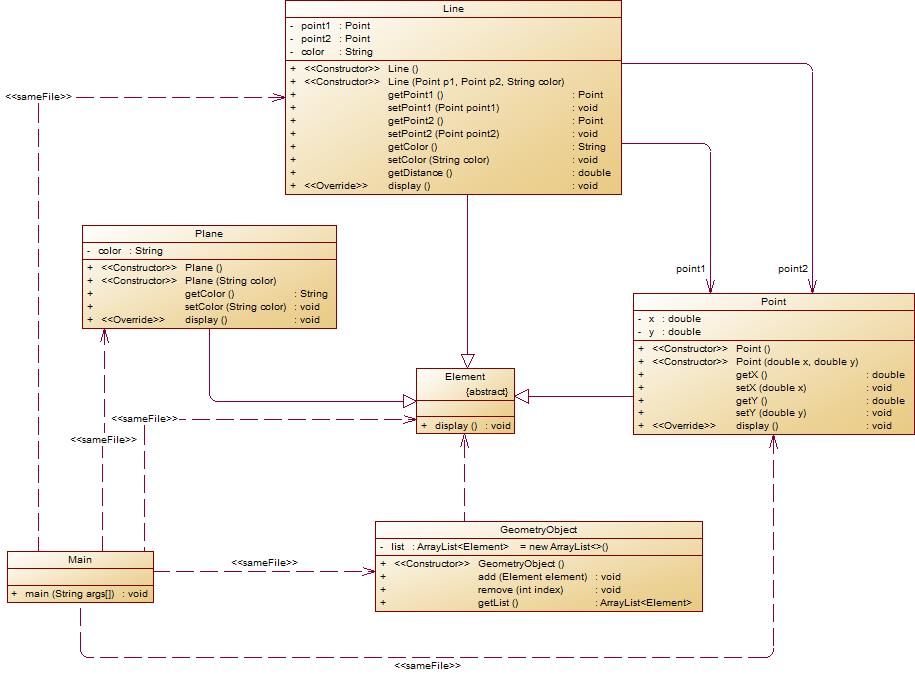
- 以下情況為無效作業
- 無法運行
- 設計不符合所給類圖要求
- 未通過任何測試點測試
- 判定為抄襲
輸入格式:
switch(choice) {
case 1://insert Point object into list
輸入「點」對象的x,y值
break;
case 2://insert Line object into list
輸入「線」對象兩個端點的x,y值
break;
case 3://insert Plane object into list
輸入「面」對象的顏色值
break;
case 4://delete index - 1 object from list
輸入要刪除的對象位置(從1開始)
...
}
輸出格式:
- Point、Line、Plane的輸出參考題目2
- 刪除對象時,若輸入的index超出合法範圍,程式自動忽略該操作
輸入樣例:
在這裡給出一組輸入。例如:
1
3.4
5.6
2
4.4
8.0
0.98
23.888
Red
3
Black
1
9.8
7.5
3
Green
4
3
0
輸出樣例:
在這裡給出相應的輸出。例如:
(3.40,5.60)
The line's color is:Red
The line's begin point's Coordinate is:
(4.40,8.00)
The line's end point's Coordinate is:
(0.98,23.89)
The line's length is:16.25
(9.80,7.50)
The Plane's color is:Green程式碼:
import java.text.DecimalFormat; import java.util.ArrayList; import java.util.Scanner; public class Main{ public static void main(String []args) { Scanner in =new Scanner(System.in); int choice = in.nextInt(); ArrayList<Element> ad = new ArrayList<Element>(); while(choice != 0) { switch(choice) { case 1: Point point1= new Point(in.nextDouble(),in.nextDouble()); ad.add(point1); break; case 2: Point point3= new Point(in.nextDouble(),in.nextDouble()); Point point2= new Point(in.nextDouble(),in.nextDouble()); Line line = new Line(point3,point2,in.next()); ad.add(line); break; case 3: Plane plane=new Plane(in.next()); ad.add(plane); break; case 4: int index = in.nextInt(); ad.remove(index-1); } choice = in.nextInt(); } for (Element element : ad) { element.display(); } } } class Point extends Element{ private double x; private double y; public Point() { } public Point(double x, double y) { super(); this.x = x; this.y = y; } public double getX() { return x; } public void setX(double x) { this.x=x; } public double getY() { return y; } public void setY(double y) { this.y=y; } public void display() { if((x<=0||x>200)||(y<=0)||(y>200)) { System.out.println("Wrong Format"); System.exit(0); }else { System.out.print("("); System.out.printf("%.2f,%.2f",x,y); System.out.println(")"); } } } class Line extends Element{ private Point point1; private Point point2; private String color; public Line() { } public Line(Point point1, Point point2, String color ) { super(); this.point1 = point1; this.point2 = point2; this.color = color; } public Point getPoint1() { return point1; } public void setPoint1(Point point1) { this.point1=point1; } public Point getPoint2() { return point2; } public void setPoint2(Point point2) { this.point2=point2; } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public static double getDistance(Point point1,Point point2) { double a; a=Math.sqrt((point1.getX()-point2.getX())*(point1.getX()-point2.getX())+(point1.getY()-point2.getY())*(point1.getY()-point2.getY())); return a; } public void display() { System.out.println("The line's color is:"+getColor()); System.out.println("The line's begin point's Coordinate is:"); System.out.print("("); System.out.printf("%.2f,%.2f",point1.getX(),point1.getY()); System.out.println(")"); System.out.println("The line's end point's Coordinate is:"); System.out.print("("); System.out.printf("%.2f,%.2f",point2.getX(),point2.getY()); System.out.println(")"); System.out.print("The line's length is:"); System.out.printf("%.2f\n",getDistance(point1,point2)); } } class Plane extends Element{ private String color; public Plane(String color) { super(); this.color = color; } public String getColor() { return color; } public void setColor(String color) { this.color=color; } public void display() { System.out.print("The Plane's color is:"+getColor()); } } class Element{ private double x; private double y; private Point point1; private Point point2; private String color; public void display() { System.out.print("("); System.out.printf("%.2f,%.2f",point1.getX(),point1.getY()); System.out.println(")"); System.out.print("("); System.out.printf("%.2f,%.2f",point2.getX(),point2.getY()); System.out.println(")"); System.out.println("The line's begin point's Coordinate is:"); System.out.print("("); System.out.printf("%.2f,%.2f",point1.getX(),point1.getY()); System.out.println(")"); System.out.println("The line's end point's Coordinate is:"); System.out.print("("); System.out.printf("%.2f,%.2f",point1.getX(),point1.getY()); System.out.println(")"); System.out.print("The line's length is:"); System.out.printf("%.2f",Line.getDistance(point1,point2)); } } class GeometryObject{ ArrayList<Element> ad = new ArrayList<Element>(); public GeometryObject() { super(); } public void add(Element element) { ad.add(element); } public void remove(int index) { if(index>0) ad.remove(index); } public ArrayList<Element> getList(){ return ad; } }
第三個題目沒有全部完成,其實思路還是挺簡單的。
(3)采坑心得:
1.題目集4 7-2 判斷四邊形是否成型時,用了斜率相等判斷平行,但是在樣例中會出現類似分母為零的情況,改用了x1y2=x2y1判斷。
2.考慮相等問題的同時,需要判斷是否需要考慮精度問題,有很多點是沒加精度判斷過不去的,精度不能設置太大也不能太小,合適就好,我的話精度1e-6或者1e-12,具體問題具體分析即可。
3.我們在拿到題目時,不要一股腦的想著如何去實現功能,我們可以先將最終要設計出來的程式碼進行功能分解,進而設計出多個不同功能的類,每個類再根據應有的功能寫出相應的程式碼。
(4)改進建議:對相應題目的編碼改進給出自己的見解,做到可持續改進
1.計算幾何方面知識有所欠缺
2.我們可以參考一下別人程式碼的構造然後去自己模仿著寫,不斷改進自己的程式碼結構。
(5)總結:
這幾次作業極大的提高了本人對面向對象編程的理解,且極大的提高了本人的程式碼能力。我對JAVA中常規類的使用習慣和構建方法更加清楚,可以很熟練地處理三角形、四邊形、五邊形其他類型的題目,也能通過較為合理的設計完成題目要求。


