day53-馬踏棋盤

• 2022 年 10 月 25 日
• 筆記
• JavaSE

馬踏棋盤

1.演算法優化的意義

1. 演算法是程式的靈魂，為什麼有些程式可以在海量數據計算時，依舊保持高速計算？
2. 編程中演算法很多，比如八大排序演算法（冒泡、選擇、插入、快排、歸併、希爾、基數、堆排序）、查找演算法、分治演算法、動態規劃演算法、KMP演算法、貪心演算法、普利姆演算法、克魯斯卡爾演算法、迪傑斯特拉演算法、弗洛伊德演算法
3. 下面以騎士周遊問題為例，體驗演算法優化程式的意義，感受演算法的威力

2.騎士周遊問題

• 馬踏棋盤演算法介紹和遊戲演示

1. 馬踏棋盤演算法也被稱為騎士周遊問題
2. 將馬隨機放在國際象棋的8*8棋盤Board[0-7][0-7]的某個方格中，馬按走棋規則移動（馬只能走日字）。要求每個方格只進入一次，走遍棋盤上全部64個方格
3. 會使用到圖的遍歷演算法（DFS）+貪心演算法優化

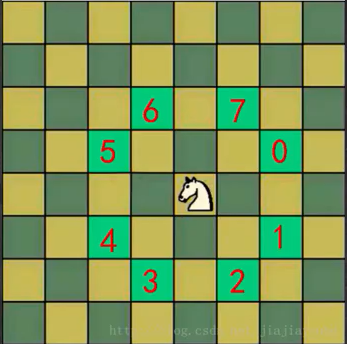
馬踏棋盤(騎士周遊問題)實際上是圖的深度優先搜索(DFS)的應用。

使用回溯(就是深度優先搜索)來解決，假如馬兒踏了53個點，如圖，走到了第53個，坐標為(1,0)，發現已經走到了盡頭，沒辦法，那就只能回退了，查看其它的路徑，就在棋盤上不停地回溯……

這裡我們先用基本的方法解決，然後使用貪心演算法(greedyalgorithm)進行優化。解決馬踏棋盤問題，體會到不同的演算法對程式效率的影響

3.思路分析

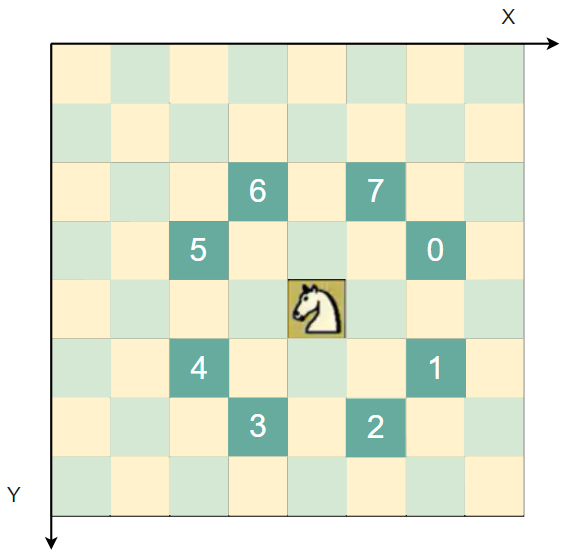
1. 創建一個棋盤chessBoard，是一個二維數組
2. 將馬兒當前位置設置為已經訪問，然後根據當前位置，計算馬兒還能走哪些位置，並放入到一個集合中(ArrayList)，每一個位置的下一步最多有8個方向，每走一步，就使用step+1
3. 遍歷ArrayList中存放的所有位置，看看哪個可以走，如果可以走通，就繼續，走不通，就回溯
4. 判斷馬兒是否完成了任務，使用step和應該走的步數比較，如果沒有達到數量，則表示沒有完成任務，將整個棋盤設置為0

注意：馬兒走的策略不同，得到的結果也會不一樣，效率也不一樣。

package li;

import java.awt.*;
import java.util.ArrayList;

/**
 * @author 李
 * @version 1.0
 * 馬踏棋盤
 */
public class HorseChessBoard {
    //定義屬性
    private static int X = 6;//表示col-列
    private static int Y = 6;//表示row-行
    private static int[][] chessBoard = new int[Y][X];//棋盤
    private static boolean[] visited = new boolean[X * Y];//表示記錄某個位置是否走過
    private static boolean finished = false;//記錄馬兒是否遍歷完棋盤

    public static void main(String[] args) {
        //測試
        int row = 2;
        int col = 2;
        long start = System.currentTimeMillis();
        traversalChessBoard(chessBoard, row-1, col-1, 1);//將棋盤上開始的位置設置為起始第一步
        long end = System.currentTimeMillis();
        System.out.println("遍歷耗時="+(end - start));
        //輸出當前棋盤的情況
        for (int[] rows : chessBoard) {
            for (int step : rows) {//step表示 這個位置是馬兒應該走的第幾步
                System.out.print(step + "\t");
            }
            System.out.println();
        }
    }

    //最核心的演算法，遍歷棋盤，如果遍歷成功，就將finished的值設置為true，
    //並且將馬兒走的每一步step記錄到chessBoard
    public static void traversalChessBoard(int[][] chessBoard, int row, int col, int step) {
        //先將step記錄到chessBoard
        chessBoard[row][col] = step;
        //把這個位置設置為已經訪問
        visited[row * X + col] = true;//就是將二維數組的下標對應到一位數組下標，按行的順序存放（注意下標從0開始）
        //獲取當前位置可以走的下一個位置有哪些
        ArrayList<Point> ps = next(new Point(col, row));//注意col-X,row-Y
        //遍歷
        while (!ps.isEmpty()) {
            //取出當前ps集合的第一個位置（點）
            Point p = ps.remove(0);//每取出一個點，就從集合中刪除這個點
            //判斷該點的位置是否走過，如果沒有走過，就遞歸遍歷
            if (!visited[p.y * X + p.x]) {
                //遞歸遍歷
                traversalChessBoard(chessBoard, p.y, p.x, step + 1);
            }
        }
        //當退出while循環後，看看是否遍歷成功，如果沒有成功，就重置相應的值，然後進行回溯
        if (step < X * Y && !finished) {
            //重置
            chessBoard[row][col] = 0;
            visited[row * X + col] = false;

        } else {
            finished = true;
        }
    }

    //編寫方法，可以獲取當前位置 可以走的下一步 的所有位置(Point表示x,y)
    public static ArrayList<Point> next(Point curPoint) {//curPoint表示當前點
        //先創建一個ArrayList
        ArrayList<Point> ps = new ArrayList<>();

        //創建一個Point對象，表示一個位置/點，準備放入到 ps集合中
        Point p1 = new Point();

        //判斷在curPoint位置，是否可以走如下位置，如果可以走，就將該點(p1)放入到集合ps中
        /**
         * 馬走日的話，每個點就有八個方向可以走，並且這八個方向對於當前坐標的相對坐標都是固定的，
         * 通過當前坐標算出八個方向的相對坐標，然後排除掉那些可能會走出界的方向
         */
        //判斷是否可以走5位置
        if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走6位置
        if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走7位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {//注意索引的範圍是：0到X-1
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走0位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走1位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走2位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走3位置
        if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        //判斷是否可以走4位置
        if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));//要創建一個新的點
        }
        return ps;
    }
}

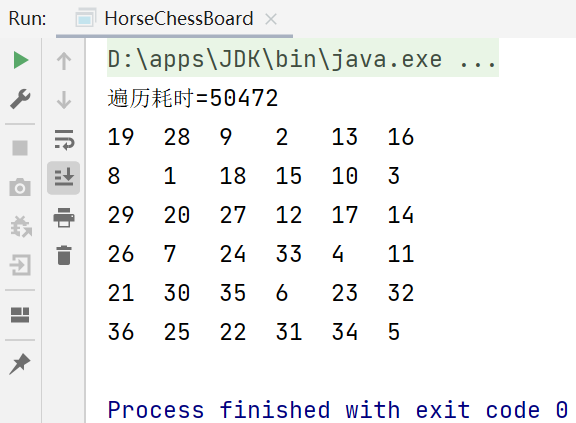
4.優化

1. 根據上面的程式碼，當前點走的下一個位置，是按照我們的順時針方向來挑選位置的，因此，所選擇的點的下一個可以走的位置的個數是不確定的
2. 優化的思路是：我們應該優先選擇的下一個位置，這個位置的再下一個位置應該儘可能少，這樣就可以減少回溯的次數
3. 程式碼：對ps集合按照可以走的下一個位置的次數進行升序排序(從小到大排序)

修改：

1. 編寫方法

//寫一個方法，對ps集合的各個位置，可以走的下一個位置的次數進行排序，把可能走的下一個位置從小到大進行排序
public static void sort(ArrayList<Point> ps){
    ps.sort(new Comparator<Point>() {
        @Override
        public int compare(Point o1, Point o2) {
            return next(o1).size()-next(o2).size();
        }
    });
}

2. 在遞歸中調用該方法，對ps集合按照可以走的下一個位置的次數進行升序排序(從小到大排序)

優化結果：