LeetCode – 二維數組及滾動數組
1. 二維數組及滾動數組總結
在二維數組num[i][j]中,每個元素都是一個數組。有時候,二維數組中的某些元素在整個運算過程中都需要用到;但是有的時候我們只需要用到前一個或者兩個數組,此時我們便可以用幾個數組來代替原來的二維數組來降低空間消耗。這個思維就是:滾動數組。
滾動數組就是使用k個一維數組來保存原來二維數組的後k個數組,在使用的過程中通過不斷更新這k個數組來達到與二維數組相同的效果。
注意:滾動數組的目的是:減少空間消耗;滾動數組能夠使用的前提是:每次處理時不需要訪問二維數組中的所有元素,只與當前處理元素的前一個或兩個數組有關,如:num[i][j] = num[i-1][j] + num[i-2][j]類似情況,我們就可以使用滾動數組。
滾動數組在動態規划過程中經常使用,此處我們先提前了解一下。
2. 題目記錄
118. 楊輝三角
分析題意
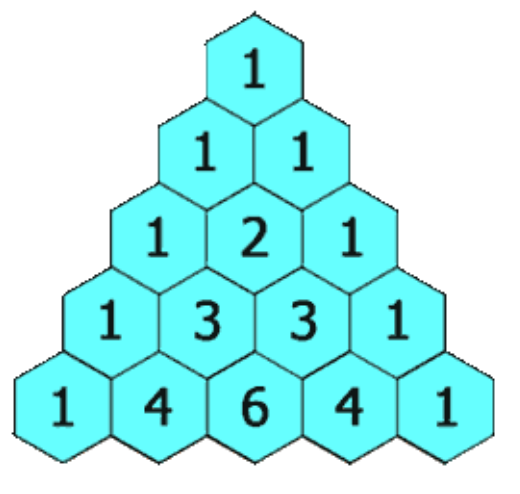
給定一個非負整數 numRows,生成「楊輝三角」的前 numRows行。在「楊輝三角」中,每個數是它左上方和右上方的數的和。
思路分析
關鍵在於理解:楊輝三角是如何生成的。即:對於第i行元素來說,除了第一個和最後一個,對於任意一個元素 j都有nums[i][j] = nums[i-1][j-1] + nums[i-1][j]
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> ans = new ArrayList<>();
for(int row = 1; row <= numRows; row++){
List<Integer> temp = new ArrayList<Integer>();
for(int col = 1; col <= row; col++){
if(col == 1 || col == row){
temp.add(1);
}else{
// row - 1 對應的idx 為 row-1-1
List<Integer> pre = ans.get(row - 2);
// col 對應的idx為col-1
temp.add(pre.get(col-2) + pre.get(col-1));
}
}
ans.add(temp);
}
return ans;
}
}
複雜度分析
時間複雜度:\(O(n^{2})\)
空間複雜度:\(O(1)\) 返回值所佔空間不考慮
119. 楊輝三角 II
分析題意
給定一個非負索引 rowIndex,返回「楊輝三角」的第 rowIndex 行。在「楊輝三角」中,每個數是它左上方和右上方的數的和。
思路分析
這個題和上一道題很相似,區別在於:本題只需要返回指定行的結果。根據題意知道,第i行的數據只與第i-1行的數據有關係,所以我們可以使用滾動數組來將二維數組壓縮為兩個數組。
class Solution {
public List<Integer> getRow(int rowIndex) {
int[] pre = new int[rowIndex + 1];
int[] cur = new int[rowIndex + 1];
for(int idx = 0; idx <= rowIndex; idx++){
for(int j = 0; j < idx + 1; j++){
if(j == 0 || j == idx){
cur[j] = 1;
}else{
cur[j] = pre[j-1] + pre[j];
}
}
int[] temp = pre;
pre = cur;
cur = temp;
}
List<Integer> ans = new ArrayList<>();
for(int i = 0; i < pre.length; i++){
ans.add(pre[i]);
}
return ans;
}
}
複雜度分析
時間複雜度:\(O(n^2)\)
空間複雜度:\(O(n)\),通過滾動數組,我們將空間消耗從\(O(n^{2})\)降為了\(O(n)\)。
擴展
其實這道題可以繼續優化,如果不考慮返回數據佔用的空間,這道題可以做到O(1)的空間複雜度。
做到O(1)空間複雜度的思路就是:將上述兩個數組合併為一個數組,關鍵問題就是怎麼才能復用這個數組呢?
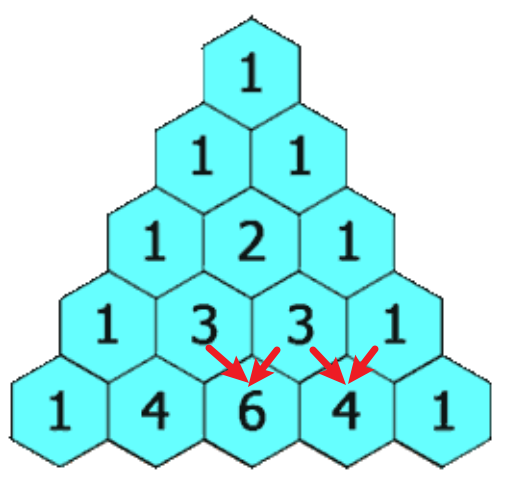
我們直接創建一個大小為n的ans數組,假定我們想要第4行的數據,而我們已經遍歷過第3行,那麼此時ans數組中的元素為:
[1, 3, 3, 1, 0]
如果我們從前到後遍歷,那麼在遍歷到j=2時,數組被更新為:
[1, 4, 3, 1, 0]
那麼此時計算j=3時,j=2位置的元素已經被覆蓋為第4行的新數據,而不是第3行的舊數據。所以我們不能從做左到右進行遍歷。我們再思考一下,第j個元素的更新依賴於j-1和j元素,只更新j元素,所以我們可以從後向前遍歷!
從後向前遍歷防止之前元素被覆蓋的思路在背包問題中也有體現。
class Solution {
public List<Integer> getRow(int rowIndex) {
List<Integer> ans = new ArrayList<>();
for(int i = 0; i <= rowIndex; i++){
ans.add(1);
}
for(int idx = 2; idx <= rowIndex; idx++){
// 從後往前遍歷,防止前一層的元素被覆蓋掉
for(int j = idx; j >=0; j--){
if(j == idx || j == 0){
// 第idx行的第1個和最後1個元素為1,不需要修改
continue;
}else{
ans.set(j, ans.get(j) + ans.get(j-1));
}
}
}
return ans;
}
}
661. 圖片平滑器
分析題意
注意:3x3滑動窗內的9個數字的平均值,需要向下取整。還需要注意的一點就是:如果個數小於9個,那麼求平均值的時候應該除以真正的數字的數目,而不是除以9。
思路分析
按照題意進行滑動窗的模擬操作。
對於(i, j)坐標,它周圍的8個坐標分布如下:
(i-1, j-1) (i-1, j) (i-1, j+1)
(i, j-1) (i, j) (i, j+1)
(i+1, j-1) (i+1, j) (i+1, j+1)
class Solution {
public int[][] imageSmoother(int[][] img) {
int[][] ans = new int[img.length][img[0].length];
for(int i = 0; i < img.length; i++){
for(int j = 0; j < img[0].length; j++){
ans[i][j] = getAverage(img, i, j);
}
}
return ans;
}
int getAverage(int[][] img, int i, int j){
int sum = 0;
int num = 0;
// i - 1 層
if(i - 1 >= 0){
if(j - 1 >= 0){
sum += img[i-1][j-1];
num++;
}
sum += img[i-1][j];
num++;
if(j + 1 < img[0].length){
sum += img[i-1][j+1];
num++;
}
}
if(j - 1 >= 0){
sum += img[i][j-1];
num++;
}
sum += img[i][j];
num++;
if(j + 1 < img[0].length){
sum += img[i][j + 1];
num ++;
}
// i + 1 層
if(i + 1 < img.length){
if(j - 1 >= 0){
sum += img[i + 1][j - 1];
num ++;
}
sum += img[i + 1][j];
num ++;
if(j + 1 < img[0].length){
sum += img[i + 1][j + 1];
num ++;
}
}
return sum / num;
}
}
簡化的程式碼如下:
class Solution {
int[] row = {-1, -1, -1, 0, 0, 0, 1, 1, 1};
int[] col = {-1, 0, 1, -1, 0, 1, -1, 0, 1};
public int[][] imageSmoother(int[][] img) {
int[][] ans = new int[img.length][img[0].length];
for(int i = 0; i < img.length; i++){
for(int j = 0; j < img[0].length; j++){
ans[i][j] = getAverage(img, i, j);
}
}
return ans;
}
int getAverage(int[][] img, int i, int j){
int sum = 0;
int num = 0;
for(int idx = 0; idx < 9; idx++){
// 判斷坐標是否合法
if(i + row[idx] >= 0 && i + row[idx] < img.length && j + col[idx] >= 0 && j + col[idx] < img[0].length){
sum += img[i + row[idx]][j + col[idx]];
num ++;
}
}
return sum / num;
}
}
複雜度分析
時間複雜度:\(O(n^2)\)
空間複雜度:\(O(1)\) 返回數組佔用空間不計入
598. 範圍求和 II
分析題意
注意關鍵詞:初始化時所有的 0 ,也就是說所有數值在操作之前都是0。
思路分析
這道題看似是需要創建一個二維數組,然後一次一次模擬操作,最後遍歷查出最大的數據的個數。其實,並不需要這樣。我們想一下:因為二維數組初始化時都是0,所以在所有操作完成之後,二維數組中每個單元格內的數字其實就是有多少個操作包含了這個單元格。又因為所有操作都是從(0, 0)開始的,所以我們要求最大的整數出現的頻次,那其實就是求:所有操作的的最小交集。
class Solution {
public int maxCount(int m, int n, int[][] ops) {
int a = m;
int b = n;
for(int i = 0; i < ops.length; i++){
a = Math.min(a, ops[i][0]);
b = Math.min(b, ops[i][1]);
}
return a * b;
}
}
複雜度分析
時間複雜度:\(O(n)\)
空間複雜度:\(O(1)\)
419. 甲板上的戰艦
分析題意
這道題就是一道語文題,能不能做出來完全取決於你有沒有理解題目在說什麼。
首先,明確一個:題目是要統計board上的軍艦數量,而不是要你計算軍艦的數量。我第一次做的時候就是以為要模擬計算軍艦的數量,所以一直沒有做出來。
其次,要明確戰艦的定義,戰艦或者是橫著擺放或者是豎著擺放。也就是說一個戰艦,他要麼佔一行的很多列,要麼站一列的很多行;不可能同時佔用很多行和很多列。
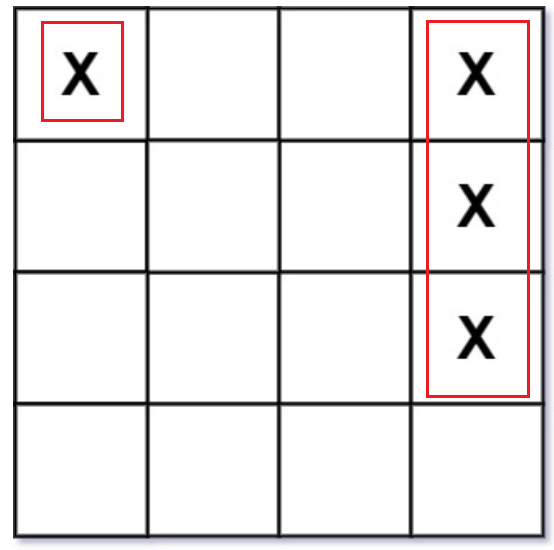
上述兩個紅框就是兩個戰艦,所以此時答案為2。
思路分析
其實我們只需要找到戰艦的頭就可以了,那麼戰艦的頭怎麼尋找呢?其實就是它的左側和上側都沒有戰艦,那麼這個戰艦一定是戰艦頭部。
class Solution {
public int countBattleships(char[][] board) {
int ans = 0;
for(int i = 0; i < board.length; i++){
for(int j = 0; j < board[0].length; j++){
// 此處有戰艦
if(board[i][j] == 'X'){
boolean flag = true;
if(i - 1 >= 0 && board[i-1][j] != '.'){
flag = false;
}
if(j - 1 >= 0 && board[i][j-1] != '.'){
flag = false;
}
if(flag){
ans++;
}
}
}
}
return ans;
}
}
複雜度分析
時間複雜度:\(O(m \times n)\)
空間複雜度:\(O(1)\)

