樹的基本概念介紹

• 2022 年 9 月 21 日
• 筆記
• 數據結構和演算法

為什麼需要樹這種數據結構

這是我本人在B站看韓順平老師數據結構和演算法的學習筆記，記錄一下，防止忘記

1) 數組存儲方式的分析

優點：通過下標方式訪問元素，速度快。對於有序數組，還可使用二分查找提高檢索速度。

缺點：如果要檢索具體某個值，或者插入值(按一定順序)會整體移動，效率較低 [示意圖]

畫出操作示意圖：

2) 鏈式存儲方式的分析

優點：在一定程度上對數組存儲方式有優化(比如：插入一個數值節點，只需要將插入節點，鏈接到鏈表中即可，

刪除效率也很好)。

缺點：在進行檢索時，效率仍然較低，比如(檢索某個值，需要從頭節點開始遍歷) 【示意圖】

3) 樹存儲方式的分析

能提高數據存儲，讀取的效率, 比如利用 二叉排序樹(Binary Sort Tree)，既可以保證數據的檢索速度，同時也 可以保證數據的插入，刪除，修改的速度。【示意圖】

案例: [7, 3, 10, 1, 5, 9, 12]

樹的示意圖

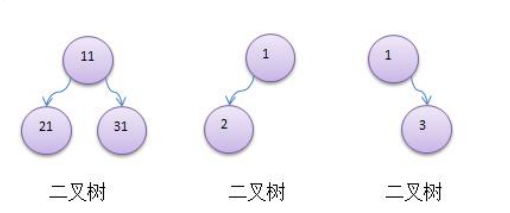
1. 樹有很多種，每個節點最多只能有兩個子節點的一種形式稱為二叉樹。

2. 二叉樹的子節點分為左節點和右節點

3. 示意圖
   

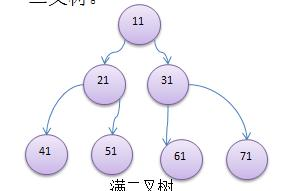
4. 如果該二叉樹的所有葉子節點都在最後一層，並且結點總數= 2^n -1 , n 為層數，則我們稱為滿二叉樹
   

5. 如果該二叉樹的所有葉子節點都在最後一層或者倒數第二層，而且最後一層的葉子節點在左邊連續，倒數第二
   層的葉子節點在右邊連續，我們稱為完全二叉樹
   

二叉樹遍歷的說明

使用前序，中序和後序對下面的二叉樹進行遍歷.

1. 前序遍歷: 先輸出父節點，再遍歷左子樹和右子樹

2. 中序遍歷: 先遍歷左子樹，再輸出父節點，再遍歷右子樹

3. 後序遍歷: 先遍歷左子樹，再遍歷右子樹，最後輸出父節點

4. 小結: 看輸出父節點的順序，就確定是前序，中序還是後序