損失函數里一般有兩種參數，一種是控制輸入訊號量的權重(Weight, 簡稱$ w $），另一種是調整函數與真實值距離的偏差（Bias，簡稱$ b $），在這裡我們將參數統一表示為$ \theta_t \in R^{d} $，損失函數為$J(\theta)$，學習率為$\eta$ 。損失函數關於當前參數的梯度：$g_t = \nabla J(\theta_t)$

損失函數用來衡量機器學習模型的精確度。一般來說，損失函數的值越小，模型的精確度就越高。想要使損失函數最小化，就要用到梯度的概念。梯度是指向變化最快的方向。知道了該往哪裡走，接下來就是該走多長，這用學習率$\eta$來控制

【1】梯度下降

參數更新公式：$\theta_{t+1} = \theta_t – g_t $
原始梯度下降法在迭代每一次梯度下降的過程中，都對所有樣本數據的梯度進行計算，理論上可以找到全局最優解。雖然最終得到的梯度下降的方向較為準確，但是運算會耗費過長的時間。兩種改進方法為：
1.小批量樣本梯度下降（Mini Batch GD)
小批量的意思就是演算法在每次梯度下降的過程中，只選取一部分的樣本數據進行計算梯度，可以明顯地減少梯度計算的時間。
2. 隨機梯度下降（Stochastic GD)
隨機梯度下降演算法只隨機抽取一個樣本進行梯度計算，每次都是往局部最優的方向下降，由於每次梯度下降迭代只計算一個樣本的梯度，因此運算時間比小批量樣本梯度下降演算法還要少很多，但由於訓練的數據量太小（只有一個），因此下降路徑很容易受到訓練數據自身噪音的影響。（只選取一個樣本求梯度也能基本收斂的原因好像和期望有關）。

隨著每次傳入樣本的不同，計算得到的梯度也會不同，這就造成了偏差，所以Mini Batch和SGD都不可避免會發生震蕩

雖然梯度是指向變化最快的方向，但還是有優化空間的，主要是因為我們算的是每個點的梯度，而我們梯度的步長並不是無限小。而有了這個確定的步長，下降路徑就不會和最優路徑重合。

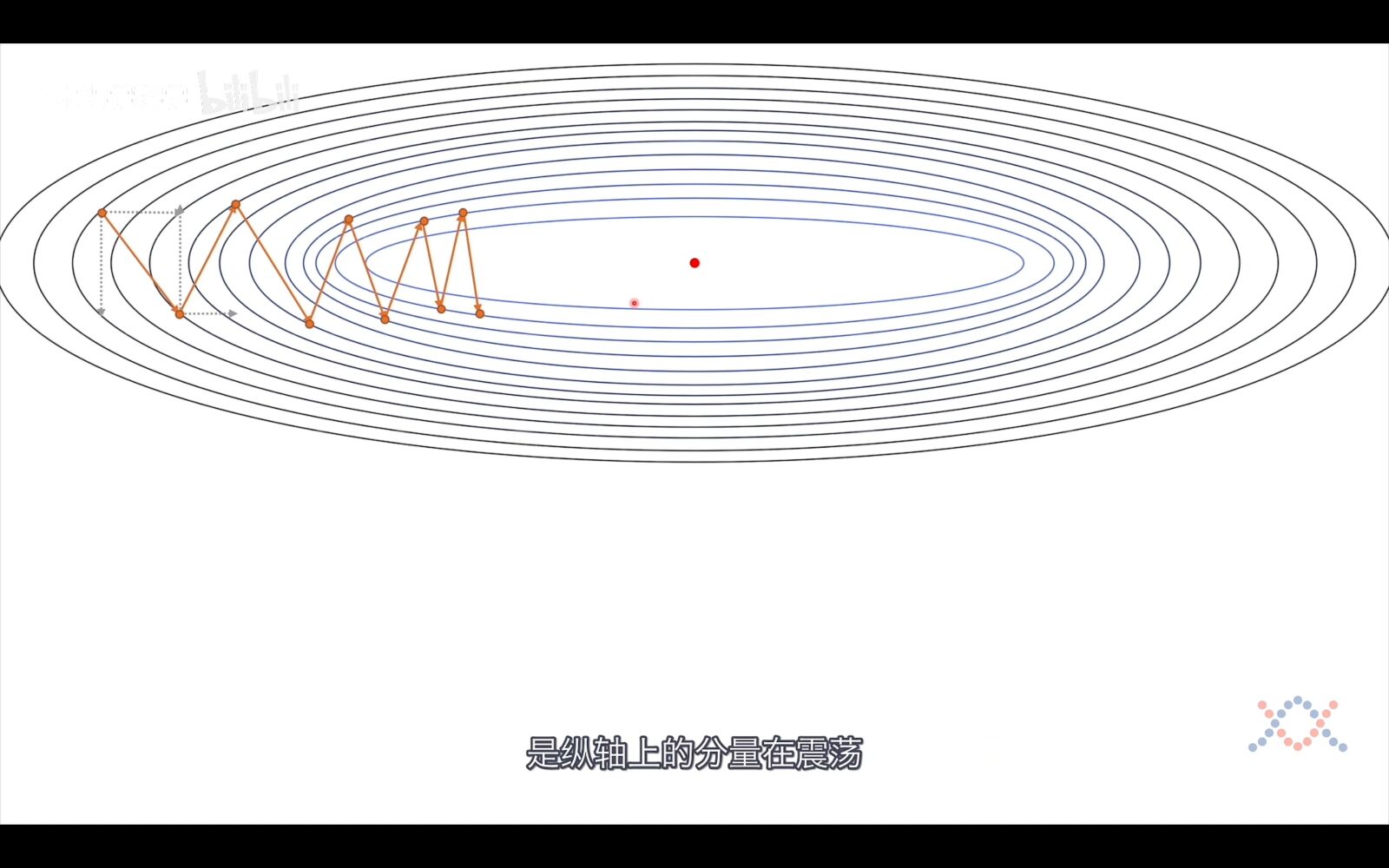
從上圖我們可以看到，梯度的下降過程是震蕩的，一次梯度的下降是橫向向量和縱向向量的和，我們的目的是使梯度指向最優點的方向並增加步長，而這可以通過將橫向向量變長，縱向向量變短來實現，而考慮到向量是有方向的，在垂直方向上，前後兩個向量是反向的，相加後就可以實現縱向向量變短的目的，在水平方向上，前後兩個向量是同向的，相加後就可以實現橫向向量的變長，這正是接下來介紹的動量法的思想，將歷史資訊考慮進去。

【2】Momentum–動量法

Momentum認為梯度下降過程可以加入慣性，就是將歷史梯度考慮進來：
參數更新公式如下：
$m_{t+1} = \beta m_t + \eta g_t $
$\theta_{t+1} = \theta_t – m_{t+1} $
如果將$m_{t+1} $寫開來就是：$m_{t+1} = \eta\sum_{i=1}^t g_t $
此時$\theta_{t+1} = \theta_t -\eta\sum_{i=1}^t g_t $

【3】Nesterov Accelerated Gradient

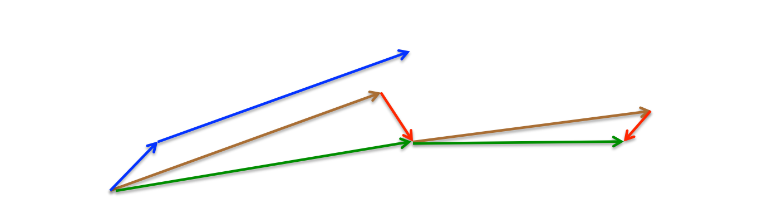
上述圖片來自論文《An overview of gradient descent optimization algorithms》
Momentum首先計算當前的梯度（圖3中的藍色小矢量），然後向更新的累積梯度（藍色大矢量）方向大跳，而NAG首先向之前的累積梯度（棕色矢量）方向大跳，測量梯度，然後進行校正（綠色矢量）。這種預見性的更新可以防止我們走得太快，並導致反應能力的提高。
在Momentum的基礎上將當前時刻的梯度$g_t$換成下一時刻的梯度$\nabla J(\theta_t – \beta m_{t-1})$
參數更新公式為：
$m_{t+1} = \beta m_t + \eta\nabla J(\theta_t – \beta m_{t-1}) $
$\theta_{t+1} = \theta_t – m_{t+1} $

【4】AdaGrad（Adaptive gradient algorithm 自適學習率應梯度下降）

Adagrad 演算法解決的問題：演算法不能根據參數的重要性而對不同的參數進行不同程度的更新的問題。
SGD及其變種均以同樣的學習率更新每個緯度的參數，但深度神經網路往往包含大量的參數，這些參數並不是總會用得到。對於經常更新的參數，我們已經積累了大量關於它的只是，不希望受到單個樣本太大的影響，希望學習速率慢一些；對於偶爾更新的參數，我們了解的資訊太少，希望能從每個偶然出現的樣本身上多學一些，即學習速率大一些。因此，AdaGrad誕生了，它就是考慮了對不同維度的參數採用不同的學習率。

以前，一次性對所有參數$\theta$ 進行更新，因為每個參數$\theta_i $ 都使用相同的學習率$\eta$ 。由於Adagrad在每個時間步驟$t$對每個參數$\theta_i $使用不同的學習率，我們首先展示Adagrad的每個參數更新，然後將其矢量化。為簡潔起見，定義$g_{t,i}$為目標函數的梯度，即在時間步長$t$時對參數$\theta_i $的梯度。

參數更新公式：
$ v_{t,i} = \sum_{i=1}^t{g_{t,i}^2} $
$V_t = diag(v_{t,1},v_{t,2},\cdots,v_{t,d}\in R^{d \times d}) $
$ \theta_{t+1} = \theta_t – \frac{\eta}{\sqrt V_t+\epsilon} $

另一種公式表示：

$ E[g^2]_t=E[g^2]_{t-1}+g_t^2$
$\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{E[g^2]_t+\epsilon}}\times g_t$

特點：前期：較小的時候，分母較大，能夠放大梯度。後期：較大的時候，分母較小，能夠約束梯度。適合處理稀疏梯度 \\
缺點：因為所有梯度一直是累加的，故學習率會一直減小趨於0

【5】RMSprop

RMSprop和下一個提到的優化器都是要解決Adagrad的缺點提出的改進演算法，既然Adagrad的缺點是梯度平方的累加，那我們就減少累加的梯度，具體使用指數衰減移動平均演算法來實現。

參數更新：
$ v_{t,i} = \beta v_{t-1,i} + (1-\beta)g_{t,i}^2 $
$V_t = diag(v_{t,1},v_{t,2},\cdots,v_{t,d}\in R^{d \times d}) $
$ \theta_{t+1} = \theta_t – \frac{\eta}{\sqrt V_t+\epsilon} $

另一種公式表示：

$ E[g^2]_t=\beta E[g^2]_{t-1}+(1-\beta)g_t^2$
$\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{E[g^2]_t+\epsilon}}\times g_t$

【6】Adadelta

RMSprop優化器雖然可以對不同的權重參數自適應的改變學習率，但仍要指定超參數$\eta$，AdaDelta優化器對RMSProp演算法進一步優化：AdaDelta演算法額外維護一個狀態變數$\delta x_t$，並使用$RMS[\delta x]_t$代替RMSprop中的學習率參數$\eta$，使AdaDelta優化器不需要指定超參數.
參數更新公式：
$ E[g^2]_t = \beta E[g^2]_{t-1} + (1-\beta )g_t^2 $ \ 註：符號$E[]$表示期望
$E[\Delta x^2]_{t-1}=\beta \times E[\Delta x^2]_{t-2}+(1-\beta)\times \Delta x_{t-2}^2$
$RMS[g]_t=\sqrt{E[g^2]_t+\epsilon}$
$RMS[\Delta x]_{t-1}=\sqrt{E[\Delta x^2]_{t-1}+\epsilon}$
$\theta_{t+1} = \theta_t – \frac {RMS[\Delta x]_{t-1}}{RMS[g]_t} \otimes g_t$

【7】Adam

$ m_t = \beta_1 m_{t-1}+(1-\beta_1)g_t $
$ v_t = \beta_2 v_{t-1}+(1-\beta_2)g_t^2 $
$ \hat m_t = \frac{m_t}{1-\beta_1^t} $
$ \hat v_t = \frac{v_t}{1-\beta_2^t} $
$ \theta_{t+1} = \theta_t – \frac{\eta}{\sqrt{\hat v_t} +\epsilon} \hat m_t $

【8】AdaMaX

$ m_t = \beta_1 m_{t-1}+(1-\beta_1)g_t $
$ \begin{equation}\begin{split} u_t &= \beta_2^{\infty}v_{t-1} + (1-\beta_2^\infty)\vert g_t \vert^\infty \\ &=max(\beta_2 \cdot v_{t-1},\vert g_t \vert) \end{split}\end{equation} $
$ \theta_{t+1}=\theta_t – \frac{\eta}{u_t}\hat m_t $

【9】Nadam