【題解筆記】PTA基礎6-10:階乘計算升級版
題目地址://pintia.cn/problem-sets/14/problems/742
前言
咱目前還只能說是個小白,寫題解是為了後面自己能夠回顧。如果有哪些寫錯的/能優化的地方,也請各位多指教。( •̀ ω •́ )
題目描述
本題要求實現一個列印非負整數階乘的函數,要求能處理一定大數值的階乘。
展開查看詳情
函數介面定義
void Print_Factorial ( const int N );
其中N是用戶傳入的參數,其值不超過1000。如果N是非負整數,則該函數必須在一行中列印出N!的值,否則列印"Invalid input"。
裁判測試程式樣例
#include <stdio.h>
void Print_Factorial ( const int N );
int main()
{
int N;
scanf("%d", &N);
Print_Factorial(N);
return 0;
}
/* 你的程式碼將被嵌在這裡 */
輸入樣例
15
輸出樣例
1307674368000
限制
| 限制內容 | 限制條件 |
|---|---|
| 程式碼長度限制 | 16 KB |
| 時間限制 | 400 ms |
| 空間限制 | 64 MB |
想法
怎麼儲存如此之大的階乘結果
不看不知道,細看嚇一跳,題目中對N的限制是0<=N<=1000,得想個辦法讓程式儲存1000!這麼大的一個數。
掃視了一圈C語言的基本數據類型,就連unsigned long long類型也遠存不下1000的階乘。
轉換一下思路。數字每一位之間都是緊挨在一起的,我們其實可以採用一種連續的數據結構來儲存這個結果,比如….數組!
設數組第一個元素表示個位,第二個元素表示十位…以此類推。這樣一來,我們就可以用數組以數位升序來儲存這個大數了。最後只需將數組中的每個元素(int)列印到螢幕上即可。
給數組分配多少個元素
題目的裁判測試程式並沒有引入stdlib.h頭文件,因此我沒法使用動態記憶體分配/回收函數。而1000!的結果到底有多少位,我一時半會兒也是不知道的。
其實可以用最簡單粗暴的方式估計一下:1000個1000相乘
\]
這樣算出來的結果有3001位。如果是運算1000!的話,是怎麼也不會算出3001個數位的數字的,所以分配3000個元素一定能保證數組能裝得下結果的所有數位。
註:有一種可以用來計算階乘近似值的公式——斯特林公式
實現乘法時關注的對象
階乘運算的基礎是乘法運算,只要把正確的乘法演算法寫出來,這道題咱們就幾乎能解決了!
關於乘法演算法,我覺得要關注以下三種情況:
-
無需進行進位操作
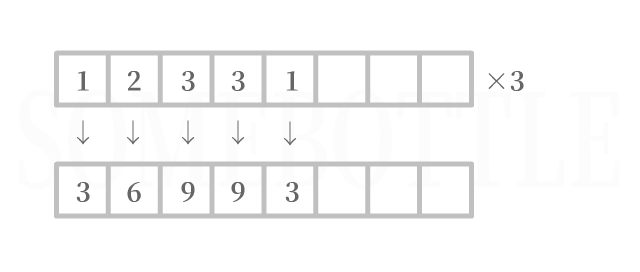
每一位數字乘上因數後均未超過
9,無需進位。 -
需要進行進位操作
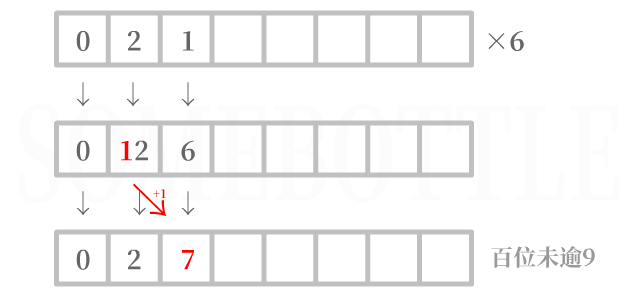
假設當前處理的是十位,十位數字乘上因數後為
12,超過了9。將12「拆成」1和2,將最低位2保留下來,其餘的數位1進入高位。
-
需要進行進位操作,而且進了一位後的數位又可以再進一位
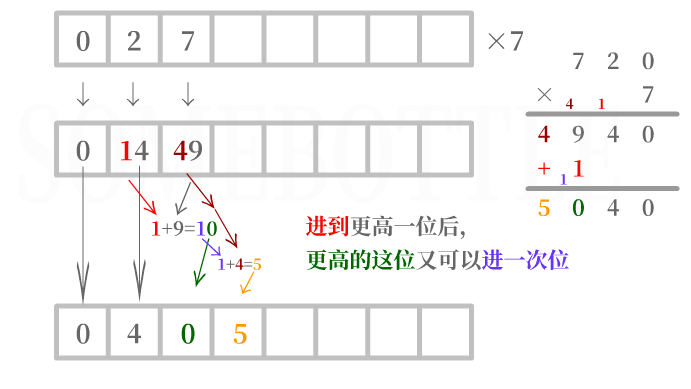
假設當前處理的是百位,百位數字乘上因數後為
49,超過了9。將49「拆成」4和9,將最低位9保留下來,其餘的數位4進入高位。然而此時發現,之前在處理十位時,十位上的數字被拆分為
1和4,其中1進入到百位,而百位現在的數字是9,9+1又可以向後進一位。9+1=10,因此將0保留下來,而1進入高位,加上之前進入高位的數字4,現在進入高位的數字是4+1=5。註:這是很容易被忽略的一種情況。
根據以上描述,可以發現在每次迭代中,我關注的是:
- 當前處理的數位
- 進入到下一位的數值
處理乘法中的進位
上面給出的演示中,進入高位的數字都沒有超過9,那麼如果要進入高位的數字超過了9怎麼辦呢?
實際上這裡和上面的處理方法是差不多的。
每次迭代中處理進到當前數位的數值時,將待進位的數值中的最低位進到當前的數位,在去除待進位的數值中的最低位後,剩餘的數值留到後面處理更高位的進位。
咱做了一個動圖來直觀地演示一下這個過程:
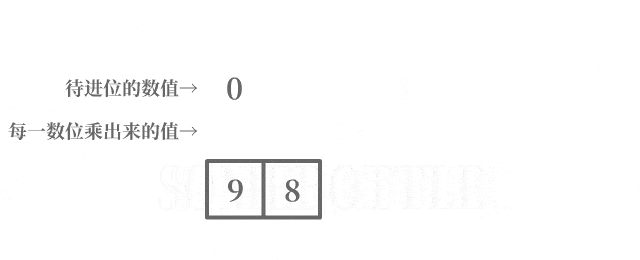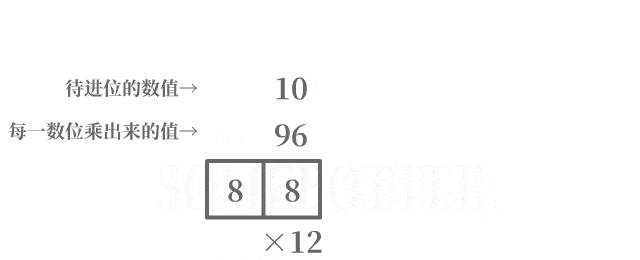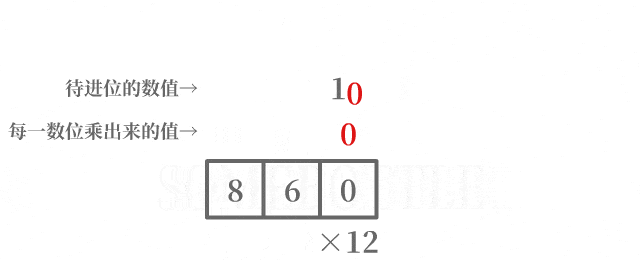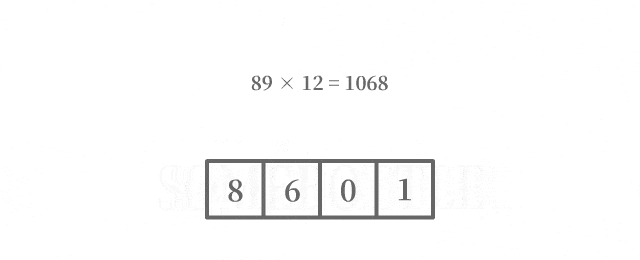
程式碼實現乘法部分
這裡只截取了乘法部分,完整程式碼可以看下方題解程式碼
// arr是按數位儲存結果的數組
// arrLen是上述數組的長度,也代表了結果數值的位數
// factor是每次迭代中要乘上的因數
// 將數組每一位都乘i,並進行進位處理(超過9的數字往高處進)
int j;
int carry = 0; // 要進到高位的數字
int multiplied; // 用於臨時儲存數組中每一位數字乘了因數之後的值
int calcDigit; // 用於臨時儲存新計算出來的某一個數位
for (j = 0; j < arrLen; j++) {
multiplied = arr[j] * factor; // 每一位都乘i
// multiplied % 10 取 <當前數位×因數> 的最低位,比如6*3=18>9,這個時候取出8,而1要進到高位
// carry % 10 將 <上一次迭代留給本次迭代進位的數值> 的最低位取出,這一位是進到 <當前正在處理的數位> 的
calcDigit = multiplied % 10 + carry % 10;
// 運算留給 <下一次迭代> 進位的數值(carry)
// 將 <進到當前數位的值> 去掉最低位(因為最低位在上面已經進到當前數位了),加上multiplied要進到高位的數字
carry = carry / 10 + multiplied / 10;
// 一種很容易錯的情況,雖然multiplied % 10和carry % 10分別不會>=10,但是他們加起來是可能>=10的!
// 也就是說,當前處理的數位在進位後可能>=10,需要再處理一道
// 這種時候還要再進一次位
if (calcDigit >= 10) {
// 將除最低位外的數位加到 <下一次迭代> 進位的數值(carry)上
carry += calcDigit / 10;
// 當前數位只保留最低位
calcDigit %= 10;
}
// 存入最終運算出來的當前數位的值
arr[j] = calcDigit;
// j到數組邊界了,但是還有要進到高位的數值,這說明位數不夠了,那麼就增加位數(增加數組元素)
if (j >= arrLen - 1 && carry > 0)
arrLen++;
}
題解程式碼
部分正確
這部分正確的程式碼錯就錯在忽略了當前數位的二次進位問題。
展開查看詳情
void Print_Factorial(const int N) {
if (N < 0) {
printf("Invalid input");
return;
}
int arr[3000] = {};
arr[0] = 1;
int arrLen = 1;
int factor = 2;
for (; factor <= N; factor++) {
int j;
int carry = 0;
int multiplied;
for (j = 0; j < arrLen; j++) {
multiplied = arr[j] * factor;
arr[j] = multiplied % 10 + carry % 10;
carry = carry / 10 + multiplied / 10;
// 這裡少考慮了一種情況
if (j >= arrLen - 1 && carry > 0)
arrLen++;
}
}
int i;
for (i = arrLen - 1; i >= 0; i--) {
printf("%d", arr[i]);
}
}
Accepted
void Print_Factorial(const int N) {
if (N < 0 || N > 1000) {
printf("Invalid input");
return;
}
/*
如果階乘結果大到C語言中任意一種基本數據類型都無法表達,
不妨考慮一下能不能用某種數據結構來解決問題
這裡採用數組
*/
/* 1000個1000相乘:1*(10^(3*1000))=1e+3000,
結果是1000000000....(3000個零)
而本題N不超過1000,階乘結果肯定也達不到1e+3000,
這裡就給數組分配3000個元素
*/
// 從數組第一個元素為個位開始,往後數位升高
int arr[3000] = {}; // 全初始化為0
arr[0] = 1; // 個位為1
int arrLen = 1; // 標記數組目前元素個數(結果位數)
int factor = 2; // 從2開始乘,因為arr[0]=1
for (; factor <= N; factor++) {
int j;
int carry = 0;
int multiplied;
int calcDigit;
for (j = 0; j < arrLen; j++) {
multiplied = arr[j] * factor;
calcDigit = multiplied % 10 + carry % 10;
carry = carry / 10 + multiplied / 10;
if (calcDigit >= 10) {
carry += calcDigit / 10;
calcDigit %= 10;
}
arr[j] = calcDigit;
if (j >= arrLen - 1 && carry > 0)
arrLen++;
}
}
// 列印結果數字
int i;
// 因為隨著下標增加,數位升高,要列印出來正常的數值就得倒著遍曆數組
for (i = arrLen - 1; i >= 0; i--) {
printf("%d", arr[i]);
}
}
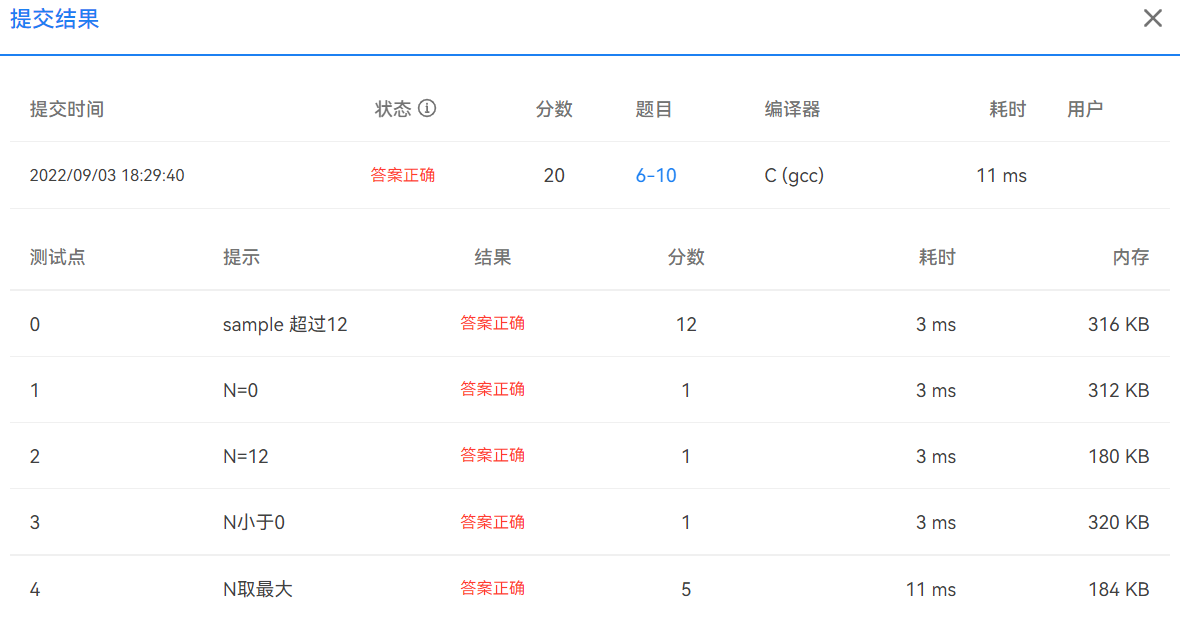
提交結果截圖
-
WA
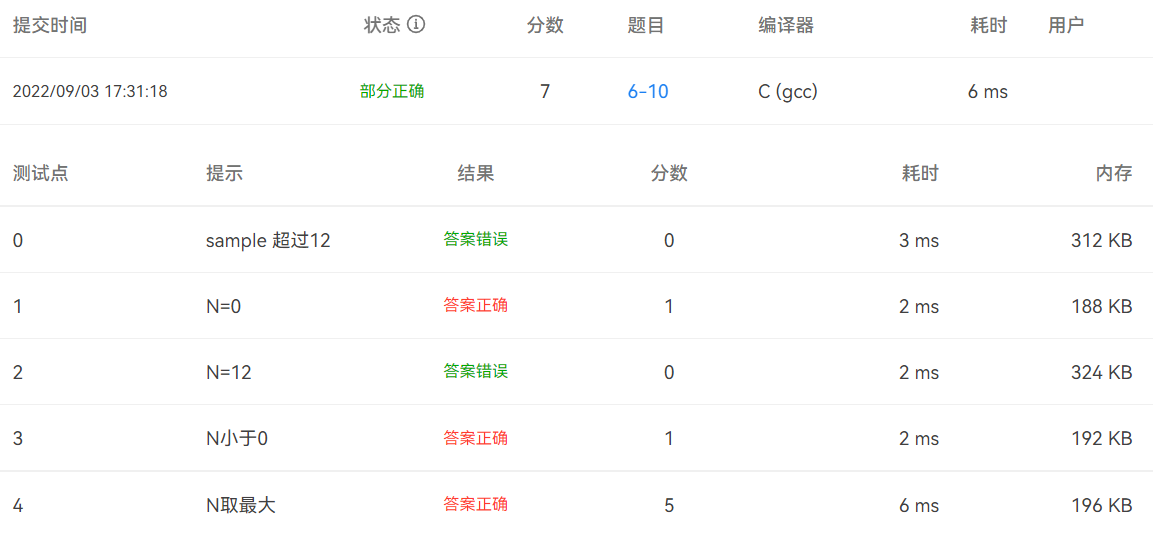
-
AC