實時降噪（Real-time Denoising）：Spatio-Temporal Filtering

目錄

空間濾波（Spatial Filtering）

基於距離的高斯濾波

僅考慮距離因素，會讓影像均勻變糊，損失了有用的高頻資訊。

雙邊濾波（Bilateral filtering）

額外考慮了顏色因素（基於認為顏色變化劇烈的地方是邊界，不應該貢獻太多權重）

\[w(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{\|I(i, j)-I(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)
\]

\(\sigma_d\) 和 \(\sigma_r\) 都是主觀設置的常量，即自己來決定各因素的權重影響。

聯合雙邊濾波（Joint Bilateral filtering）[2017]

SVGF（Spatio-Temporal Variance Guided Filter）[Schied 2017] = 聯合雙邊濾波 + 時域濾波

聯合雙邊濾波（Joint Bilateral filtering）：充分利用 G-buffer 的各種屬性作為參考，控制空間濾波的核和權重

問題關鍵實際就是在判斷高頻資訊屬於雜訊還是影像資訊，而 G-buffer 是光柵化過程生成的完全沒有雜訊，因此作為濾波的指導是非常有用的。

考慮的點有：

  • 聯合考慮深度差異和法線（不能簡單的單純考慮深度差異）
    • 實際上就是考慮沿平面的深度差距
\[w_{z}=\exp \left(-\frac{|z(p)-z(q)|}{\sigma_{z}|\nabla z(p) \cdot(p-q)|+\epsilon}\right)
\]

image-20220819151451027

  • 法線的差異
    • 求出來的值有可能是負值，因此使用了 max() 函數
    • \(\sigma_n\) 是為了更突出法線變化
\[w_{n}=\max (0, n(p) \cdot n(q))^{\sigma_{n}}
\]

註：如果使用法線貼圖，使用法線貼圖變換前的法線。

image-20220819151514218

  • 亮度的差異（兩點顏色間的灰度差距）：差異過大則認為兩點位置靠近邊界，貢獻不應過大
    • 由於雜訊可能會出現干擾，因此需要 variance 指導
\[w_{l}=\exp \left(-\frac{\left|l_{i}(p)-l_{i}(q)\right|}{\sigma_{l} \sqrt{g_{3 \times 3}\left(\operatorname{Var}\left(l_{i}(p)\right)\right)}+\epsilon}\right)
\]

方差 Var 的計算：

  1. 計算需要濾波的點 7×7 範圍內的方差
  2. 按時域的方法，通過motion vector計算上一幀對應像素的方差，並計算平均（相當於按時域濾波了，將方差變得時域上平滑）
  3. 再在周圍 3×3 的區域內做空間的平均濾波

image-20220819151540270

最後綜合權重就可以計算為 \(w=w_z*w_n*w_l\)

一些改進及優化

加速 filtering: 可分離的高斯濾波

如果濾波核採用高斯函數的形式，得益於 2D 高斯可分離成水平垂直兩次 1D 高斯濾波的特性，可以對影像進行一個水平方向的 1D 高斯濾波 pass 和一個垂直方向的 1D 高斯濾波 pass，將時間複雜度從 \(O(mnk^2)\) 降到 \(O(2mnk)\)

\(m,n\) 代表影像長寬，\(k\) 代表方形濾波核邊長

\[G_{2 D}(x, y)=G_{1 D}(x) \cdot G_{1 D}(y)$​
\]

\[\iint F\left(x_{0}, y_{0}\right) G_{2 D}\left(x_{0}-x, y_{0}-y\right) \mathrm{d} x \mathrm{~d} y=\int\left(\int F\left(x_{0}, y_{0}\right) G_{1 D}\left(x_{0}-x\right) \mathrm{d} x\right) G_{1 D}\left(y_{0}-y\right) \mathrm{d} y
\]

加速 filtering: a-trous wavelet

而對於非高斯函數形式或者說更複雜的濾波核（例如聯合雙邊濾波核），就很難像單純的高斯核那樣可分離成兩個 1D Pass。這時候就可能需要 a-trous wavelet 方法來優化較大濾波範圍的原始2D濾波

a-trous wavelet：採用多 pass 的方式，每個 pass 使用 3×3 或 5×5 的小濾波範圍但逐漸增加取樣間隔。

具體來說，第 \(i\) 個 pass 的取樣間隔將為 \(2^{i-1}-1\)（相鄰兩個 pass 的取樣間隔相差 \(2^i\)）

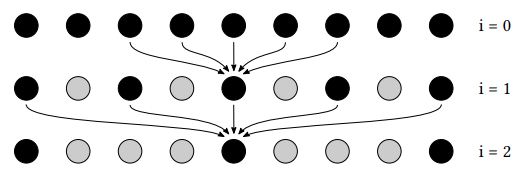
時間複雜度 \(O(mnk^2)\) 降到 \(O(mn\cdot 5^2\cdot log_2{k})\)，只是需要額外的紋理用來寫入前一個 pass 的輸出（中間結果）。因此對於超大範圍的濾波，使用 a-trous wavelet 方法增加的寫入開銷還是遠遠比節省的取樣開銷小。

例如：本來一個 64×64 的 2D 濾波，在該方法中就會變成使用 5 個 Pass，每個 Pass 做 5×5 的 2D 濾波。因為在使用第五個 pass 時，取樣間隔為 15，也就是說取樣總跨度為 15*4+5 = 65，即 65×65 的濾波範圍，與 64×64 已經非常相似。

jittering

結合 jittering 來進行子取樣，進一步減少取樣數。

outliers removal

可以根據設置的閾值 max radiance 限制或者根據 variance 去 clamp 掉顏色差異較大的 pixel（例如一些亮點）

當然直接粗暴的剔除這些亮點可能會導致能量不守恆，但是最高效的減少 firefly 方法就是如此。

img

// Ray Tracing Gems Chapter 17
vec3 fireflyRejectionClamp(vec3 radiance, vec3 maxRadiance)
{
    return min(radiance, maxRadiance);
}
// Ray Tracing Gems Chapter 25
vec3 fireflyRejectionVariance(vec3 radiance, vec3 variance, vec3 shortMean, vec3 dev)
{
    vec3 dev = sqrt(max(1.0e-5, variance));
    vec3 highThreshold = 0.1 + shortMean + dev * 8.0;
    vec3 overflow = max(0.0, radiance - highThreshold);
    return radiance - overflow;
}

時域濾波（Temporal Filtering）

Temporal Filtering

簡單地說，就是想找到本幀某 pixel 對應上一幀哪個 pixel 然後進行線性混合，這樣就可以通過時序來增加取樣數，讓當前影像雜訊更加小些。

當然，也不能簡單地按照相同的螢幕 uv 坐標來直接混合；因為物體和攝像機隨時都會發生移動等變化，這時候就需要藉助 motion vector 來找到上幀對應的準確螢幕位置。

具體步驟：

  1. back projection（後向投影）：用於計算出 pixel 在兩幀之間的 motion vector（即要找到本幀某 pixel 對應上一幀哪個 pixel）

  2. 求出當前幀 pixel 的世界坐標（如果保存了G-buffer可以直接取值用；如果沒有保存，通過逆視口變換、逆VP變換得到）

  3. 將當前幀的 pixel 世界坐標乘本幀的變換矩陣的逆矩陣 \(T^{-1}_i\)，再乘上一幀的變換矩陣 \(T_{i-1}\)，從而得到上一幀這個 pixel 對應的世界坐標。

  4. 將上一幀的世界坐標經上一幀 \(VP\) 和視口變換得到上一幀的 pixel 螢幕位置

  5. 本幀 pixel 的顏色與上一幀對應位置的 pixel 的顏色進行線性混合：

\[\bar{C}^{(i)}=\operatorname{Filter}\left[\tilde{C}^{(i)}\right]
\]

\[\bar{C}^{(i)}=\alpha \bar{C}^{(i)}+(1-\alpha) C^{(i-1)}​
\]

~ 為未空間濾波，- 為已空間濾波；\(\alpha\) 一般為 0.1~0.2

所需存儲的主要歷史資訊：

  • 上一幀的 color buffer（一般來說 temporal 混合的都是 color）
  • 上一幀的所有物體的變換矩陣（transforms）

問題：

  • 鏡頭的第一幀，或光源突變的情況無法處理
  • 螢幕空間資訊不足：比如螢幕外的點進入了螢幕內（由於時域濾波基於螢幕空間）
  • 被遮擋的物體突然出現（本質還是螢幕空間問題）
  • 由於世界空間幾何位置沒有變化（從而motion vector沒有變化），導致 shadow 、reflection 等滯後的現象

一些改進及優化

clamping

使用 clamp 來避免 color 發生太大的變化，減輕鬼影現象。

  1. 對本幀 \(x_i\) 鄰域計算均值 \(\mu\) 和方差 \(\sigma\) （可以在做空間濾波時順便求出來，基本無開銷）
  2. 對本幀 \(x_i\) 進行 reprojection 得到對應上幀的位置 \(x^o_{i-1}\)
  3. 對 \(x^o_{i-1}\) 的 color 進行 clamp，clamp 在 \([\mu-\sigma,\mu+\sigma]\)
  4. 混合本幀 \(x_i\) 的 color 和上幀的 clamp color

detection

可以通過檢測某些條件來決定是否混合上一幀的結果，比如：

  • 可以判斷前後兩幀 motion vector 對應的 pixel 對應的物體是否為一個物體：如果不是同一物體，混合係數 \(\alpha\) 設為 0

    該方法需要額外存儲歷史幀的 id buffer

混合 irradiance 而非 color

前面提到的 temporal 基本都是在混合 color，但實際上混合 irradiance 的效果更好：因為 irradiance 與不同著色點的法線無關，它相比 color 更加平滑。

  • 記錄歷史幀 normal + irradiance：
    • 假設表面都是 diffuse ，因此只需存儲半球中心對應法線，而無需存儲方向相關的 irradiance 強度資訊
    • 螢幕空間本幀法線對應半球範圍與歷史幀法線對應半球範圍的重合比例決定歷史幀 irradiance 的 temporal 混合權重
    • 僅可以支援 diffuse

image-20220810153654064

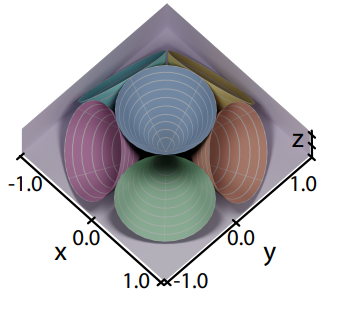
  • 記錄歷史幀 normal + 6 個 irradiance：
    • 使用 6 個圓錐立體角來粗略表示在不同方向上的 irradiance 強度資訊（代表了 shading point 在這個立體角範圍接受的 radiance 的總和）
    • 可以支援 diffuse + specular

image-20220810153714299

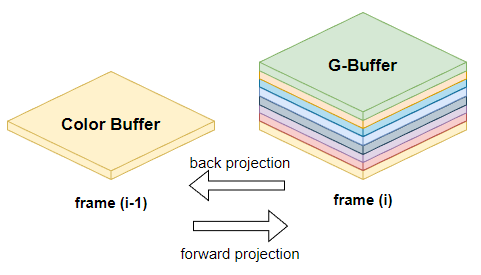
A-SVGF [2018]

改進了 SVGF 的 temporal filtering 操作，先計算出 temporal gradient（時域梯度，可以理解成表示 shading point 在兩幀之間著色變化的程度），再根據此計算出每 pixel 做 temporal filtering 時的混合係數，而不非使用一個固定的混合係數，增強了結果的時序穩定性。

估計 temporal gradient

temporal 樣本的復用需要進行 reprojection，而 reprojection 有兩種方法：

  • back projection（反向投影）就是把本幀的 sample 投影到先前幀的位置：\(\overleftarrow{G}_{i, j}\)
  • forward projection（前向投影）先前幀的樣本投影到本幀：\(\vec{G}_{i-1, j}\)

定義第 i 幀的第 j 個像素的表面取樣表示為 \(G_{i,j}\)

以前計算 motion vector 時，我們往往是使用 back projection，而在計算 temporal gradient 時我們使用了 forward projection。

原因是本幀擁有的資訊（G-Buffer）往往比上幀擁有的資訊（幾乎只有個 Color Buffer）多，使用 forward projection 的時候就可以有更多參考資訊。

image-20220812160655900

介紹完上面前置的知識後，這裡定義 \(f\) 為著色函數，那麼 temporal gradient 則可以表示為：

\[\delta_{i, \vec{j}}=f_{i}\left(\vec{G}_{i-1, j}\right)-f_{i-1}\left(G_{i-1, j}\right)
\]

在上一幀渲染的收尾階段時，我們可以將螢幕分成若干個 tile，每個 tile 抽取一個 pixel \(G_{i-1}\) 作為歷史樣本，並將歷史樣本列表傳遞給本幀（也就是它的下一幀）。

在本幀，我們對歷史樣本列表的所有樣本進行 forward projection，找到它們對應在本幀的位置 \(\vec{G}_{i-1, j}\)

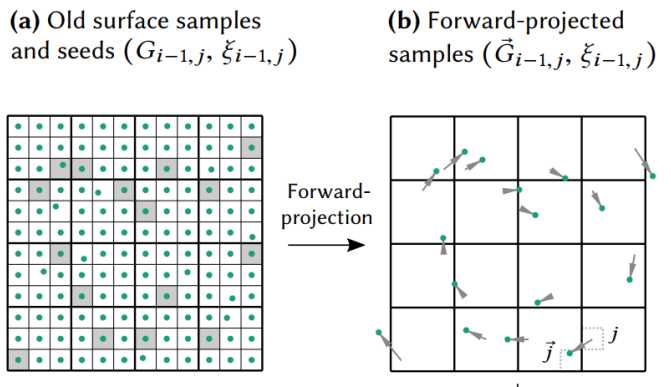
image-20220812162528592

也就是說上一幀保留的資訊有：Color Buffer + 物體 transforms + 歷史樣本列表（每個樣本只需要帶 position 屬性）

雖然對歷史所有 pixels 作 forward projection 能獲得品質更好的 temporal gradient，但這樣需要保留的歷史資訊就又多了個 position buffer，開銷增大太多不值得；而稀疏的歷史 pixels 樣本足以在低開銷的情況下估計並重建出夠用的 temporal gradient（無需太精確）。

然後，對應本幀的位置 \(\vec{G}_{i-1, j}\) + 利用本幀的 G-Buffer 資訊並重新著色得到著色結果 \(f_{i}\left(\vec{G}_{i-1, j}\right)\)

同時，歷史樣本 \(G_{i-1}\) + 直接利用上一幀 color buffer 不做任何插值就能直接索引找到著色結果 \(f_{i-1}\left(G_{i-1, j}\right)\)

穩定的隨機取樣：我們還希望 temporal gradient 的方差不要過大（更少的雜訊），即對上一幀 \(G_{i-1}\) 的著色與 forward projection 後重新的著色之間的變化儘可能少受些雜訊干擾。

\[\begin{array}{r}
\operatorname{Var}\left(\delta_{i, \vec{j}}\right)=\operatorname{Var}\left(f_{i}\left(\vec{G}_{i-1, j}, \xi_{i, j}\right)\right)+\operatorname{Var}\left(f_{i-1}\left(G_{i-1, j}, \xi_{i-1, j}\right)\right) \\
-2 \cdot \operatorname{Cov}\left(f_{i}\left(\vec{G}_{i-1, j}, \xi_{i, \vec{j}}\right), f_{i-1}\left(G_{i-1, j}, \xi_{i-1, j}\right)\right)
\end{array}
\]

而這其中著色函數可能依賴於隨機數 \(\xi\)（例如path tracing 時隨機數會用於選擇取樣方向），我們就需要減少隨機數帶來的干擾。

為此，應當保持 forward projection 後也依賴於相同的隨機數，即令 \(\xi_{i-1,\vec{j}}:=\xi_{i-1, j}\)。這樣我們的歷史樣本還需要存儲上對應的隨機數種子 \(\xi_{i-1, j}\)

這樣，每個樣本位置對應的 temporal gradient 就能算出來了：\(\delta_{i, \vec{j}}=f_{i}\left(\vec{G}_{i-1, j}\right)-f_{i-1}\left(G_{i-1, j}\right)\)

接著，就需要根據這些稀疏的 temporal gradient 樣本，重建出稠密的 temporal gradient 2D texture

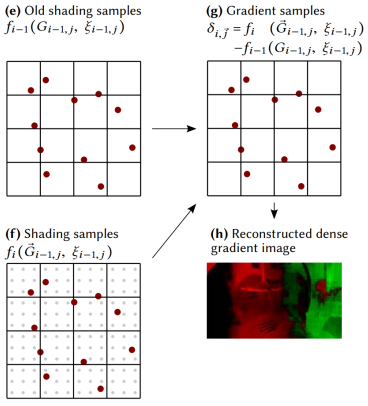
image-20220815112709801

重建 temporal gradient texture

稀疏的 temporal gradient 樣本可以看成是 image 中幾個特別亮的 texel，而我們可以利用聯合雙邊濾波的思路插值出來得到一張 temporal gradient 2D texture。

重建過程中幾個要點：

  • 初始 temporal gradient image 全部 texel 的梯度值設置為 0（全黑），除了 temporal gradient 樣本位置所在的 texel 是亮點（含有梯度值）

  • 濾波範圍需要大一些（因為樣本稀疏）

  • 需要多次迭代的聯合雙邊濾波：

    \[\hat{\delta}^{(k+1)}(p)=\frac{\sum_{q \in \Omega} h^{(k)}(p, q) w^{(k)}(p, q) \hat{\delta}^{(k)}(q)}{\sum_{q \in \Omega} h^{(k)}(p, q) w^{(k)}(p, q)}
    \]

個人的奇思妙想：不知道 temporal gradient 是否能再利用 temporal 思想，混合上一幀的 temporal gradient，來得到更加精確的 temporal temporal gradient（？）

根據 temporal gradient 控制 temporal 混合係數

已經有了重建好的 temporal gradient image，現在我們要控制時序濾波的因子了，首先加入標準化因子：

\[\Delta_{i, \vec{j}}=\max \left(f_{i}\left(\vec{G}_{i-1, j}, \xi_{i-1, j}\right), f_{i-1}\left(G_{i-1, j}, \xi_{i-1, j}\right)\right)
\]

因為空的層梯度設置為了 0，並使用了聯合雙邊濾波產生 \({\hat{\Delta}_{i}(p)}\)，我們定義密度和標準化歷史權重（該式意義在於讓 \(λ\) 小於等於 1）：

\[\lambda(p):=\min \left(1, \frac{\left|\hat{\delta}_{i}(p)\right|}{\hat{\Delta}_{i}(p)}\right)
\]

最後我們定義的 adaptive temporal 的混合係數為：

\[\alpha_{i}(p):=(1-\lambda(p)) \cdot \alpha+\lambda(p)
\]

更可靠的 Motion Vectors [2021]

motion vector 並不總是存在或無效，強行應用就會出現鬼影（隨著時間的推移，不合理的泄漏或陰影滯後）：

  • 背景中的靜態位置可能被前一幀的運動物體遮擋
  • 對於 shadow, glossy reflection 效果，motion vector 可能是錯誤的（如 receiver 具有長度為 0 的 motion vector，但投射到其上的 shadow 可能隨光源任意移動）

總的來說，感覺這篇 paper 實用的地方並不多，就是提供了除了額外三種 motion vector。然後 paper 並沒有結合這三種 motion vector 來使用，只是分別在三種場景單獨使用 shadow,glossy,dual 測測結果。

如果要落地的話，可以考慮：

  • 要不在 temporal filtering 過程中，通過權重來混合三種 motion vector 各自對應的 pixel
  • 要不在一條 pipeline 上使用至少三次 temporal filtering，其中三種方法分別處理 shadow，specular，final color 三種訊號

shadow motion vector

Percentage Closer Soft Shadows (PCSS) 需要 shading point 發射若干 rays 來檢測可以打到面光源的通過率（也就是 visibility），也就是說需要往 light 取樣多次。我們期望利用時序上（上一幀）的樣本來增加 PCSS 的取樣數。

具體步驟：

  1. 在本幀，讓 shading point 投射一條 shadow ray 打到 light 上，並記下可能穿過 blocker 的點 \(b_i\) 和打到光源面上的點 \(l_i\)
  2. back projection：\(b_i\) 通過本幀 blocker 的逆變換 \(T^{-1}_i\) 和上一幀 blocker 的變換 \(T_{i-1}\) 得到 \(b_{i-1}\) ；同理 \(l_i\) 也能得到 \(l_{i-1}\)
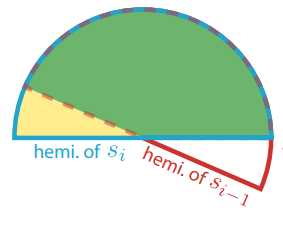
  3. 以 \(s_i\) 和其法線 \(n_{s_i}\) 構造一個無限長平面，然後將 \(l_{i-1}\) 與 \(b_{i-1}\) 連成線後相交於該平面，算出該相交點 \(s_{i-1}\)

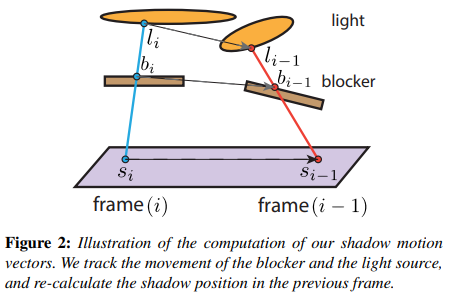
image-20220811110446632

  1. 把 \(s_{i-1}\) 投影到本幀 camera 的螢幕中，並得到螢幕 uv 後根據 depth buffer 重建出實際被看到的 shading point 位置 \(s^V_{i-1}\)，也就是說計算出的 motion vector = \(s^V_{i-1}-s_{i-1}\)

  2. 此外，當 \(s^V_{i-1}\) 與 \(s_i\) 真的如假設那樣在同一平面，那麼這個 motion vector 極大概率是準確的，也就是說取樣歷史幀時可以參考 \(s^V_{i-1}\)；否則，就不應該過多參考 \(s^V_{i-1}\)

    為此，可以根據 \(\theta\) （\(s_i\) 法線與 motion vector 的夾角）來實現加權的 temporal 混合，這樣當 \(\theta\) 與 \(\frac{\pi}{2}\) 相差很大時就可以相當於拒絕取樣歷史幀樣本。

    weight：

\[ \alpha^{V}=1-G\left(\theta-\frac{\pi}{2} ; 0,0.1\right) \cdot(1-\alpha)
\]

\(cos \theta = \frac{n_{s_i} \cdot (s^V_{i-1}-s_i)}{|s^V_{i-1}-s_i|}\)

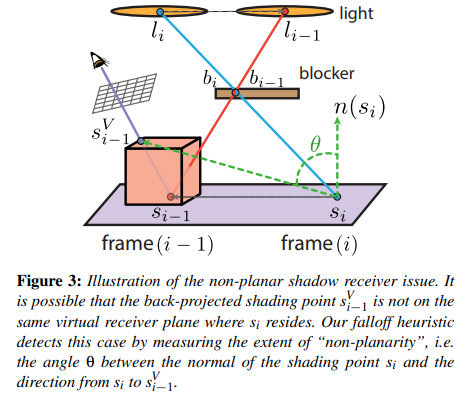
image-20220811110500447

不過取樣結果是稍微 noisy 的，因此還需要一些 clean-up filter。

個人想法：直接對 color 訊號處理可能並不準確，而如果對單純的 shadow 訊號處理會更好。

glossy motion vector

對於 glossy motion vector，也是類似思想。我們期望利用時序上（上一幀）的樣本來增加 glossy reflection 的取樣數。

具體步驟：

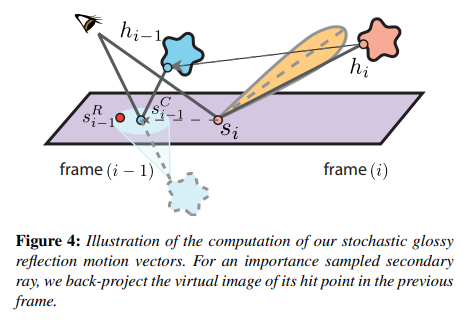
  1. 在本幀，讓 shading point 根據 brdf importance sampling 來生成一條 ray 並打到某個 mesh 上，並記下 hit point \(h_i\)
  2. back projection：\(h_i\) 通過本幀 mesh 的逆世界變換 \(T^{-1}_i\) 和上一幀 mesh 的世界變換 \(T_{i-1}\) 得到 \(h_{i-1}\)
  3. 以 \(s_i\) 和其法線 \(n_{s_i}\) 構造一個無限長平面，然後將 \(h_{i-1}\) 於該平面翻轉（類似形成一個倒置的虛像），並連接 camera point，算出與該平面的相交點 \(s^C_{i-1}\)

因為 glossy lobe 的中心方向是最強烈的反射方向，因此可以假設退化成純鏡面反射方向，就能得到反射率最高的 shading point

  1. 以 \(s^C_{i-1}\) 為中心，鄰近的 shading point 都可以作為取樣的參考（根據 \(s^C_{i-1}\) 的材質 roughness 程度決定半徑），並且對這一圈的樣本按高斯分布的方式去加權取樣結果作為歷史幀的 color
  2. 類似 shadow motion vector，利用 \(\theta\) 檢測共平面的程度，當 \(\theta\) 與 \(\frac{\pi}{2}\) 相差很大時就可以相當於拒絕取樣歷史幀樣本

image-20220811115235954

個人想法：直接對 color 訊號（包含 diffuse + specular）處理可能並不準確，而如果對單純的 specular 訊號處理會更好。

dual motion vector

假設在本幀 pixel \(x_i\) 可見，而在上一幀它被 occluder \(y\) 遮擋住了。

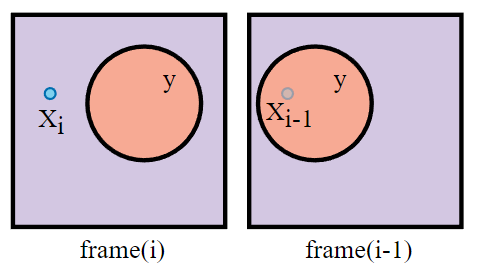
image-20220829010957764

傳統 motion vector ：

  1. 對本幀 \(x_i\) 進行 reprojection 得到對應上幀的位置 \(x^o_{i-1}\)（但其實 \(x^o_{i-1}\) 是投影在了上幀的 occluder \(y\) 上，因此得到的上幀 color 是 occluder \(y\) 的 color）
  2. 強行混合本幀 \(x_i\) 的 color 和上幀的 color，這也是造成鬼影的一大原因

dual motion vectors：基於假設要渲染的 pixel 和 occluder 的相對位置不變。

  1. 對本幀 \(x_i\) 進行 back projection 得到對應上幀的位置 \(y\)
  2. 再將上幀 \(y\) 進行 forward projection （需要藉助歷史 id buffer）得到對應本幀的位置 \(z\)
  3. 計算相對位移 \(offset = x_i-z\)
  4. 那麼最終找到的對應上幀位置便是 \(x^o_{i-1} = y + offset\)
  5. 混合本幀 \(x_i\) 的 color 和上幀 \(x^o_{i-1}\)

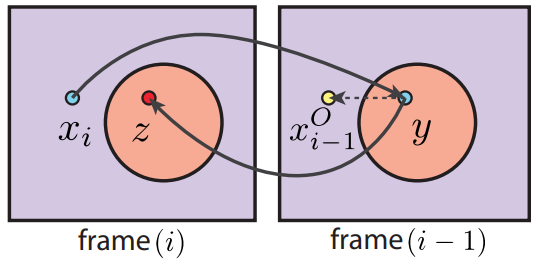
image-20220810143838836

對於沒有遮擋物的案例來說，\(offset\) 往往是 0，即用了 dual motion vectors 會退化成傳統 motion vector：

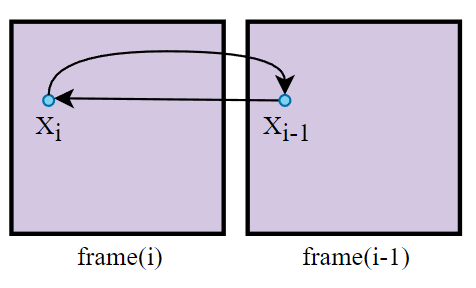
image-20220829011154517

為什麼要假設渲染的 pixel 和 occluder 的相對位置不變？

這是因為，根據相對位置算出來的上幀位置雖然一般不是該 pixel 以前的真正位置，但是該位置很大概率是位於與該 pixel 處在同一平面的鄰近位置，而這些位置得到的 color 和 pixel 得到的 color 就很大相似度，有一定參考價值。

本方法所需存儲的主要歷史資訊：

  • color buffer
  • id buffer
  • 物體 transforms

個人想法：既然有歷史 id buffer，其實這個方法在最後的步驟也可以結合 detection 方法，通過比較 pixel 的歷史 id 和當前 id 來進一步規避邊緣情況。

參考

Tags:

VirMach 便宜 VPS

QNews

QNews