C++ 漫談哈夫曼樹

2022 年 8 月 19 日
筆記
C++, C++編程之美

1. 前言

什麼是哈夫曼樹？

把權值不同的n個結點構造成一棵二叉樹，如果此樹滿足以下幾個條件：

此 n 個結點為二叉樹的葉結點 。
權值較大的結點離根結點較近，權值較小的結點離根結點較遠。
該樹的帶權路徑長度是所有可能構建的二叉樹中最小的。

則稱符合上述條件的二叉樹為最優二叉樹，也稱為哈夫曼樹(Huffman Tree)。

構建哈夫曼樹的目的是什麼？

用來解決在通訊系統中如何使用最少的二進位位編碼字元資訊。

本文將和大家聊聊哈夫曼樹的設計思想以及構建過程。

2. 設計思路

哈夫曼樹產生的背景：

在通訊系統中傳遞一串字元串文本時，需要對這一串字元串文本資訊進行二進位編碼。編碼時如何保證所用到的bit位是最少的，或保證整個編碼後的傳輸長度最短。

現假設字元串由ABCD 4個字元組成，最直接的想法是使用 2 個bit位進行等長編碼，如下表格所示：

字元	編碼
`A`	`00`
`B`	`01`
`C`	`10`
`D`	`11`

傳輸ABCD字元串一次時，所需bit為 2位，當通訊次數達到 n次時，則需要的總傳輸長度為 n*2。當字元串的傳輸次數為 1000次時，所需要傳輸的總長度為 2000個bit。

使用等長編碼時，如果傳輸的報文中有 26 個不同字元時，因需要對每一個字元進行編碼，至少需要 5位bit。

但在實際應用中，各個字元的出現頻率或使用次數是不相同的，如A、B、C的使用頻率遠遠高於X、Y、Z。使用等長編碼特點是無論字元出現的頻率差異有多大，每一個字元都得使用相同的bit位。

哈夫曼的設計思想：

對字元串資訊進行編碼設計時，讓使用頻率高的字元使用短碼，使用頻率低的用長碼，以優化整個資訊編碼的長度。
基於這種簡單、樸素的想法設計出來的編碼也稱為不等長編碼。

哈夫曼不等長編碼的具體思路如下：

如現在要發送僅由A、B、C、D 4 個字元組成的報文資訊，A字元在資訊中佔比為 50%，B的佔比是 20%， C的佔比是 15%， D的佔比是10%。

不等長編碼的樸實思想是字元的佔比越大，所用的bit位就少，佔比越小，所用bit位越多。如下為每一個字元使用的bit位數：

A使用 1位bit編碼。
B使用 2 位 bit編碼。
C 使用 3 位 bit編碼。
D 使用 3 位 bit 編碼。

具體編碼如下表格所示：

字元	佔比	編碼
`A`	`0.5`	`0`
`B`	`0.2`	`10`
`C`	`0.15`	`110`
`D`	`0.1`	`111`

如此編碼後，是否真的比前面的等長編碼所使用的總bit位要少？

計算結果=0.5*1+0.2*2+0.15*3+0.1*3=1.65。

先計算每一個字元在報文資訊中的佔比乘以字元所使用的bit位。

然後對上述每一個字元計算後的結果進行相加。

顯然，編碼ABCD只需要 1.65 個bit ，比等長編碼用到的2 個 bit位要少。當傳輸資訊量為 1000時，總共所需要的bit位=1.65*1000=1650 bit。

哈夫曼編碼和哈夫曼樹有什麼關係？

因為字元的編碼是通過構建一棵自下向上的二叉樹推導出來的，如下圖所示：

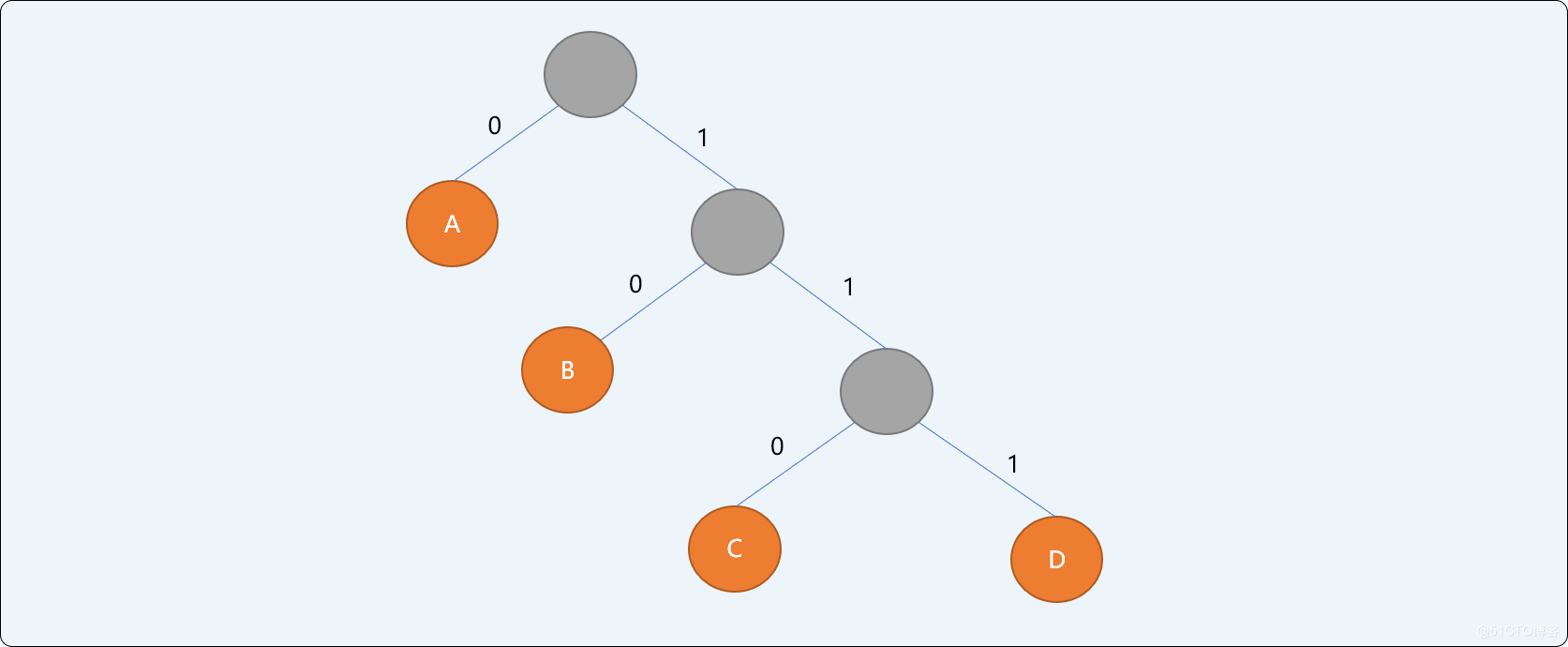
哈夫曼樹的特點：

資訊結點都是葉子結點。
葉子結點具有權值。如上二叉樹，A結點權值為0.5，B結點權值為0.2，C結點權值為0.15，D結點權值為 0.1。
哈夫曼編碼為不等長前綴編碼（即要求一個字元的編碼不能是另一個字元編碼的前綴）。
從根結點開始，為左右分支分別編號0和1，然後順序連接從根結點到葉結點所有分支上的編號得到字元的編碼。

相信大家對哈夫曼樹有了一個大概了解，至於如何通過構建哈夫曼樹，咱們繼續再聊。

3. 構建思路

在構建哈夫曼樹之前，先了解幾個相關概念：

路徑和路徑長度：在一棵樹中，從一個結點往下可以達到的孩子或孫子結點之間的通路，稱為路徑。通路中分支的數目稱為路徑長度。若規定根結點的層數為1，則從根結點到第L層結點的路徑長度為L-1。
結點的權及帶權路徑長度：若將樹中結點賦給一個有著某種含義的數值，則這個數值稱為該結點的權。結點的帶權路徑長度為：從根結點到該結點之間的路徑長度與該結點的權的乘積。
樹的帶權路徑長度：樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和，記為WPL。

如有權值為{3,4,9,15}的 4 個結點，則可構造出不同的二叉樹，其帶權路徑長度也會不同。如下 3 種二叉樹中，B的樹帶權路徑長度是最小的。

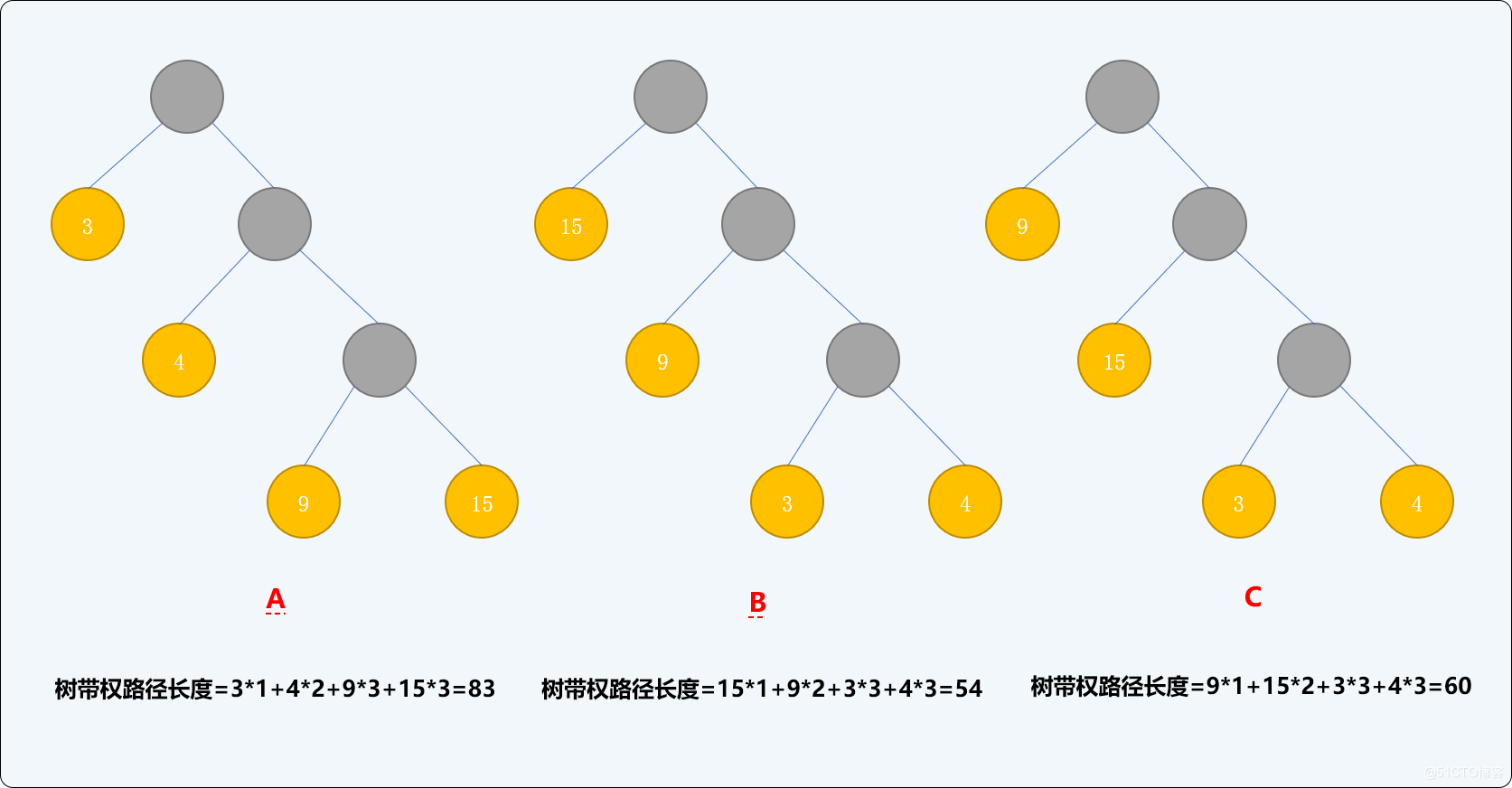
哈夫曼樹的構建過程就是要保證樹的帶權路徑長度最小。

那麼，如何構建二叉樹，才能保證構建出來的二叉樹的帶權路徑長度最小？

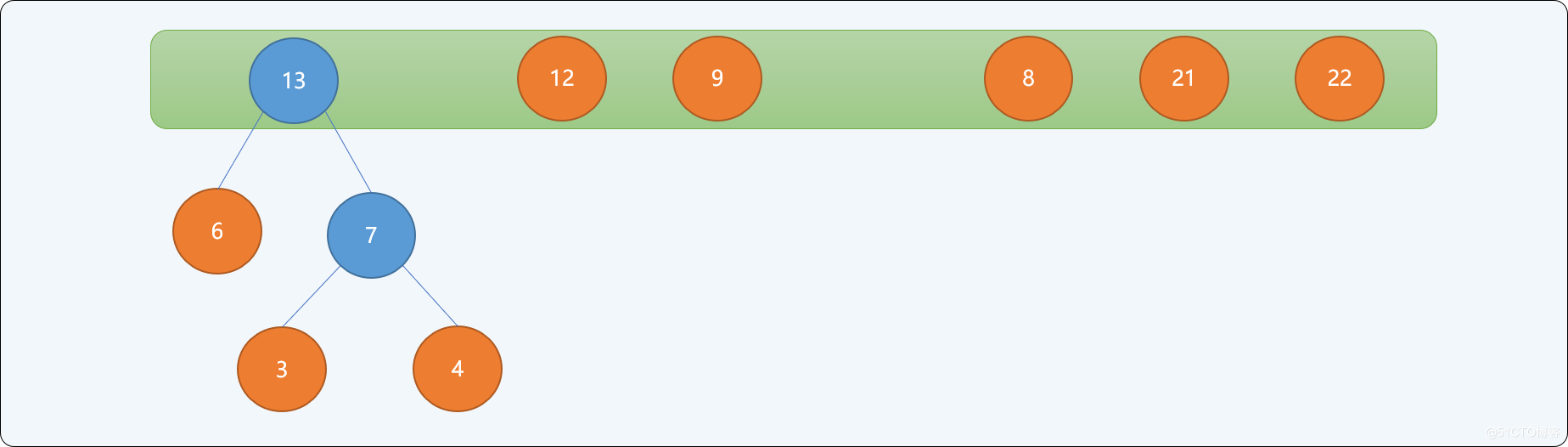
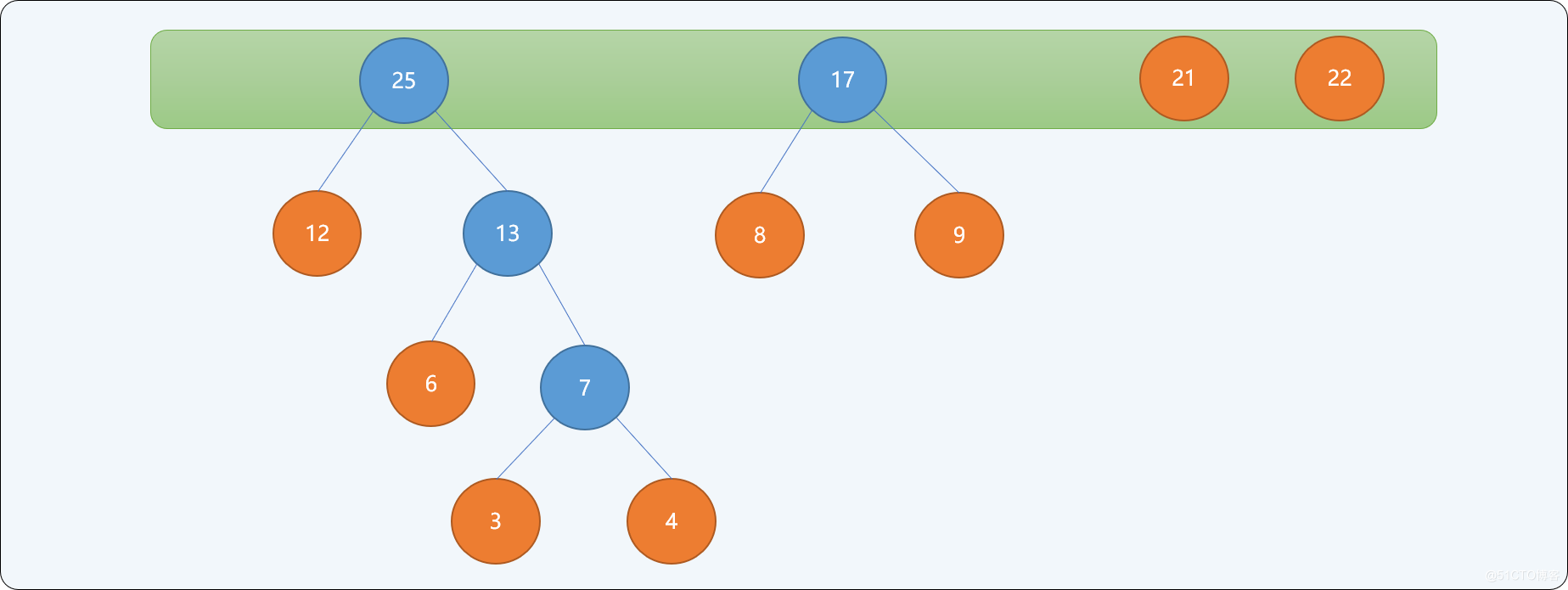
如有一字元串資訊由 ABCDEFGH 8個字元組成，每一個字元的權值分別為{3,6,12,9,4,8,21,22}，構建最優哈夫曼樹的流程：

以每一個結點為根結點構建一個單根二叉樹，二叉樹的左右子結點為空，根結點的權值為每個結點的權值。並存儲到一個樹集合中。

從樹集合中選擇根結點的權值最小的 2 個樹。重新構建一棵新二叉樹，讓剛選擇出來的2 棵樹的根結點成為這棵新樹的左右子結點，新樹的根結點的權值為 2 個左右子結點權值的和。構建完成後從樹集合中刪除原來 2個結點，並把新二叉樹放入樹集合中。

如下圖所示。權值為 3和4的結點為新二叉樹的左右子結點，新樹根結點的權值為7。

重複第二步，直到樹集合中只有一個根結點為止。

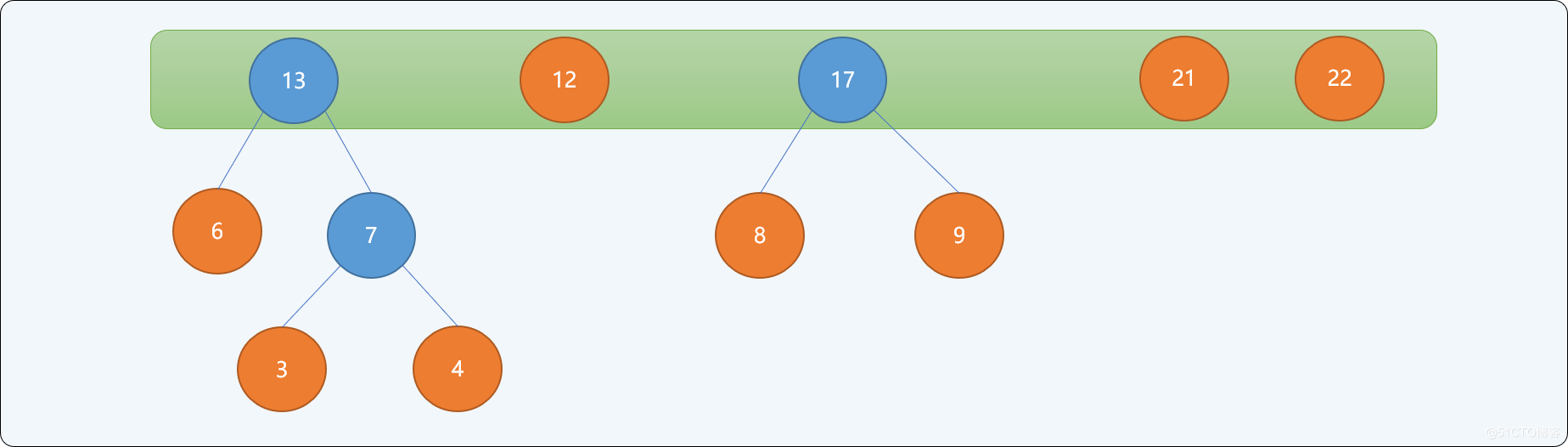
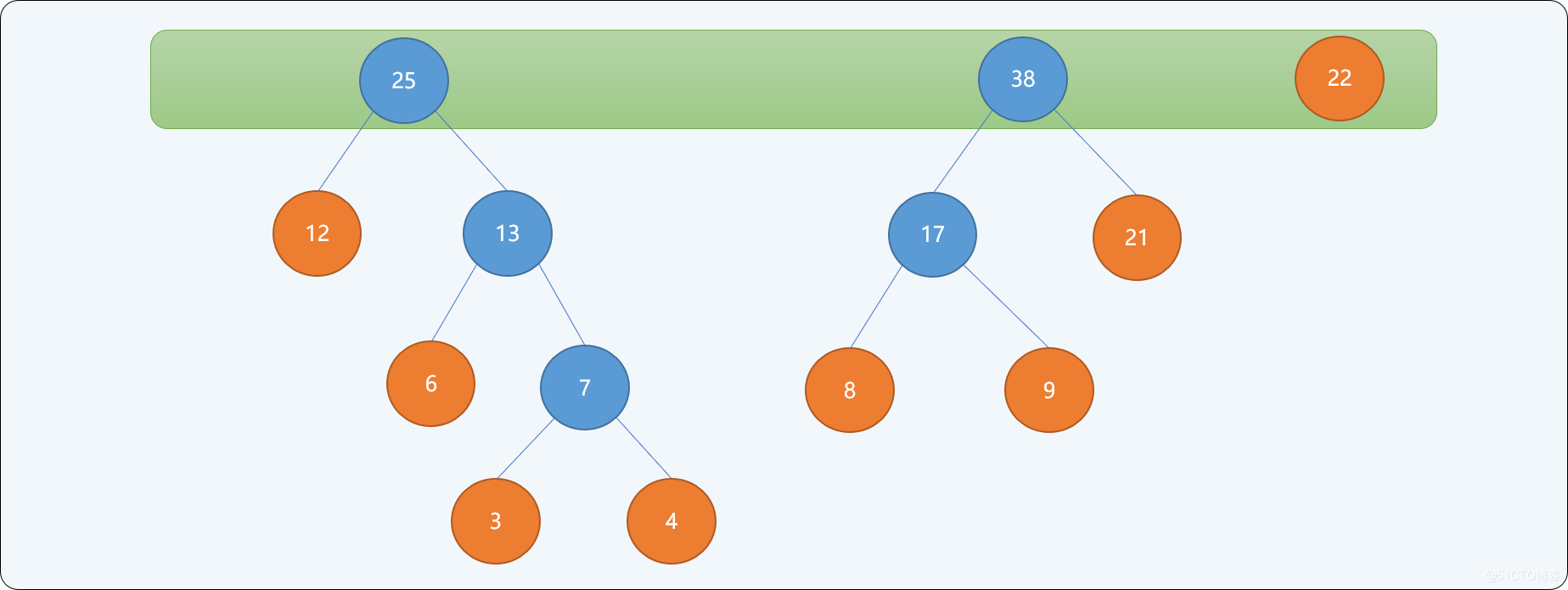
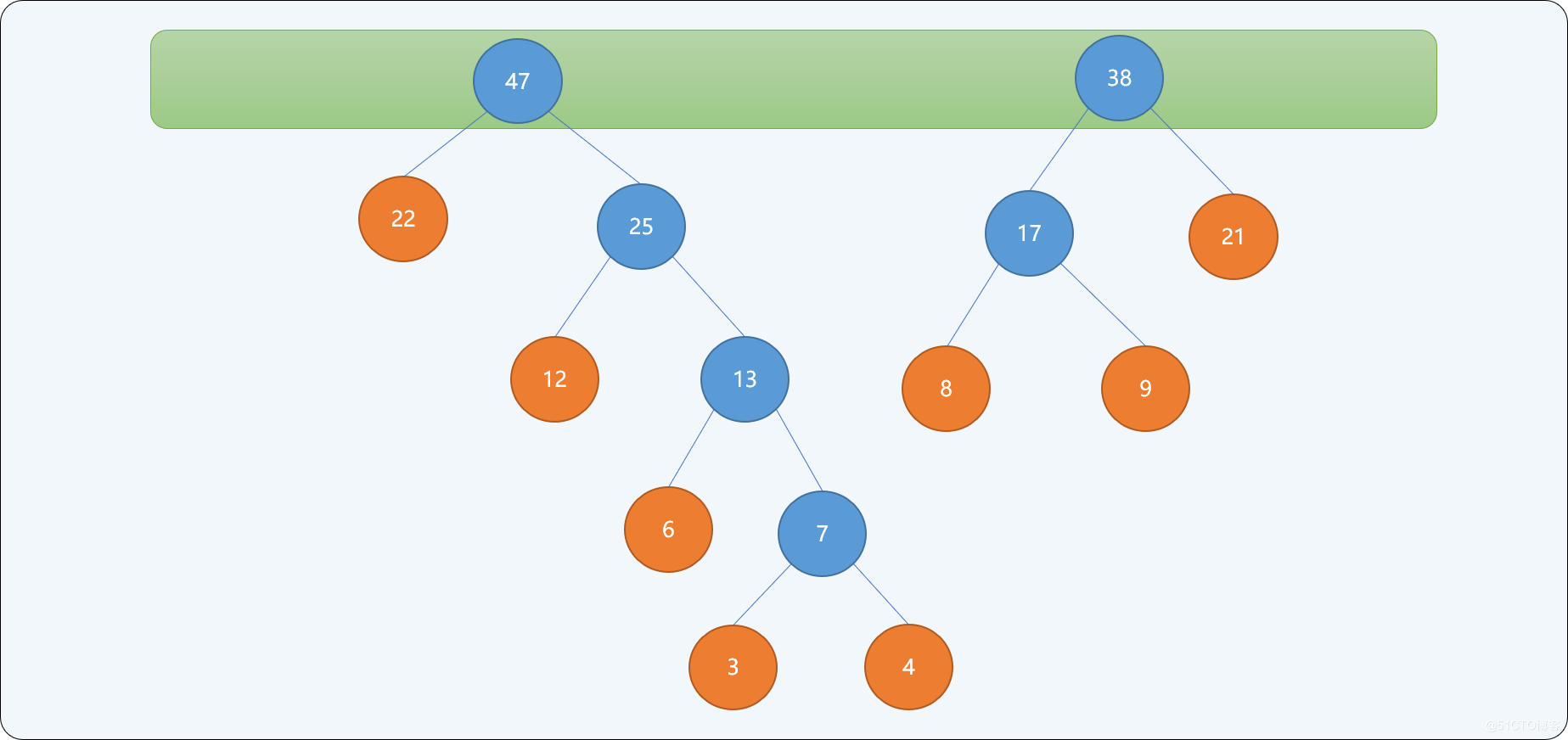
當集合中只存在一個根結點時，停止構建，並且為最後生成樹的每一個非葉子結點的左結點分支標註0，右結點分支標註1。如下圖所示：

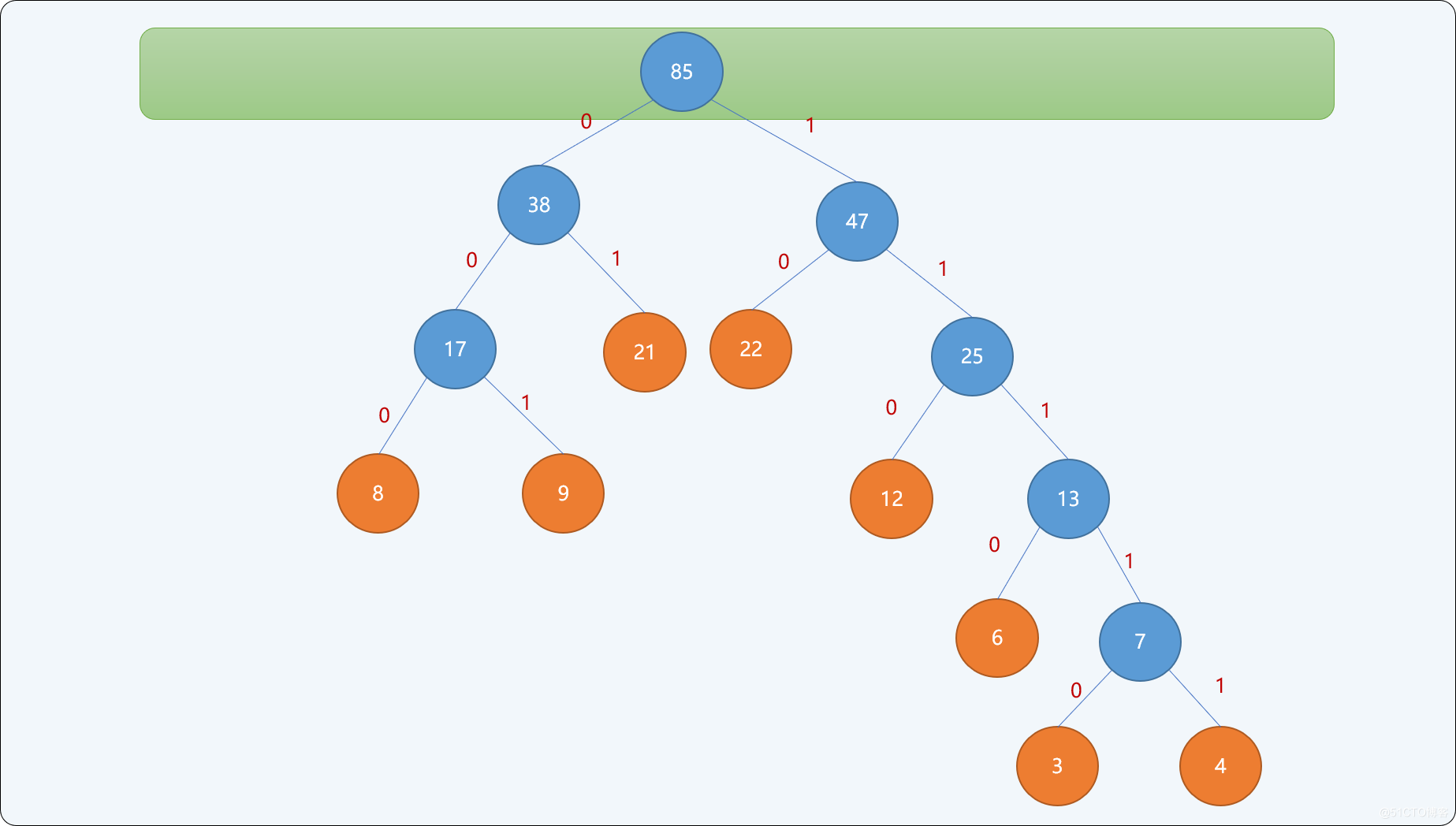
通過上述從下向上的思想構建出來的二叉樹，可以保證權值較小的結點離根結點較遠，權值較大的結點離根結點較近。最終二叉樹的帶權路徑長度： WPL=(3+4)*5+6*4+(8+9+12)*3+(21+22)*2=232 。並且此樹的帶權路徑長度是所有可能構建出來的二叉樹中最小的。

上述的構建思想即為哈夫曼樹設計思想，不同權值的字元編碼就是結點路徑上0和1的順序組合。如下表所述，權值越大，其編碼越小，權值越小，其編碼越大。其編碼長度即從根結點到此葉結點的路徑長度。

字元	權值	編碼
`A`	`3`	`11110`
`B`	`6`	`1110`
`C`	`12`	`110`
`D`	`9`	`001`
`E`	`4`	`11111`
`F`	`8`	`000`
`G`	`21`	`01`
`H`	`22`	`10`

4. 編碼實現

4.1 使用優先隊列

可以把權值不同的結點分別存儲在優先隊列（Priority Queue）中，並且給與權重較低的結點較高的優先順序（Priority）。

具體實現哈夫曼樹演算法如下：

把n個結點存儲到優先隊列中，則n個節點都有一個優先權Pi。這裡是權值越小，優先權越高。
如果隊列內的節點數>1，則：

從隊列中移除兩個最小的結點。
產生一個新節點，此節點為隊列中移除節點的父節點，且此節點的權重值為兩節點之權值之和，把新結點加入隊列中。
重複上述過程，最後留在優先隊列里的結點為哈夫曼樹的根節點（root）。

完整程式碼：

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
//樹結點
struct TreeNode {
	//結點權值
	float weight;
	//左結點
	TreeNode *lelfChild;
	//右結點
	TreeNode *rightChild;
    //初始化
	TreeNode(float w) {
		weight=w;
		lelfChild=NULL;
		rightChild=NULL;
    }
};
//為優先隊列提供比較函數
struct comp {
	bool operator() (TreeNode * a, TreeNode * b) {
        //由大到小排列
		return a->weight > b->weight; 
	}
};

//哈夫曼樹類
class HfmTree {
	private:
         //優先隊列容器
		priority_queue<TreeNode *,vector<TreeNode *>,comp> hfmQueue;
	public:
		//構造函數，構建單根結點樹
		HfmTree(int weights[8]) {
			for(int i=0; i<8; i++) {
				//創建不同權值的單根樹
				TreeNode *tn=new TreeNode(weights[i]);
				hfmQueue.push(tn);
			}
		}
		//顯示隊列中的最一個結點
		TreeNode* showHfmRoot() {
			TreeNode *tn;
			while(!hfmQueue.empty()) {
				tn= hfmQueue.top();
				hfmQueue.pop();
			}
			return tn;
		}
		//構建哈夫曼樹
		void create() {
             //重複直到隊列中只有一個結點
			while(hfmQueue.size()!=1) {
				//從優先隊列中找到權值最小的 2 個單根樹
				TreeNode *minFirst=hfmQueue.top();
				hfmQueue.pop();
				TreeNode *minSecond=hfmQueue.top();
				hfmQueue.pop();
				//創建新的二叉樹
				TreeNode *newRoot=new TreeNode(minFirst->weight+minSecond->weight);
				newRoot->lelfChild=minFirst;
				newRoot->rightChild=minSecond;
				//新二叉樹放入隊列中
				hfmQueue.push(newRoot);
			}
		}
		//按前序遍歷哈夫曼樹的所有結點
		void showHfmTree(TreeNode *root) {
			if(root!=NULL) {
				cout<<root->weight<<endl;
				showHfmTree(root->lelfChild);
				showHfmTree(root->rightChild);
			}
		}
		//析構函數
		~HfmTree() {
            //省略
		}
};

//測試
int main(int argc, char** argv) {
	//不同權值的結點
	int weights[8]= {3,6,12,9,4,8,21,22};
    //調用構造函數
	HfmTree hfmTree(weights);
    //創建哈夫曼樹
	hfmTree.create();
    //前序方式顯示哈夫曼樹
	TreeNode *root= hfmTree.showHfmRoot();
	hfmTree.showHfmTree(root);
	return 0;
}

顯示結果：

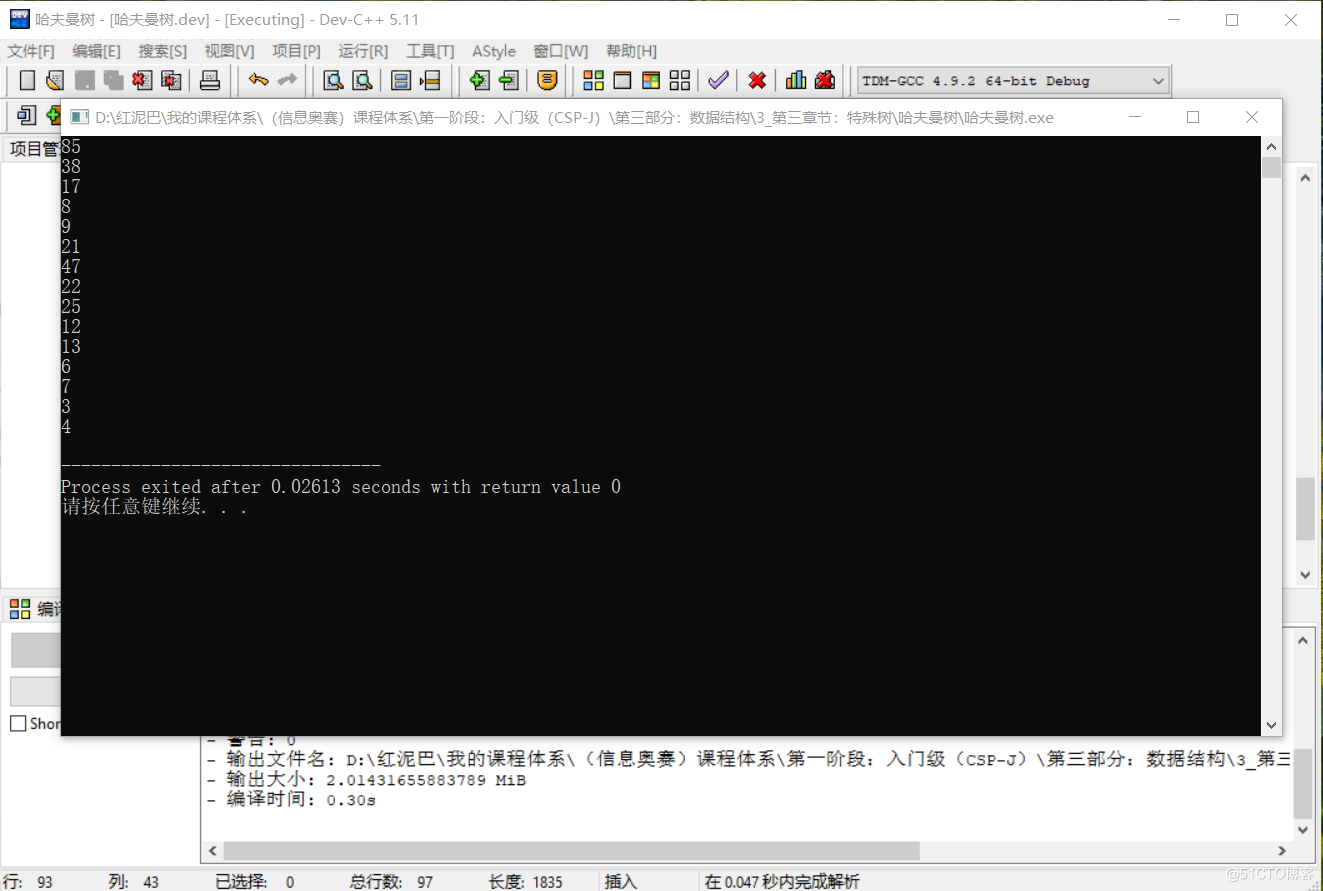
上述輸出結果，和前文的演示結果是一樣的。

此演算法的時間複雜度為O（nlogn）。因為有n個結點，所以樹總共有2n-1個節點，使用優先隊列每個循環須O（log n）。

4.2 使用一維數組

除了上文的使用優先隊列之外，還可以使用一維數組的存儲方式實現。

在哈夫曼樹中，葉子結點有 n個，非葉子結點有 n-1個，使用數組保存哈夫曼樹上所的結點需要 2n-1個存儲空間。其演算法思路和前文使用隊列的思路差不多。直接上程式碼：

#include <iostream>
using namespace std;
//葉結點數量
const unsigned int n=8;
//一維數組長度
const unsigned int m= 2*n -1;
//樹結點
struct TreeNode {
	//權值
	float weight;
	//父結點
	int parent;
	//左結點
	int leftChild;
	//右結點
	int rightChild;
};
class HuffmanTree {
	public:
		//創建一維數組
		TreeNode hfmNodes[m+1];
	public:
		//構造函數
		HuffmanTree(int weights[8]);
		~HuffmanTree( ) {

		}
		void findMinNode(int k, int &s1, int &s2);
		void showInfo() {
			for(int i=0; i<m; i++) {
				cout<<hfmNodes[i].weight<<endl;
			}
		}
};
HuffmanTree::HuffmanTree(int weights[8]) {
	//前2 個權值最小的結點
	int firstMin;
	int  secondMin;
	//初始化數組中的結點
	for(int i = 1; i <= m; i++) {
		hfmNodes[i].weight = 0;
		hfmNodes[i].parent = -1;
		hfmNodes[i].leftChild = -1;
		hfmNodes[i].rightChild = -1;
	}
	//前 n 個是葉結點
	for(int i = 1; i <= n; i++)
		hfmNodes[i].weight=weights[i-1];

	for(int i = n + 1; i <=m; i++) {
		this->findMinNode(i-1, firstMin, secondMin);
		hfmNodes[firstMin].parent = i;
		hfmNodes[secondMin].parent = i;
		hfmNodes[i].leftChild = firstMin;
		hfmNodes[i].rightChild = secondMin;
		hfmNodes[i].weight = hfmNodes[firstMin].weight + hfmNodes[secondMin].weight;
	}
}
void HuffmanTree::findMinNode(int k, int & firstMin, int & secondMin) {
	hfmNodes[0].weight = 32767;
	firstMin=secondMin=0;
	for(int i=1; i<=k; i++) {
		if(hfmNodes[i].weight!=0 && hfmNodes[i].parent==-1) {
			if(hfmNodes[i].weight < hfmNodes[firstMin].weight) { 
                  //如果有比第一小還要小的，則原來的第一小變成第二小
				secondMin = firstMin;
                  //新的第一小
				firstMin = i;
			} else if(hfmNodes[i].weight < hfmNodes[secondMin].weight)
			    //如果僅比第二小的小	
                 secondMin = i;
		}
	}
}

int main() {
	int weights[8]= {3,6,12,9,4,8,21,22};
	HuffmanTree huffmanTree(weights);
	huffmanTree.showInfo();
	return 1;
}

測試結果：

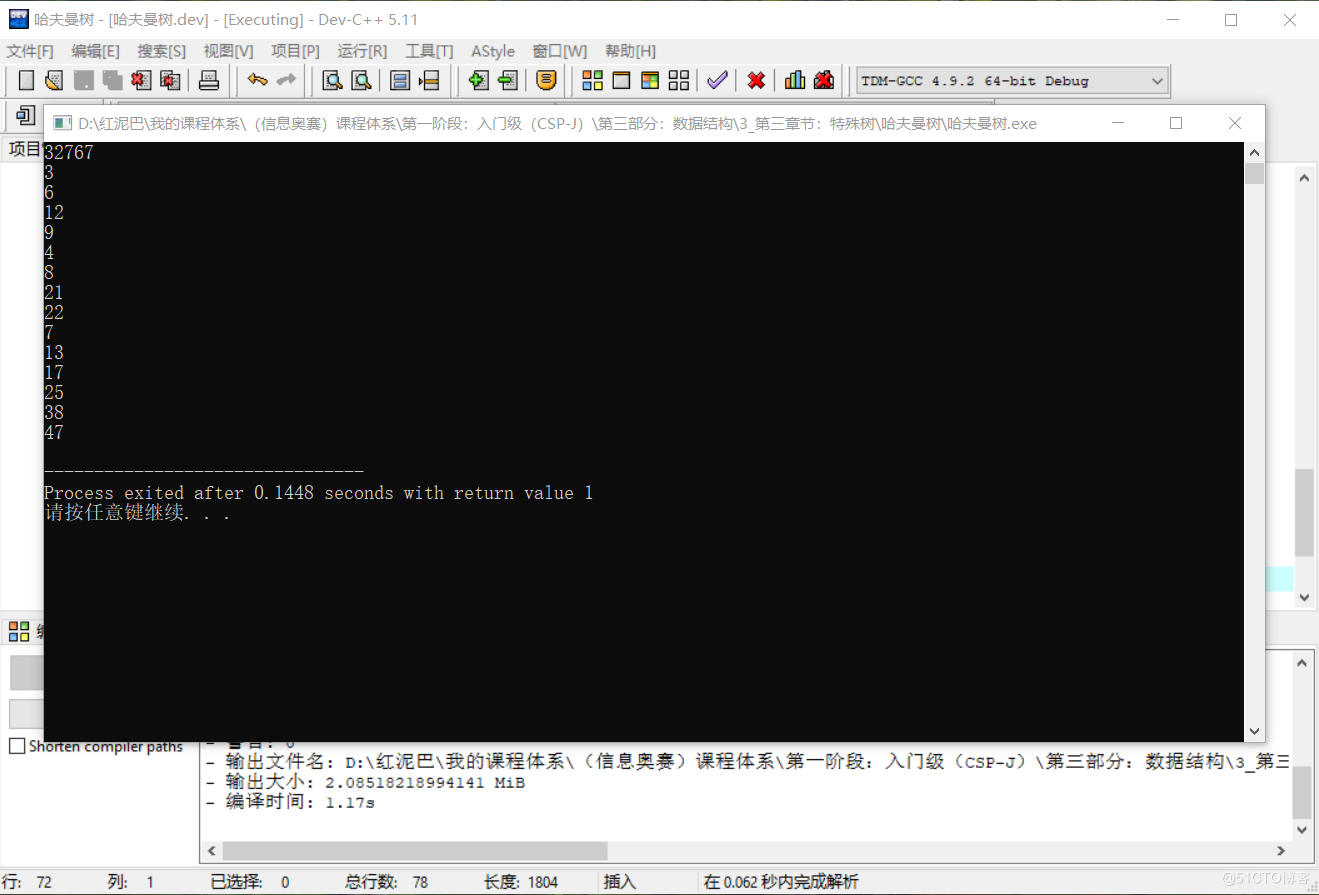
5. 總結

哈夫曼樹是二叉樹的應用之一，掌握哈夫曼樹的建立和編碼方法對解決實際問題有很大幫助。

Tags: C++ C++編程之美